Let g be the acceleration due to gravity at the earth's surface and K the rotational kinetic energy of the earth. Suppose the earth's radius decreases by 2%. Keeping all other quantities constant, then
g decreases by 2% and K decreases by 4%
g decreases by 4% and K decreases by 2%
g decreases by 4% and K decreases by 4%
g decreases by 4% and K increases by 4%
The correct Answer is:B
K=(1/2)Iω2=(1/2)(2/5)MR2ω2,
g=GM/R2
logg=logG+logM−2logR,(dg/g)×100=−2(dR/R)×100=−2×2%=−4%
Topper's Solved these Questions
- COMPETITION CARE UNITBOOK - ICSECHAPTER - COMPETITION CARE UNITEXERCISE - GRAVITATION
25 Videos
- COMPETITION CARE UNITBOOK - ICSECHAPTER - COMPETITION CARE UNITEXERCISE - PROPERTIES OF MATTER (ELASTICITY )
22 Videos
- COMPETITION CARE UNITBOOK - ICSECHAPTER - COMPETITION CARE UNITEXERCISE - UNIFORM CIRCULAR MOTION
25 Videos
- CIRCULAR MOTION BOOK - ICSECHAPTER - CIRCULAR MOTION EXERCISE - MODULE 2 (FROM ROTATIONAL KINETIC ENERGY , WORK ,POWER)
24 Videos
- DIMENSIONSBOOK - ICSECHAPTER - DIMENSIONSEXERCISE - SELECTED PROBLEMS (FROM CONVERSIONS OF ONE SYSTEMS OF UNITS INTO ANOTHER)
9 Videos
Similar Questions
Knowledge Check
If g be the acceleration due to gravity of the earth's surface, the gain is the potential energy of an object of mass m raised from the surface of the earth to a height equal to the radius R of the earth is
A(1/2) m g RB2 m g RCm g RD(1/4) m g R
If R is the radius of the earth and g the acceleration due to gravity on the earth's surface, the mean density of the earth is
View SolutionHow is the acceleration due to gravity on the surface of the earth related to its mass and radius ?
View SolutionBecause of the friction between the water in oceans with the earth's surface the rotational kinetic energy of the earth is continuously decreasing. If earth's angular speed decreases by 0.0016 rad/day in 100 years, find the average torque of the friction on the earth. Radius of the earth is 6400 km and its mass is 6.0×1024kg.
View SolutionIf ge,gh and gd be the acceleration due to gravity at earth’s surface, a height h and at depth d respectively . Then:
View SolutionIf g is the acceleration due to gravity on the surface of the earth , its value at a height equal to double the radius of the earth is
View SolutionThe ratio of acceleration due to gravity at a height 3 R above earth's surface to the acceleration due to gravity on the surface of earth is
(R = radius of earth)
View SolutionSuppose the acceleration due to gravity at earth's surface is 10ms−2 and at the surface of Mars it is 4.0ms−2. A passenger goes from the earth to the mars in a spaceship with a constant velocity. Neglect all other object in sky. Which part of figure best represent the weight (net gravitational force) of the passenger as a function of time?
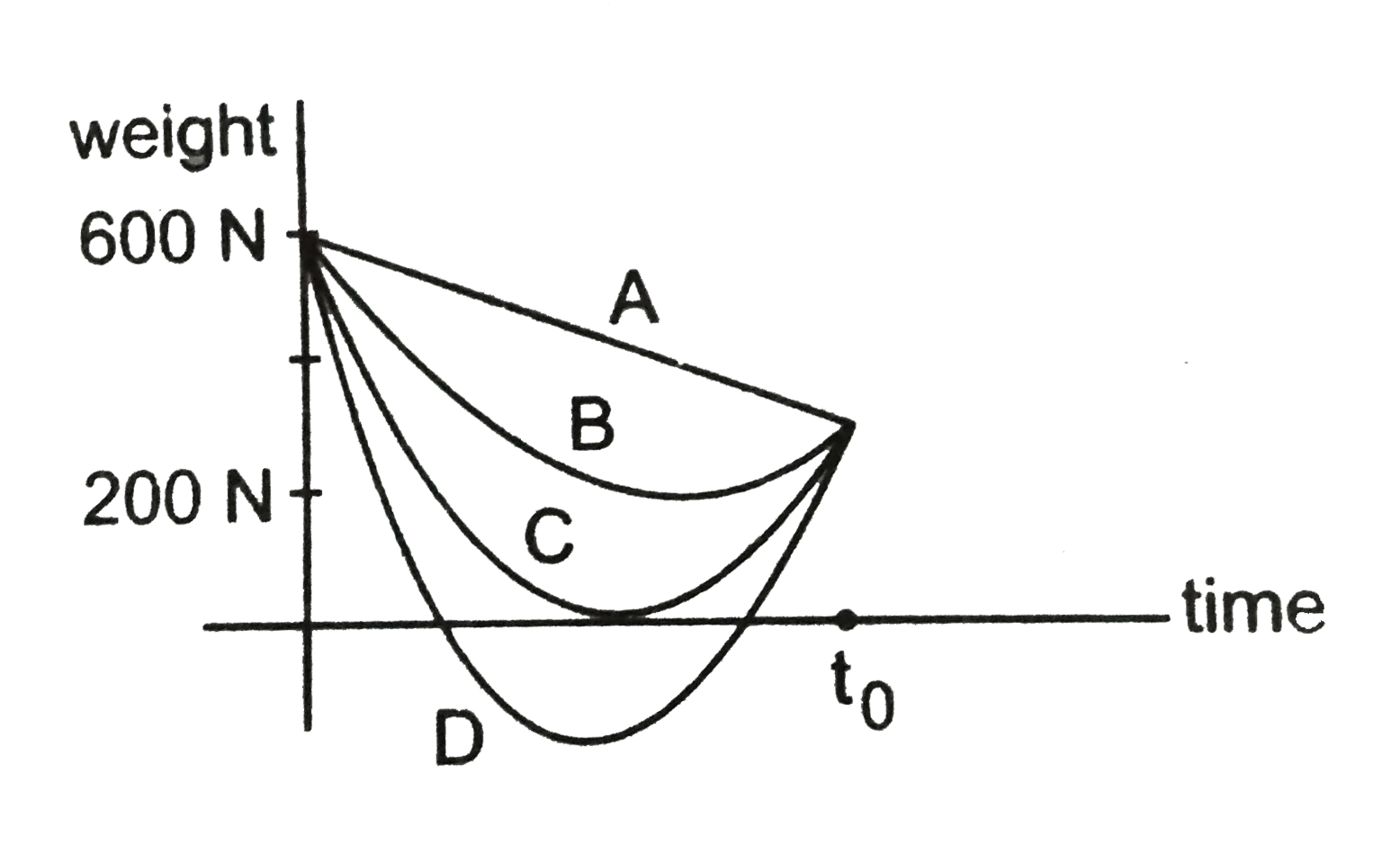View Solution