If the moment of inertion of a disc about an axis tangentially and parallel to its surface by I, then what will be the moment of inertia about the axis tangential but perpendicular to the surface
65I
34I
32I
54I
The correct Answer is:A
To solve the problem of finding the moment of inertia of a disc about an axis tangential but perpendicular to its surface, we can follow these steps:
Step 1: Understand the Given Information
We know that the moment of inertia of a disc about an axis tangentially and parallel to its surface is given as I.
Step 2: Use the Moment of Inertia Formula for a Disc
For a circular disc, the moment of inertia about an axis passing through its center and parallel to the surface is given by:
Icenter, parallel=14mr2
where m is the mass of the disc and r is its radius.
Step 3: Apply the Parallel Axis Theorem
To find the moment of inertia about the tangential axis parallel to the surface, we use the parallel axis theorem:
Itangential, parallel=Icenter, parallel+md2
where d is the distance from the center of the disc to the tangential axis. In this case, d=r (the radius of the disc).
Substituting the values, we have:
I=14mr2+mr2
I=14mr2+44mr2=54mr2
Step 4: Relate mr2 to I
From the above equation, we can express mr2:
mr2=45I
Step 5: Find the Moment of Inertia for the Perpendicular Axis
Now, we need to find the moment of inertia about the axis tangential but perpendicular to the surface. The moment of inertia about the center and perpendicular to the surface is given by:
Icenter, perpendicular=12mr2
Using the parallel axis theorem again:
Itangential, perpendicular=Icenter, perpendicular+md2
Here, d=r again, so:
I′=12mr2+mr2
I′=12mr2+22mr2=32mr2
Step 6: Substitute mr2 from Earlier
Now, substituting mr2=45I into the equation:
I′=32(45I)
I′=1210I=65I
Final Answer
Thus, the moment of inertia about the axis tangential but perpendicular to the surface is:
I′=65I
We know that the moment of inertia of a disc about an axis tangentially and parallel to its surface is given as I.
For a circular disc, the moment of inertia about an axis passing through its center and parallel to the surface is given by:
Icenter, parallel=14mr2
where m is the mass of the disc and r is its radius.
To find the moment of inertia about the tangential axis parallel to the surface, we use the parallel axis theorem:
Itangential, parallel=Icenter, parallel+md2
where d is the distance from the center of the disc to the tangential axis. In this case, d=r (the radius of the disc).
I=14mr2+mr2
I=14mr2+44mr2=54mr2
From the above equation, we can express mr2:
mr2=45I
Now, we need to find the moment of inertia about the axis tangential but perpendicular to the surface. The moment of inertia about the center and perpendicular to the surface is given by:
Icenter, perpendicular=12mr2
Itangential, perpendicular=Icenter, perpendicular+md2
Here, d=r again, so:
I′=12mr2+mr2
I′=12mr2+22mr2=32mr2
Now, substituting mr2=45I into the equation:
I′=32(45I)
I′=1210I=65I
Thus, the moment of inertia about the axis tangential but perpendicular to the surface is:
I′=65I
Topper's Solved these Questions
- BOOK - ICSECHAPTER - COMPETITION CARE UNITEXERCISE - GRAVITATION25videos
COMPETITION CARE UNIT
- BOOK - ICSECHAPTER - COMPETITION CARE UNITEXERCISE - PROPERTIES OF MATTER (ELASTICITY )22videos
COMPETITION CARE UNIT
- BOOK - ICSECHAPTER - COMPETITION CARE UNITEXERCISE - UNIFORM CIRCULAR MOTION25videos
COMPETITION CARE UNIT
- BOOK - ICSECHAPTER - CIRCULAR MOTION EXERCISE - MODULE 2 (FROM ROTATIONAL KINETIC ENERGY , WORK ,POWER)24videos
CIRCULAR MOTION
- BOOK - ICSECHAPTER - DIMENSIONSEXERCISE - SELECTED PROBLEMS (FROM CONVERSIONS OF ONE SYSTEMS OF UNITS INTO ANOTHER)9videos
DIMENSIONS
Similar Questions
Moment of inertia of a disc about an axis which is tangent and parallel to its plane is I . Then the moment of inertia of disc about a tangent, but perpendicular to its plane will be
View SolutionCalculate the moment of inertia of a disc about its any diameter ?
View SolutionCalculate the moment of inertia of a disc about its any diameter ?
View SolutionThe moment of inertia of a body about a given axis of rotation depends upon :-
View SolutionIf I1 is the moment of inertia of a thin rod about an axis perpendicular to its length and passing through its centre of mass and I2 is the moment of inertia of the ring about an axis perpendicular to plane of ring and passing through its centre formed by bending the rod, then
View SolutionCalculate the moment of inertia of the given rod about an axis CD.
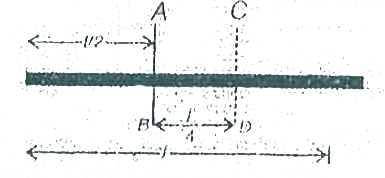 View Solution
View SolutionThe moment of inertia of ring about an axis passing through its diameter is I. Then moment of inertia of that ring about an axis passing through its centre and perpendicular to its plane is
View SolutionCalculate the moment of inertia of the given rod about an axis CD
 View Solution
View SolutionThe moment of inertia of a ring of mass M and radius R about PQ axis will be
 View Solution
View SolutionThe moment of inertia of a uniform ring about an axis passing through its centre and perpendicular to its plane is 100kgm2. What is the moment of inertia of the ring about its diameter ?
View Solution

