Two soap bubbles A and B have radii r1andr2 respectively. If r1<r2 than the excess pressure inside
bubbles A and B will be equal
bubbles A will be less than that in bubbles B
bubbles A will be greater than that in bubble B
bubbles A and B will be zero.
The correct Answer is:C
To solve the problem of comparing the excess pressure inside two soap bubbles A and B with radii r1 and r2 respectively, we can use the formula for the excess pressure inside a soap bubble. The excess pressure ΔP inside a soap bubble is given by the formula:
ΔP=4Tr
where T is the surface tension of the soap solution and r is the radius of the bubble.
1. Identify the Radii:
We have two soap bubbles, A and B, with radii r1 and r2 respectively. Given that r1<r2.
2. Apply the Excess Pressure Formula:
For bubble A, the excess pressure ΔP1 is:
ΔP1=4Tr1
For bubble B, the excess pressure ΔP2 is:
ΔP2=4Tr2
3. Compare the Excess Pressures:
Since r1<r2, we can analyze the relationship between ΔP1 and ΔP2:
- Since r1 is smaller than r2, 1r1>1r2.
- Therefore, ΔP1>ΔP2.
4. Conclusion:
The excess pressure inside bubble A (with radius r1) is greater than the excess pressure inside bubble B (with radius r2). Thus, we conclude:
ΔP1>ΔP2
Final Answer:
The correct option is that the excess pressure in bubble A will be greater than that in bubble B.
We have two soap bubbles, A and B, with radii r1 and r2 respectively. Given that r1<r2.
For bubble A, the excess pressure ΔP1 is:
ΔP1=4Tr1
For bubble B, the excess pressure ΔP2 is:
ΔP2=4Tr2
Since r1<r2, we can analyze the relationship between ΔP1 and ΔP2:
- Since r1 is smaller than r2, 1r1>1r2.
- Therefore, ΔP1>ΔP2.
The excess pressure inside bubble A (with radius r1) is greater than the excess pressure inside bubble B (with radius r2). Thus, we conclude:
ΔP1>ΔP2
The correct option is that the excess pressure in bubble A will be greater than that in bubble B.
Topper's Solved these Questions
- BOOK - ICSECHAPTER - COMPETITION CARE UNITEXERCISE - NDA EXAM QUESTIONS55videos
COMPETITION CARE UNIT
- BOOK - ICSECHAPTER - CIRCULAR MOTION EXERCISE - MODULE 2 (FROM ROTATIONAL KINETIC ENERGY , WORK ,POWER)24videos
CIRCULAR MOTION
- BOOK - ICSECHAPTER - DIMENSIONSEXERCISE - SELECTED PROBLEMS (FROM CONVERSIONS OF ONE SYSTEMS OF UNITS INTO ANOTHER)9videos
DIMENSIONS
Similar Questions
Two plane circular coilds P and Q have radii r1 and r2, respectively, (r1<<r2) and are coaxial as shown in fig. The number of turns in P and Q are respectively N1 and N2. If current in coil Q is varied steadily at a rate x ampere/second then the induced emf in the coil P will be approximatery -
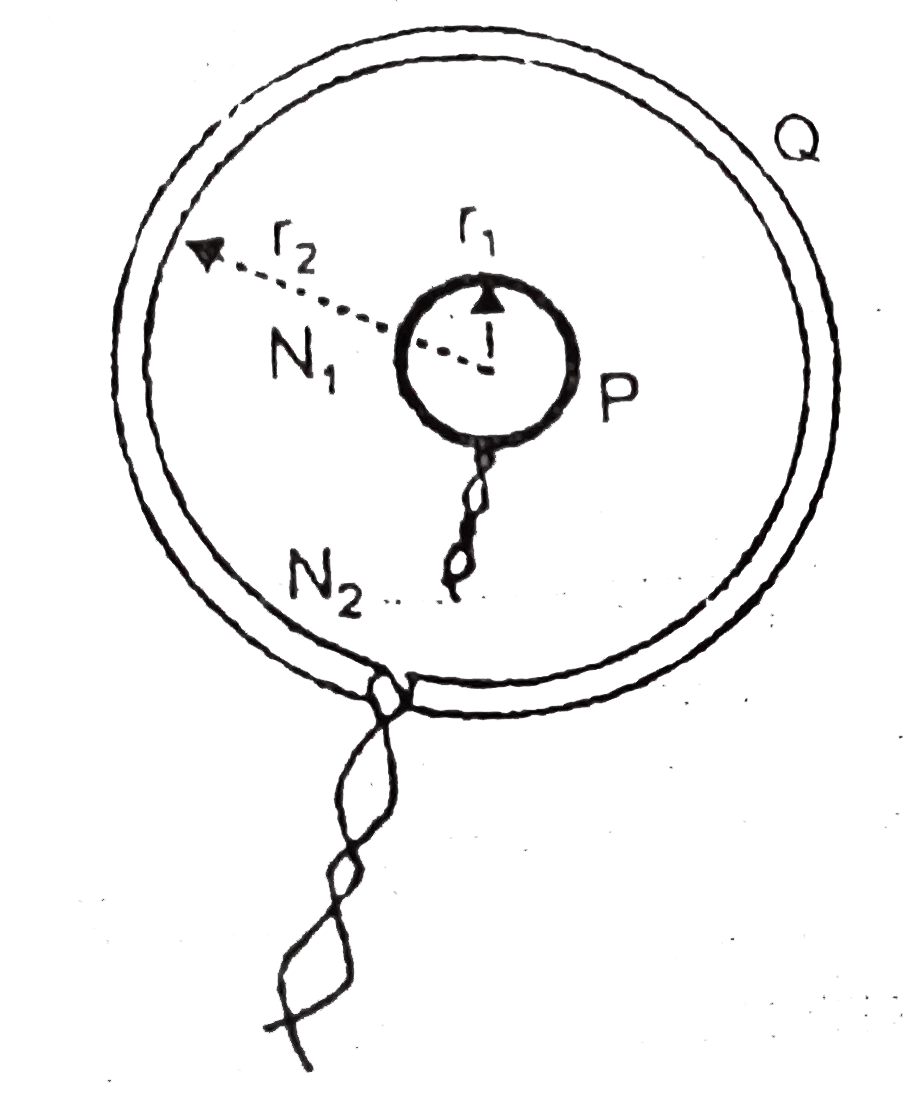 View Solution
View SolutionTwo soap bubbles are stuck together with an intermediate film separating them. Compute the radius of curvature of this film given that the radii of the bubbles in this arrangement are r1 and r2 respectively. If r1>r2 state clearly which way the intermediate film will bulge.
For the case when r1=r2=2cm calculate he radius of the bubble formed by bursting the intermediate film. The volume of a spherical dome of radius R and height h is πb2(3R−b)/3.View Solution
Knowledge Check
- Question 1 - Select One
Space between tow concentric spheres of radii r1andr2 such that r1<r2 is filled with a material of resistivity ρ. Find the resistance between inner and outer surface of the material
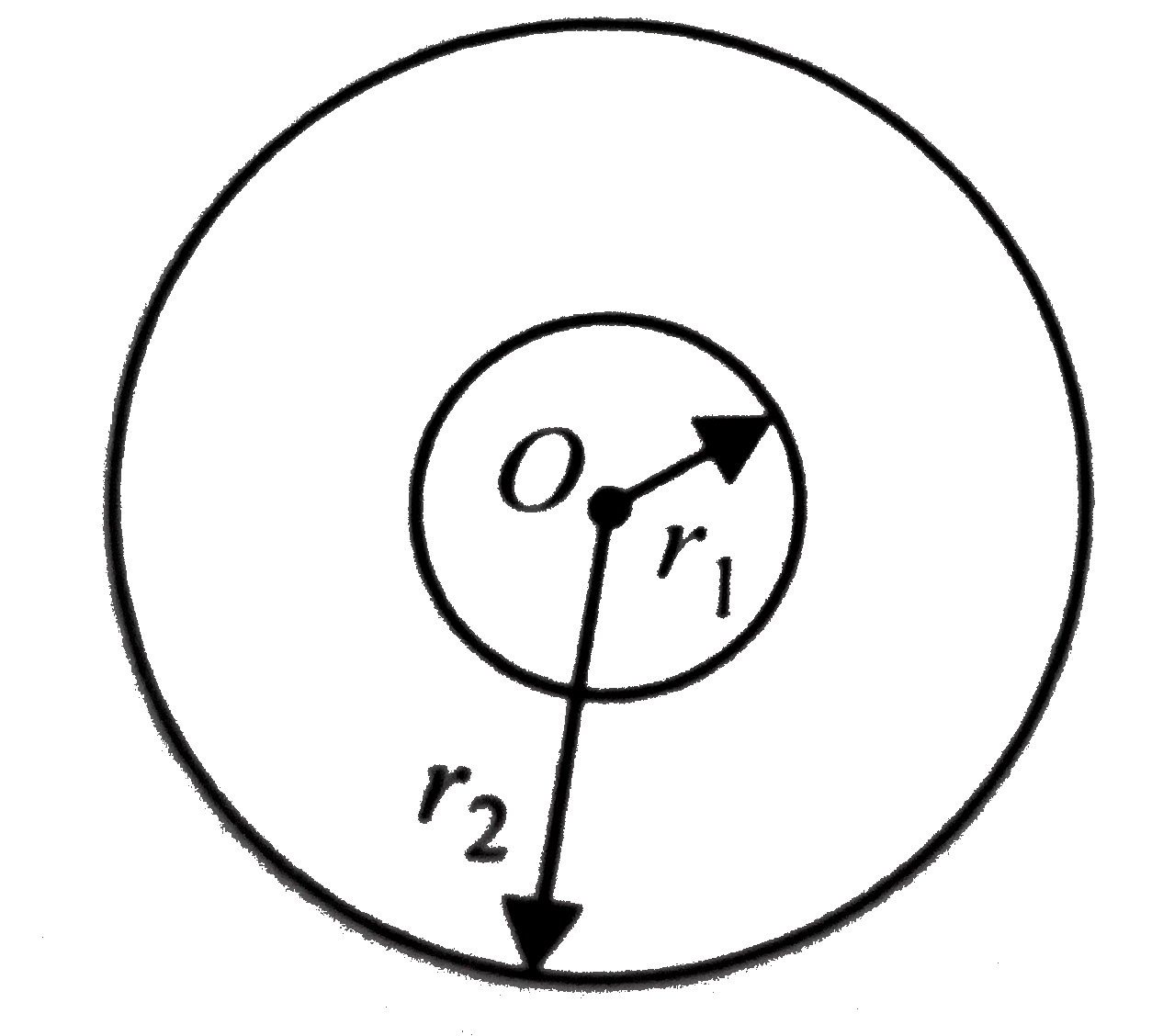 Ar1r2p2Br2−r1r1r2p4πCr1r2r2−r1p4πDnone of these.
Ar1r2p2Br2−r1r1r2p4πCr1r2r2−r1p4πDnone of these.
The circular orbit of two satellites have radii r1 and r2 respectively (r1<r2). If angular velosities of satellites are same, then their centripetal accelerations are related as
View SolutionUnder isothermal condition two soap bubbles of radii r1 and r2 coalesce to form a single bubble of radius r. The external pressure is p0. Find the surface tension of the soap in terms of the given parameters.
View SolutionTwo spherical nuclei have mass number 216 and 64 with their radii R1andR2 respectively. The ratio, R1R2 is equal to
View SolutionTwo circles centres AandB radii r1andr2 respectively. (i) touch each other internally iff |r1−r2|=AB. (ii) Intersect each other at two points iff |r1−r2|<AB<r1+r2. (iii) touch each other externally iff r1+r2=AB. (iv) are separated if AB>r1+r2. Number of common tangents to the two circles in case (i), (ii), (iii) and (iv) are 1, 2, 3 and 4 respectively. If circles (x−1)2+(y−3)2=r2andx2+y2−8x+2y+8=0 intersect each other at two different points, then : (A) 1<r<5 (B) 5<r<8 (C) 2<r<8 (D) none of these
View SolutionTwo cars of mass m1andm2 are moving in circle of radii r1andr2 , respectively . Their speeds are such that they make complete circles in the same time t . The ratio of their centripetal acceleration is :
View SolutionTwo cars of mass m1andm2 are moving in circle of radii r1andr2 , respectively . Their speeds are such that they make complete circles in the same time t . The ratio of their centripetal acceleration is :
View SolutionTwo metallic s pheres of radii R1 and R2 are connected b y a thin wire. If +q1~and+q_(2) are the charges on the two s pheres then
View Solution

