If x2+2x+72x+3<6, x∈ R then
x∈(−∞,−32)∪(11,∞)
x∈(−∞,−1)∪(11,∞)
x∈(−32,−1)
x∈(−∞,−32)∪(−1,11)
The correct Answer is:D
To solve the inequality x2+2x+72x+3<6, we will follow these steps:
Step 1: Rewrite the Inequality
We start by rewriting the inequality:
x2+2x+72x+3−6<0
This simplifies to:
x2+2x+7−6(2x+3)2x+3<0
Step 2: Simplify the Numerator
Now, we simplify the numerator:
x2+2x+7−12x−18=x2−10x−11
Thus, the inequality becomes:
x2−10x−112x+3<0
Step 3: Factor the Numerator
Next, we factor the quadratic expression in the numerator:
x2−10x−11=(x−11)(x+1)
So, we rewrite the inequality as:
(x−11)(x+1)2x+3<0
Step 4: Find Critical Points
We need to find the critical points where the expression is equal to zero or undefined:
1. x−11=0⇒x=11
2. x+1=0⇒x=−1
3. 2x+3=0⇒x=−32
The critical points are x=−1, x=11, and x=−32.
Step 5: Test Intervals
We will test the sign of the expression in the intervals defined by these critical points:
- Interval 1: (−∞,−32)
- Interval 2: (−32,−1)
- Interval 3: (−1,11)
- Interval 4: (11,∞)
Testing Interval 1: Choose x=−2
(−2−11)(−2+1)2(−2)+3=(−13)(−1)−1=13>0
Testing Interval 2: Choose x=−1.5
(−1.5−11)(−1.5+1)2(−1.5)+3=(−12.5)(−0.5)0 (undefined)
Testing Interval 3: Choose x=0
(0−11)(0+1)2(0)+3=(−11)(1)3=−113<0
Testing Interval 4: Choose x=12
(12−11)(12+1)2(12)+3=(1)(13)27>0
Step 6: Determine the Solution
From our tests, we find:
- The expression is positive in (−∞,−32) and (11,∞).
- The expression is negative in (−1,11).
Thus, the solution to the inequality (x−11)(x+1)2x+3<0 is:
x∈(−32,−1)∪(−1,11)
Final Answer
The solution set is:
x∈(−∞,−32)∪(−1,11)
---
We start by rewriting the inequality:
x2+2x+72x+3−6<0
This simplifies to:
x2+2x+7−6(2x+3)2x+3<0
Now, we simplify the numerator:
x2+2x+7−12x−18=x2−10x−11
Thus, the inequality becomes:
x2−10x−112x+3<0
Next, we factor the quadratic expression in the numerator:
x2−10x−11=(x−11)(x+1)
So, we rewrite the inequality as:
(x−11)(x+1)2x+3<0
We need to find the critical points where the expression is equal to zero or undefined:
1. x−11=0⇒x=11
2. x+1=0⇒x=−1
3. 2x+3=0⇒x=−32
We will test the sign of the expression in the intervals defined by these critical points:
- Interval 1: (−∞,−32)
- Interval 2: (−32,−1)
- Interval 3: (−1,11)
- Interval 4: (11,∞)
(−2−11)(−2+1)2(−2)+3=(−13)(−1)−1=13>0
(−1.5−11)(−1.5+1)2(−1.5)+3=(−12.5)(−0.5)0 (undefined)
(0−11)(0+1)2(0)+3=(−11)(1)3=−113<0
(12−11)(12+1)2(12)+3=(1)(13)27>0
From our tests, we find:
- The expression is positive in (−∞,−32) and (11,∞).
- The expression is negative in (−1,11).
x∈(−32,−1)∪(−1,11)
The solution set is:
x∈(−∞,−32)∪(−1,11)
Topper's Solved these Questions
- QUADRATIC EQUATIONS BOOK - VIKAS GUPTA (BLACK BOOK) ENGLISHCHAPTER - QUADRATIC EQUATIONS EXERCISE - EXERCISE (ONE OR MORE THAN ONE ANSWER IS/ARE CORRECT)
42 Videos
- QUADRATIC EQUATIONS BOOK - VIKAS GUPTA (BLACK BOOK) ENGLISHCHAPTER - QUADRATIC EQUATIONS EXERCISE - EXERCISE (COMPREHENSION TYPE PROBLEMS)
23 Videos
- PROBABILITY BOOK - VIKAS GUPTA (BLACK BOOK) ENGLISHCHAPTER - PROBABILITY EXERCISE - Exercise -5 : Subjective Type problems
11 Videos
- SEQUENCE AND SERIES BOOK - VIKAS GUPTA (BLACK BOOK) ENGLISHCHAPTER - SEQUENCE AND SERIES EXERCISE - EXERCISE (SUBJECTIVE TYPE PROBLEMS)
21 Videos
Similar Questions
Knowledge Check
The solution set of 2x+13<3x−25x∈R on the number line is
A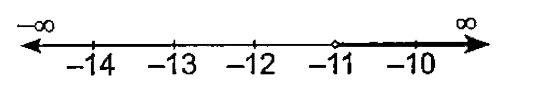 B
B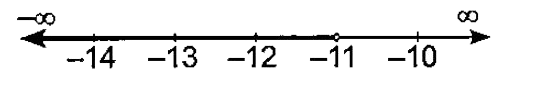 C
C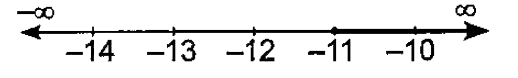 D
D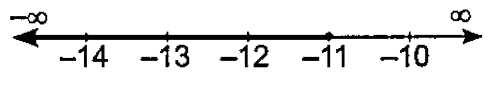
If x4<5x−23−7x−35,x∈R then
Ax∈(−∞,4]Bx∈(−∞,4)Cx∈(4,∞)Dx∈[4,∞)If 2x−3<x+1<4x+7,x∈R then the solution set of x on the number line is:
A B
B C
C D
D
Number of intergral value of x satisfying the inequality x2+6x−7|x+4|<0 is :
View SolutionSolve the following inequation and represent the solution set on the number line.
−3<−12−2x3≤56,x∈R.
View SolutionIf 9x+1+(a2−4a−2)3x+1<0for allx∈R, then
View SolutionIf −5<2x−3≤x+2,x∈R, then the solution set of x on the number line is
View SolutionThe solution set of 6≤−3(2x−4)<12,x∈R is
View Solution
