Graph of f(x)=x & g(x)=2+lnx , x>0 where e is base of natural log. Graph intersect at=?
once in (0,1) and never in (1,∞)
once in (0,1) and once in (e2,∞)
once in (0,1) and one in (e,e2)
more than twice in (0,∞)
The correct Answer is:C
To find the points of intersection of the graphs of the functions f(x)=x and g(x)=2+lnx for x>0, we need to set the two functions equal to each other:
f(x)=g(x)
This gives us the equation:
x=2+lnx
Step 1: Rearranging the Equation
We can rearrange this equation to isolate the logarithmic term:
x−2=lnx
Step 2: Analyzing the Functions
To analyze the intersection points, we can define a new function:
h(x)=x−2−lnx
We want to find the values of x for which h(x)=0.
Step 3: Finding the Derivative
Next, we can find the derivative of h(x) to understand its behavior:
h′(x)=1−1x
Step 4: Critical Points
Setting the derivative to zero to find critical points:
1−1x=0⟹x=1
Step 5: Analyzing the Sign of the Derivative
- For x<1, h′(x)<0 (decreasing).
- For x>1, h′(x)>0 (increasing).
This indicates that h(x) has a minimum at x=1.
Step 6: Evaluating h(1)
Now, we evaluate h(1):
h(1)=1−2−ln(1)=1−2−0=−1
Step 7: Evaluating h(2)
Next, we evaluate h(2):
h(2)=2−2−ln(2)=0−ln(2)=−ln(2)<0
Step 8: Evaluating h(e)
Now, we evaluate h(e):
h(e)=e−2−ln(e)=e−2−1=e−3
Since e≈2.718, we find that h(e)>0.
Step 9: Conclusion on Intersections
Since h(1)<0 and h(e)>0, by the Intermediate Value Theorem, there is at least one root in the interval (1,e).
Step 10: Finding the Second Intersection
To find the second intersection, we can evaluate h(x) at x=e2:
h(e2)=e2−2−ln(e2)=e2−2−2=e2−4
Since e2≈7.389, we find that h(e2)>0. Therefore, there is a root in the interval (e,e2).
Final Result
Thus, the graphs of f(x) and g(x) intersect at two points: one in the interval (1,e) and another in the interval (e,e2).
We can rearrange this equation to isolate the logarithmic term:
To analyze the intersection points, we can define a new function:
Next, we can find the derivative of h(x) to understand its behavior:
Setting the derivative to zero to find critical points:
- For x<1, h′(x)<0 (decreasing).
- For x>1, h′(x)>0 (increasing).
Now, we evaluate h(1):
Next, we evaluate h(2):
Now, we evaluate h(e):
Since h(1)<0 and h(e)>0, by the Intermediate Value Theorem, there is at least one root in the interval (1,e).
To find the second intersection, we can evaluate h(x) at x=e2:
Thus, the graphs of f(x) and g(x) intersect at two points: one in the interval (1,e) and another in the interval (e,e2).
Topper's Solved these Questions
- QUADRATIC EQUATIONS BOOK - VK JAISWAL ENGLISHCHAPTER - QUADRATIC EQUATIONS EXERCISE - EXERCISE (ONE OR MORE THAN ONE ANSWER IS/ARE CORRECT)
42 Videos
- QUADRATIC EQUATIONS BOOK - VK JAISWAL ENGLISHCHAPTER - QUADRATIC EQUATIONS EXERCISE - EXERCISE (COMPREHENSION TYPE PROBLEMS)
23 Videos
- PROBABILITY BOOK - VK JAISWAL ENGLISHCHAPTER - PROBABILITY EXERCISE - Exercise -5 : Subjective Type problems
11 Videos
- SEQUENCE AND SERIES BOOK - VK JAISWAL ENGLISHCHAPTER - SEQUENCE AND SERIES EXERCISE - EXERCISE (SUBJECTIVE TYPE PROBLEMS)
21 Videos
Similar Questions
Knowledge Check
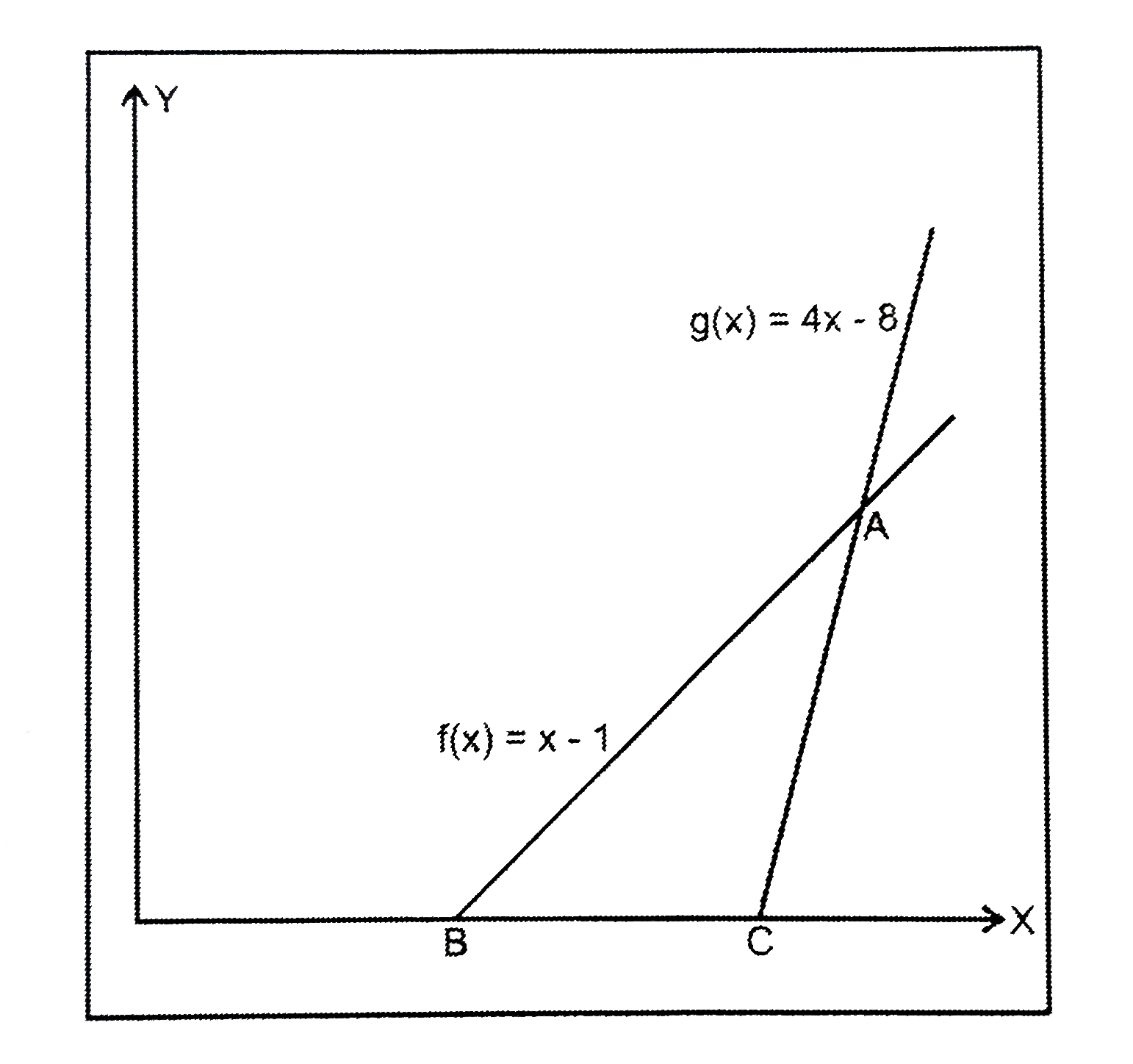
What is the area of the triangle ABC bounded by the graphs of f(x) = x - 1 and g(X) = 4x - 8 and the X -axis as shown in the graph below ?A23B1C43D2The function f is defined by f(x)=x4−4x4−x2+cx−12 , where c is a constant.In the xy-plane, the graph of f intersects the x-axis in the four points (-2,0), (1,0), (p,0), and (q,0). What is the value of c ?
A16B−16CpqDqpIf f(x)=ex+2x, then f(ln2)=
A1.20B2.69C2.77D3.39
Draw the graph of f(x)=esinx.
View SolutionDraw the graph of f(x)=sgn(logex).
View SolutionFind fog and gof if:
f(x)=ex,g(x)=lnx
View SolutionA line x=k intersects the graph of y=log4x and y=log4(x+4). The distance between the points of intersection is 0.5, then the value of k is
View SolutionIf f(x)=logx(lnx) then f'(x) at x=e is
View Solution
