B1,B2, and B3, are three balloos ascending with velocities v, 2v, and 3v, respectively, If a bomb is dropped from each when they are at the same height, then.
Bomb from B1 reaches ground first
Bomb from B2 reaches ground first
Bomb from B3 reaches ground first
They reach the ground simultaneously
The correct Answer is:A
To solve the problem, we need to analyze the motion of the bombs dropped from the three balloons, B1, B2, and B3, which are ascending with velocities v, 2v, and 3v respectively.
1. Understanding the Initial Conditions:
- The balloons are at the same height when the bombs are dropped.
- The velocities of the balloons are:
- Balloon B1: v1=v
- Balloon B2: v2=2v
- Balloon B3: v3=3v
2. Analyzing the Motion of the Bombs:
- When a bomb is dropped from a balloon, it initially has the same upward velocity as the balloon.
- The bombs will experience the acceleration due to gravity (g) acting downwards.
3. Finding the Maximum Height:
- Each bomb will first ascend to a maximum height before descending.
- The time taken to reach the maximum height can be calculated using the formula:
t=ug
- Where u is the initial velocity of the bomb (which is the same as the velocity of the balloon at the moment of release).
4. Calculating the Maximum Height for Each Bomb:
- For bomb from B1 (initial velocity = v):
h1=v22g
- For bomb from B2 (initial velocity = 2v):
h2=(2v)22g=4v22g=2v2g
- For bomb from B3 (initial velocity = 3v):
h3=(3v)22g=9v22g
5. Total Distance Fallen by Each Bomb:
- After reaching the maximum height, each bomb will fall to the ground. The total distance fallen for each bomb is the sum of the height it ascends and the distance it falls back to the ground.
- The time taken to fall from height h to the ground can be calculated using:
t=√2hg
6. Calculating Total Time for Each Bomb:
- For bomb from B1:
t1=vg+√2h1g=vg+
⎷2⋅v22gg=vg+√v2g2=vg+vg=2vg
- For bomb from B2:
t2=2vg+√2h2g=2vg+
⎷2⋅2v2gg=2vg+√4v2g2=2vg+2vg=4vg
- For bomb from B3:
t3=3vg+√2h3g=3vg+
⎷2⋅9v22gg=3vg+√9v2g2=3vg+3vg=6vg
7. Comparing Times:
- From the calculations:
- t1=2vg
- t2=4vg
- t3=6vg
- The bomb from B1 reaches the ground first because it takes the least time.
Conclusion:
The bomb from balloon B1 reaches the ground first.
- The balloons are at the same height when the bombs are dropped.
- The velocities of the balloons are:
- Balloon B1: v1=v
- Balloon B2: v2=2v
- Balloon B3: v3=3v
- When a bomb is dropped from a balloon, it initially has the same upward velocity as the balloon.
- The bombs will experience the acceleration due to gravity (g) acting downwards.
- Each bomb will first ascend to a maximum height before descending.
- The time taken to reach the maximum height can be calculated using the formula:
t=ug
- Where u is the initial velocity of the bomb (which is the same as the velocity of the balloon at the moment of release).
- For bomb from B1 (initial velocity = v):
h1=v22g
- For bomb from B2 (initial velocity = 2v):
h2=(2v)22g=4v22g=2v2g
- For bomb from B3 (initial velocity = 3v):
h3=(3v)22g=9v22g
- After reaching the maximum height, each bomb will fall to the ground. The total distance fallen for each bomb is the sum of the height it ascends and the distance it falls back to the ground.
- The time taken to fall from height h to the ground can be calculated using:
t=√2hg
- For bomb from B1:
t1=vg+√2h1g=vg+
⎷2⋅v22gg=vg+√v2g2=vg+vg=2vg
- For bomb from B2:
t2=2vg+√2h2g=2vg+
⎷2⋅2v2gg=2vg+√4v2g2=2vg+2vg=4vg
- For bomb from B3:
t3=3vg+√2h3g=3vg+
⎷2⋅9v22gg=3vg+√9v2g2=3vg+3vg=6vg
- From the calculations:
- t1=2vg
- t2=4vg
- t3=6vg
- The bomb from B1 reaches the ground first because it takes the least time.
The bomb from balloon B1 reaches the ground first.
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-1EXERCISE - Graphical Concept17videos
KINEMATICS-1
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-1EXERCISE - Graphical cancept1videos
KINEMATICS-1
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-1EXERCISE - Subjective29videos
KINEMATICS-1
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GRAVITATIONEXERCISE - INTEGER_TYPE1videos
GRAVITATION
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-2EXERCISE - Exercise Integer9videos
KINEMATICS-2
Similar Questions
P, Q and R are three balloons ascending with velocities U, 4U and 8U respectively. If stones of the same mass be dropped from each, when they are at the same height, then
View SolutionTwo bodies A and B of same mass are moving with velocities v and 2v, respectively. Compare their inertia
View SolutionTwo bodies A and B of same mass are moving with velocities v and 2v, respectively. Compare their momentum.
View SolutionTwo balls A and B of masses m and 2 m are in motion with velocities 2v and v, respectively. Compare: Their inertia.
View SolutionTwo balls A and B of masses m and 2 m are in motion with velocities 2v and v, respectively. Compare: The force needed to stop them in the same
View SolutionTwo balls A and B of masses m and 2 m are in motion with velocities 2v and v, respectively. Compare: Their momentum.
View SolutionTwo projectiles A and B are thrown from the same point with velocities v and v2 respectively. If B is thrown at an angle 45∘ with horizontal.What is the inclination of A.when their ranges are the same?
View SolutionIn the figure shown B1,B2 and B3 are three bulbs rated as (200V, 50 W), (200V, 100W) and (200V, 25W) respectively. Find the current through each bulb and which bulb will give more light ?
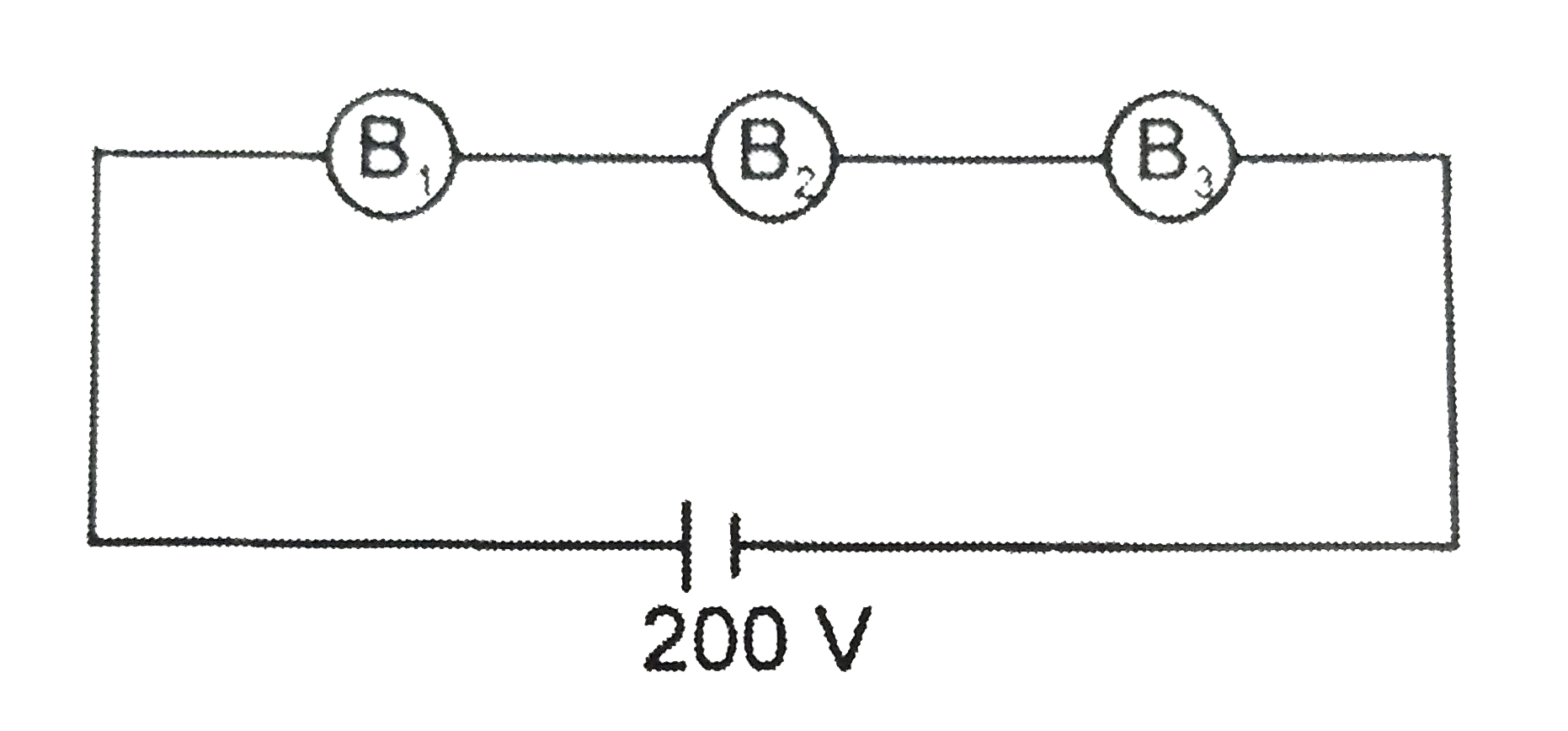 View Solution
View SolutionTwo identical particles move towards each other with velocity 2v and v, respectively. The velocity of the centre of mass is:
View SolutionTwo objects A and B are moving in opposite directions with velocities vAandvB respectively, the magnitude of relative velocity of A w.r.t. B is
View Solution

