A block of mass m moving on a fixed smooth hemisphere of rudius R. If speed of block at top most point of the hemisohere is √gR as shown in the figure, then the angle (θ) with the vertical, where the normal contact force becomes zero will be
cos−1(23
cos−1(13)
cos−1(12)
Zero
Step by step video & image solution for A block of mass m moving on a fixed smooth hemisphere of rudius R. If speed of block at top most point of the hemisohere is sqrtgR as shown in the figure, then the angle (theta) with the vertical, where the normal contact force becomes zero will be by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
A small block of mass m has speed√gR2 at the top most point of a fixed hemisphere of radius R as shown in figure. The angle θ, when block loses the contact with the hemisphere is
_PHY_E05_149_Q01.png)
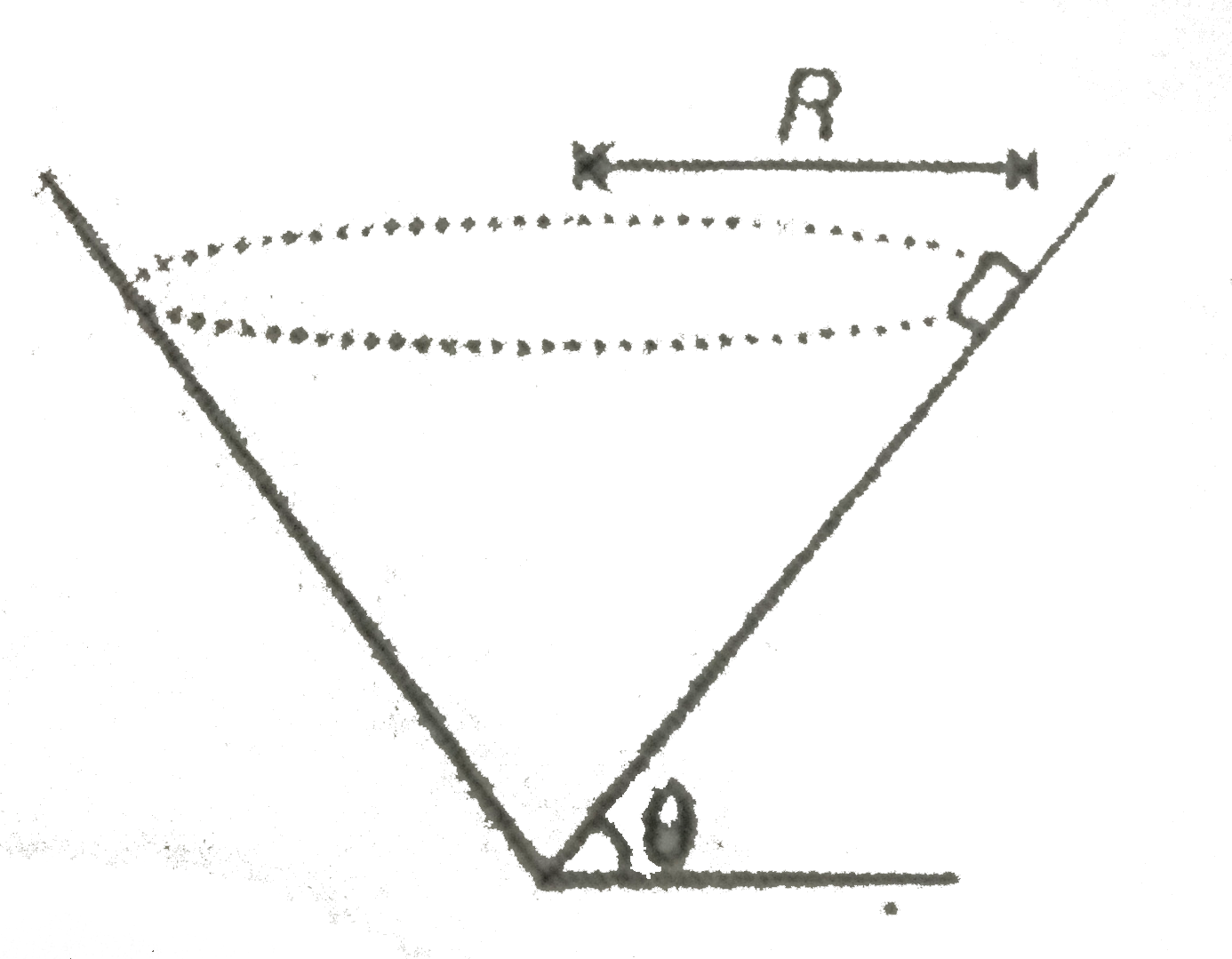
View SolutionA block of mass m is moving in a circle of radius R with speed v inside a smooth cone as shown in figure. Choose the wrong options
View SolutionA smooth hemisphere of mass M is kept on a smooth surface. A block of mass m(=M/3) is kept on the top of the hemisphere as shown in the figure. The hemisphere is displaced slightly ang both the hemisphere and the block starts moving. At an angle θ with the vertical ( subtended by the block at the centre of the hemisphere ) , the relation between the velocity of the block ( V) and the velocity of the hemishere ( v0 ) is (V is the velocity of the block w.r.t. the hemisphere at that instant . )

View SolutionA particle of mass m is placed in equilibrium at the top of a fixed rough hemisphere of radius R. Now the particle leaves the contact with the surface of the hemisphere at angular position θ with the vertical where cosθ=35. if the work done against friction is 2mgR10x, find x.
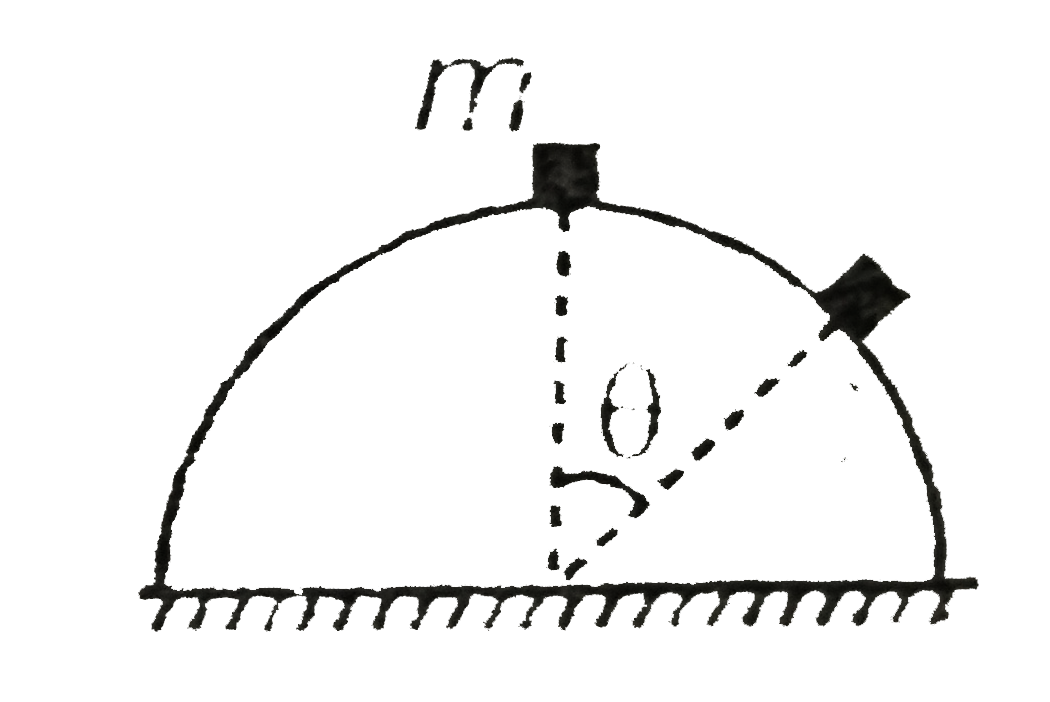
View SolutionA small block of mass m is released from rest from position A inside a smooth hemispherical bowl of radius R as shown in figure Choose the wrong option.

View SolutionA small block of mass m is pushed on a smooth track from position A with a velocity 2√5 times the minimum velocity required to reach point D. The block will leave the contact with track at the point where normal force between them becomes zero.
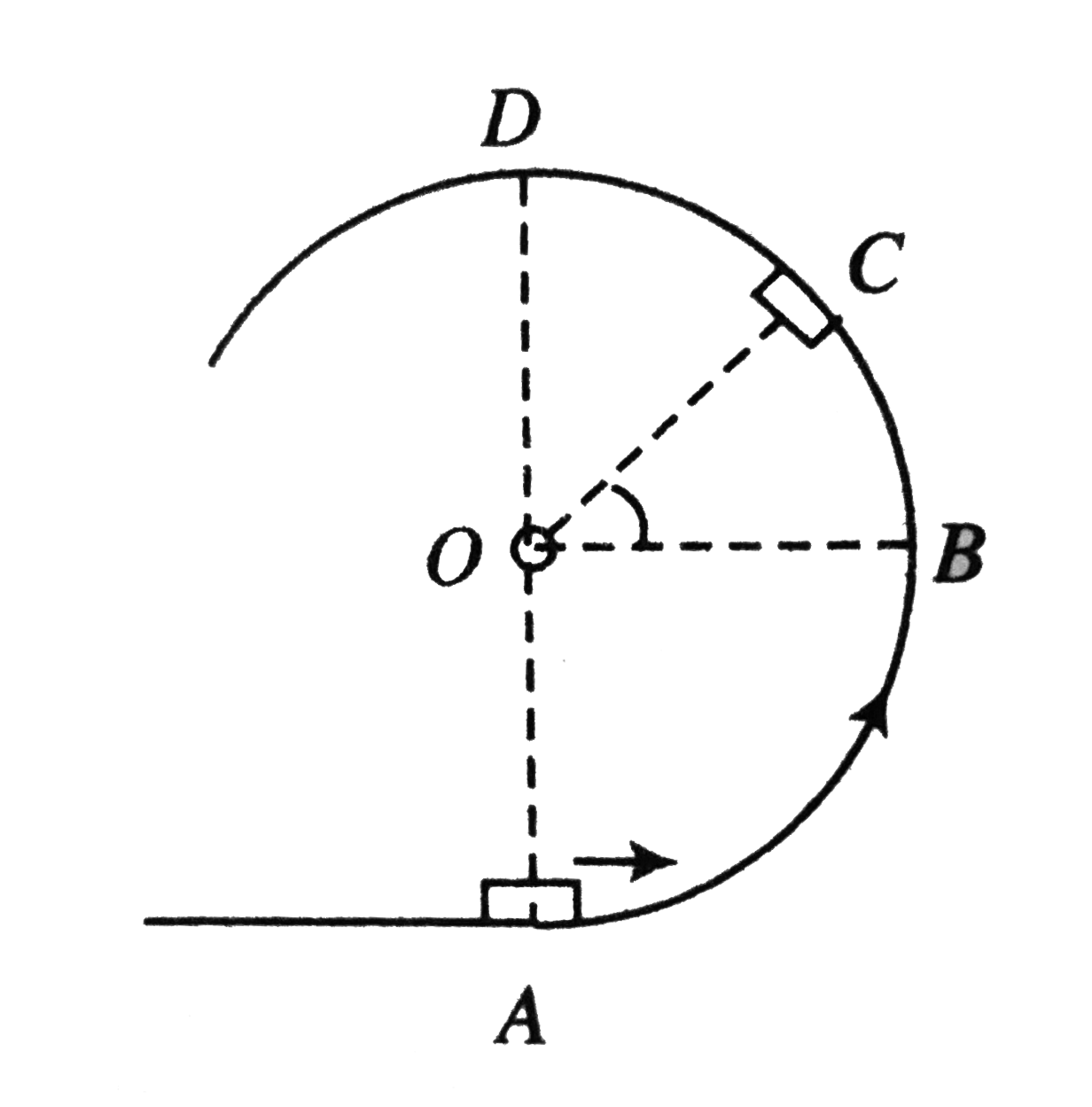
Find where the maximum contact force occurs between the block and the track.
View SolutionA small block of mass m is placed at rest on the top of a smooth wedge of mass M, which in turn is placed at rest on a smooth horizontal surface as shown in figure. If h be the height of wedge and θ is the inclination, then the distance moved by the wedge as the block reaches the foot of the wedge is
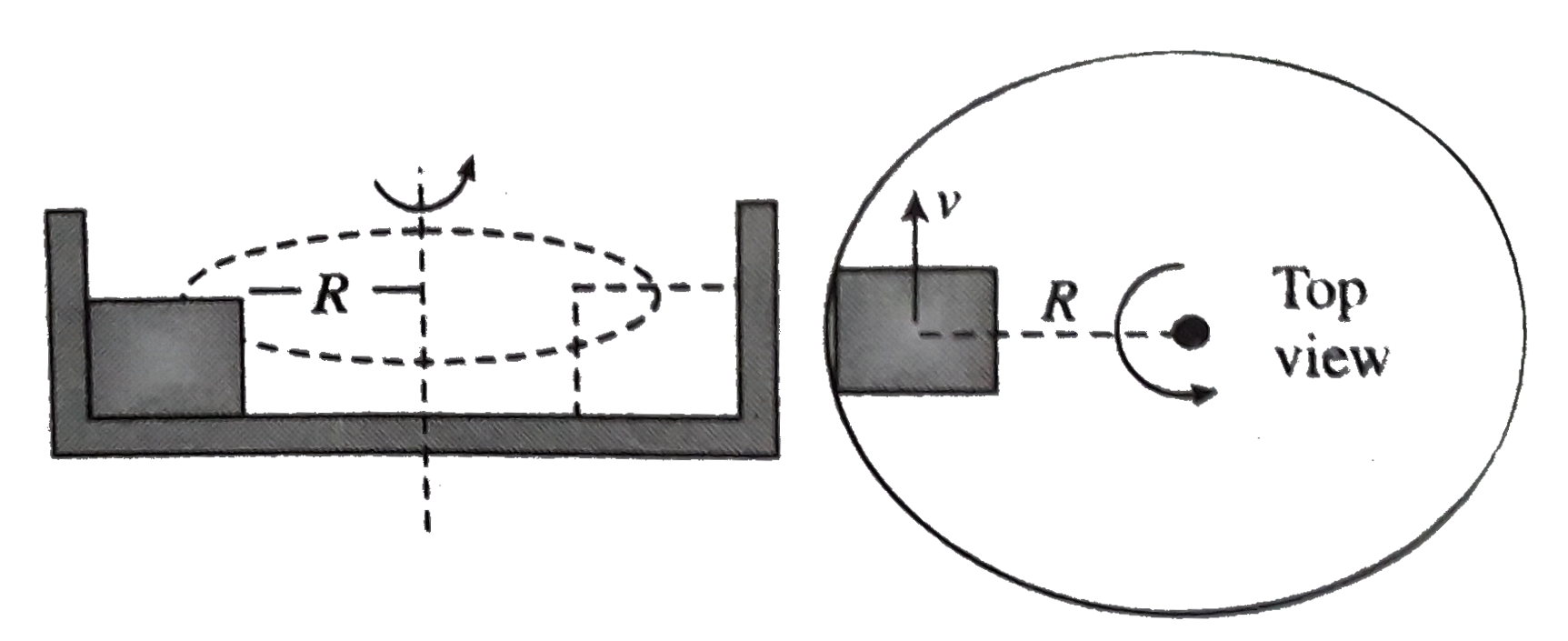
View SolutionA block of mass m is revolving in a smooth horizontal plane with a constant speed v.If the radius of the circle path is R find the total contact force received by the block
View SolutionA horizontal force F is applied to a block of mass m on a smooth fixed inclined plane of inclination θ to the horizontal as shown in the figure. Resultant force on the block up the plane is:

View SolutionA block of mass m, lying on a smooth horizontal surface, is attached to a spring (of negligible mass) of spring constant k. The other end of the spring is fixed, as shown in the figure. The block is initally at rest in its equilibrium position. If now the block is pulled withe a constant force F, the maximum speed of the block is :

View Solution
