A train is moving at a constant speed V when its driverobserves another train in front of him on the same track and voing in the same direction with constant speed v. If the distance berween the trains is x. Trains is x then what should be the minimum retardation of the train so as to avoed collision?.
(V+v)2x
(V+v)2x
c. (V+v)22x
(V+v)22x
The correct Answer is:D
To solve the problem of determining the minimum retardation required for the first train to avoid a collision with the second train, we can follow these steps:
1. Identify the Variables:
- Let the speed of the first train be V.
- Let the speed of the second train be v.
- Let the distance between the two trains be x.
2. Relative Motion Concept:
- Since both trains are moving in the same direction, we can analyze the situation using relative motion.
- The relative speed of the first train with respect to the second train is given by:
urelative=V−v
3. Final Relative Velocity:
- To avoid collision, the final relative velocity when the first train comes to a stop should be zero:
vrelative, final=0
4. Using the Equation of Motion:
- We can use the third equation of motion, which states:
v2=u2+2as
- In our case, substituting for the relative motion:
02=(V−v)2+2(−a)x
- Here, a is the retardation (deceleration), and s is the distance x.
5. Rearranging the Equation:
- Rearranging the equation gives:
0=(V−v)2−2ax
- This can be rewritten as:
2ax=(V−v)2
6. Solving for Retardation:
- Now, solving for a (retardation):
a=(V−v)22x
Final Answer:
The minimum retardation required for the first train to avoid a collision with the second train is given by:
a=(V−v)22x
- Let the speed of the first train be V.
- Let the speed of the second train be v.
- Let the distance between the two trains be x.
- Since both trains are moving in the same direction, we can analyze the situation using relative motion.
- The relative speed of the first train with respect to the second train is given by:
urelative=V−v
- To avoid collision, the final relative velocity when the first train comes to a stop should be zero:
vrelative, final=0
- We can use the third equation of motion, which states:
v2=u2+2as
- In our case, substituting for the relative motion:
02=(V−v)2+2(−a)x
- Here, a is the retardation (deceleration), and s is the distance x.
- Rearranging the equation gives:
0=(V−v)2−2ax
- This can be rewritten as:
2ax=(V−v)2
- Now, solving for a (retardation):
a=(V−v)22x
The minimum retardation required for the first train to avoid a collision with the second train is given by:
a=(V−v)22x
Topper's Solved these Questions
- KINEMATICS-1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-1EXERCISE - Graphical Concept
17 Videos
- KINEMATICS-1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-1EXERCISE - Graphical cancept
1 Videos
- KINEMATICS-1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-1EXERCISE - Subjective
29 Videos
- GRAVITATIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GRAVITATIONEXERCISE - INTEGER_TYPE
1 Videos
- KINEMATICS-2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-2EXERCISE - Exercise Integer
9 Videos
Similar Questions
The driver of a train moving at 72kmh−1 sights another train moving at 4ms−1 on the same track and in the same direction. He instantly applies brakes to produces a retardation of 1ms−2. The minimum distance between the trains so that no collision occurs is
View SolutionAn express train is moving with a velocity v1. Its driver finds another train is movig on the same track in the same direction with velocity v2. To escape collision, driver applies a retardation a on the train. The minimum time of escaping collision be
View Solution
Knowledge Check
Train X is traveling at a constant speed of 30 miles per hour and Train Y is traveling at a constant speed of 40 miles per hour. If the two trains are travelling in the same direction along the same route but Train X is 25 miles ahead of Train Y how many hours will it be until Train Y iis 10 miles ahead of Train X?
A1.5B2.0C2.5D3.5
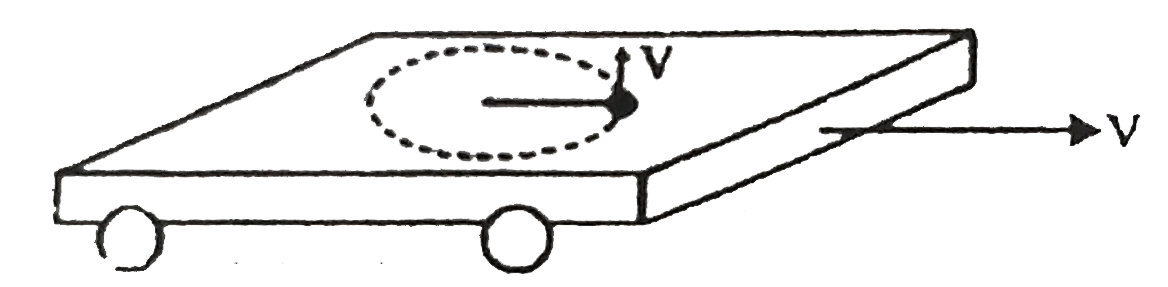
On a train moving along east with a constant speed v, a boy revolves a bob with string of length l on smooth surface of a train, with equal constant speed v relative to train. Mark the correct option(s).
View SolutionTwo train are moving in a straight line in the same direction with a speed of 80 km/h. The relative velocity of one trains w.r.t. each other is
View SolutionA train is moving with a constant speed along a circular track. The engine of the train emits a sound of frequency f. The frequency heard by the guard at the rear end of the train.
View SolutionA train of mass M is moving on a circular track of radius R with constant speed v. The length of the train is half of the perimeter of the track. The linear momentum of the train will be
View SolutionA train of mass M is moving on a circular track of radius R with constant speed v. The length of the train is half of the perimeter of the track. The linear momentum of the train will be
View SolutionTwo trains going in opposite directions with the same speed are at rest relative to each other. True/False.
View SolutionA train is running at a constant speed of 90 km/h on a straight track. A person standing at the top of a boggey moves in the direction of motion of the train such that he covers 1 meters on the train each second. The speed of the person with respect to ground to -
View Solution
