Two train are moving in a straight line in the same direction with a speed of 80 km/h. The relative velocity of one trains w.r.t. each other is
80 km/h
40 km/h
Zero
160 km/h
The correct Answer is:C
To solve the problem of finding the relative velocity of one train with respect to the other when both trains are moving in the same direction at the same speed, we can follow these steps:
1. Identify the velocities of the trains:
- Let the speed of Train A (VA) = 80 km/h.
- Let the speed of Train B (VB) = 80 km/h.
2. Understand the concept of relative velocity:
- The relative velocity of one object with respect to another is given by the formula:
VAB=VA−VB
- Here, VAB is the velocity of Train A with respect to Train B.
3. Substitute the values into the formula:
- Using the values we identified:
VAB=80 km/h−80 km/h
4. Calculate the relative velocity:
- Performing the subtraction:
VAB=0 km/h
5. Interpret the result:
- A relative velocity of 0 km/h indicates that from the perspective of either train, the other train appears to be at rest. This means that both trains are moving together at the same speed in the same direction.
Conclusion:
The relative velocity of one train with respect to the other is 0 km/h.
- Let the speed of Train A (VA) = 80 km/h.
- Let the speed of Train B (VB) = 80 km/h.
- The relative velocity of one object with respect to another is given by the formula:
VAB=VA−VB
- Here, VAB is the velocity of Train A with respect to Train B.
- Using the values we identified:
VAB=80 km/h−80 km/h
- Performing the subtraction:
VAB=0 km/h
- A relative velocity of 0 km/h indicates that from the perspective of either train, the other train appears to be at rest. This means that both trains are moving together at the same speed in the same direction.
The relative velocity of one train with respect to the other is 0 km/h.
Topper's Solved these Questions
- MOTION IN STRAIGHT LINEBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOTION IN STRAIGHT LINEEXERCISE - Assignment (SECTION - B)
19 Videos
- MOTION IN STRAIGHT LINEBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOTION IN STRAIGHT LINEEXERCISE - Assignment (SECTION - C)
7 Videos
- MOTION IN STRAIGHT LINEBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOTION IN STRAIGHT LINEEXERCISE - Try Yourself
40 Videos
- MOTION IN A STRAIGHT LINEBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - ASSIGNMENT (SECTION - D)
15 Videos
- MOVING CHARGE AND MAGNESIUMBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOVING CHARGE AND MAGNESIUMEXERCISE - SECTION D
16 Videos
Similar Questions
Two cars are moving is one a same line dimension in opposite direction with the same speed v. The relative velocity of two cars w.r.t. each other is
View SolutionBuses A and B are moving in the same direction with speed 20ms−1 and 15ms−1 respectively. Find the relative velcoity of A w.r.t. B and relative velocity of B w.r.t. A.
View SolutionShown in the figure are the velocity time graphs of the two particle P1 and P2 moving in same straight line in same direction. Which of the following statements about their relative motion is true?
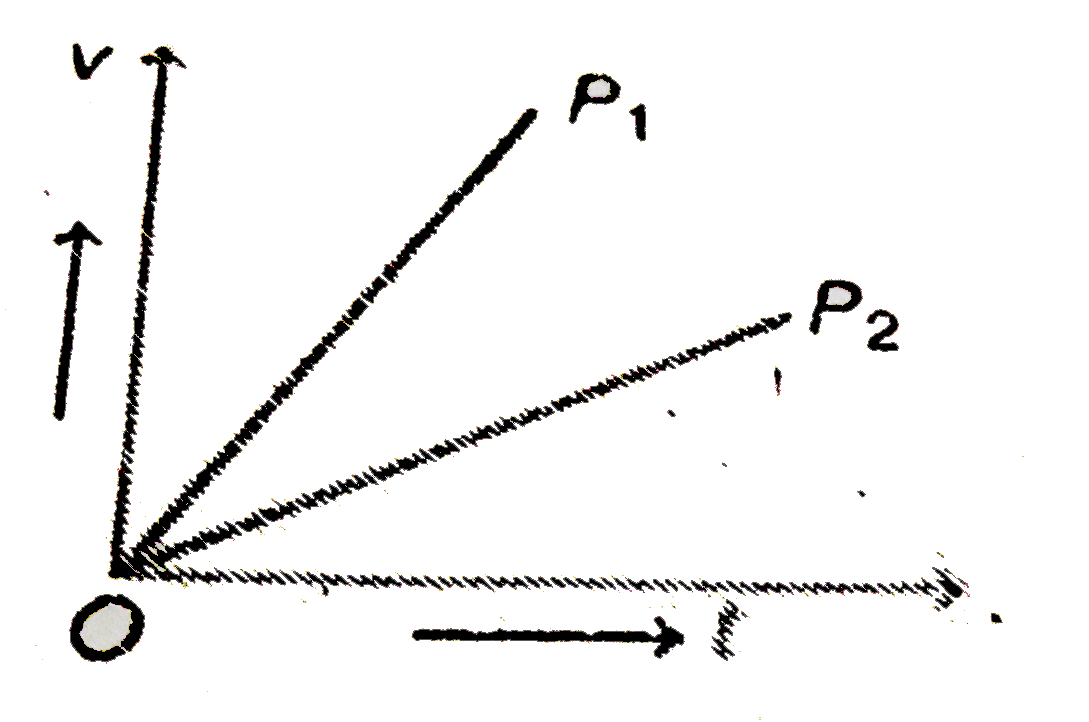
Their relative velocity
View SolutionA motorcylcle is moving with a velocity 80km/hr ahead of a car moving with a velocity of 65 km/hr in the same direction. What is the relative velocity of the motorcyle with respect ot the car:-
View SolutionTwo objects AandB are moving along the directions as shown in (Fig. 5.77). Find the magnitude and direction of the relative velocity of Bw.r.t.A.
 ,
,
View SolutionA car A is moving with speed 40 km h−1 along a straight line 30∘ north of east and another car B is moving with same speed along a straight line 30∘ south of east. The relative velocity of car A as observed from the car B is
View SolutionRain, driven by the wind, falls on a railway compartment with a velocity of 20ms−1, at an angle of 30∘ to the vertical. The train moves, along the direction of wind flow, at a speed of 108kmh−1. Determine the apparent velocity of rain for a person sitting in the train.
View SolutionTwo trains going in opposite directions with the same speed are at rest relative to each other. True/False.
View SolutionThe vector difference between the absolute velocities of two bodies is called their relative velocity. The concept of relative velocity enables us to treat one body as being at rest while the other is in motion with the relative velocity. This jormalism greatly simplifies many problems. If →vAis the absolute velocity of a body A and →–––(B)that of another body B then the relative velocity of A in relation to B is →–––(AD)=→VA−→vB and →vBA=→vB-→vA.
The principle follows here is that the relative velocity of two bodies remains unchaged if the same additional velocity is imparted to both the bodies. A simple way of carrying out this operation is to be represent the velocities in magnitude and direction from a common point. Then the line joining the tips of the vectors represents the relative velocity
Q A train A moves to the east with velocity of 40 km/hr and a train B moves due north with velocity of 30 km/hr. The relative velocity of A w.rt. B is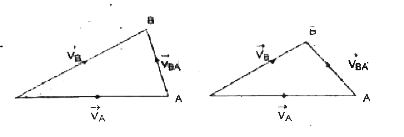
View SolutionTwo objects A and B are moving in opposite directions with velocities vAandvB respectively, the magnitude of relative velocity of A w.r.t. B is
View Solution
