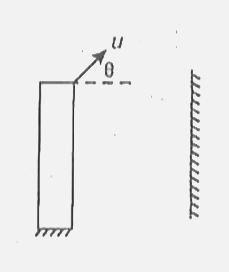
Ball $I$ is thrown towards a tower at an angle of $60^{\circ}$ with the horizontal with unknown speed $(u)$ . At the same moment, ball $I I$ is released from the top of tower as shown in (Fig. 5.189). Balls collide after $2 s$ and at the moment of collision, the velocity of ball $I$ is horizontal. Find the
(a) speed $u$
(b) distance of point of projection of ball $I$ from base of tower $(x)$
( c) height of tower
.

Video Solution

Text Solution

Verified by Experts

The correct Answer is:(a) $\frac{40}{\sqrt{3}} m s^{- 1}$ ;
(b) $\frac{40}{\sqrt{3}} m; c . 40 m$ .

(a) Time of ascent should be $2 s$ .
So $\frac{u {sin 60}^{\circ}}{g} = 2 \Rightarrow u = \frac{40}{\sqrt{3}} m s^{- 1}$
(b) $x = (u {cos 60}^{\circ}) t = \frac{40}{\sqrt{3}} \times \frac{1}{2} \times 2 = \frac{40}{\sqrt{3}} m$
( c) The height of tower can be found using concept of relative velocity. If the balls have to collide, the initial velocity of ball $I$ should be towards ball $I I$ .
For this $\frac{h}{x} = {tan 60}^{\circ} \Rightarrow h = x {tan 60}^{\circ} = \frac{40}{\sqrt{3}} \sqrt{3} = 40 m$
OR : height ascended by ball $I in 2 s$ :
$h_{1} = u {sin 60}^{\circ} \times 2 - \frac{1}{2} 10 {(2)}^{2} = 20 m$
height decended by ball $I I \in 2 s$ ,
$h_{2} = \frac{1}{2} {gt}^{2} = \frac{1}{2} 10 {(2)}^{2} = 20 m$
Now $h = h_{1} + h_{2} = 20 + 20 = 40 m$ .

|

Updated on:21/07/2023

Class 11 PHYSICS PROJECTILE MOTION

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
A ball $A$ is thrown up vertically with a speed $u$ and at the same instant another ball $B$ is released from a height $h$ . At time $t$ , the speed $A$ relative to $B$ is
Au
Bu - 2gt
C $\sqrt{u^{2} - 2 g h}$
Du - gt

CENGAGE PHYSICS ENGLISH-KINEMATICS-2-Exercise Subjective

Home
Ask Doubt
Profile