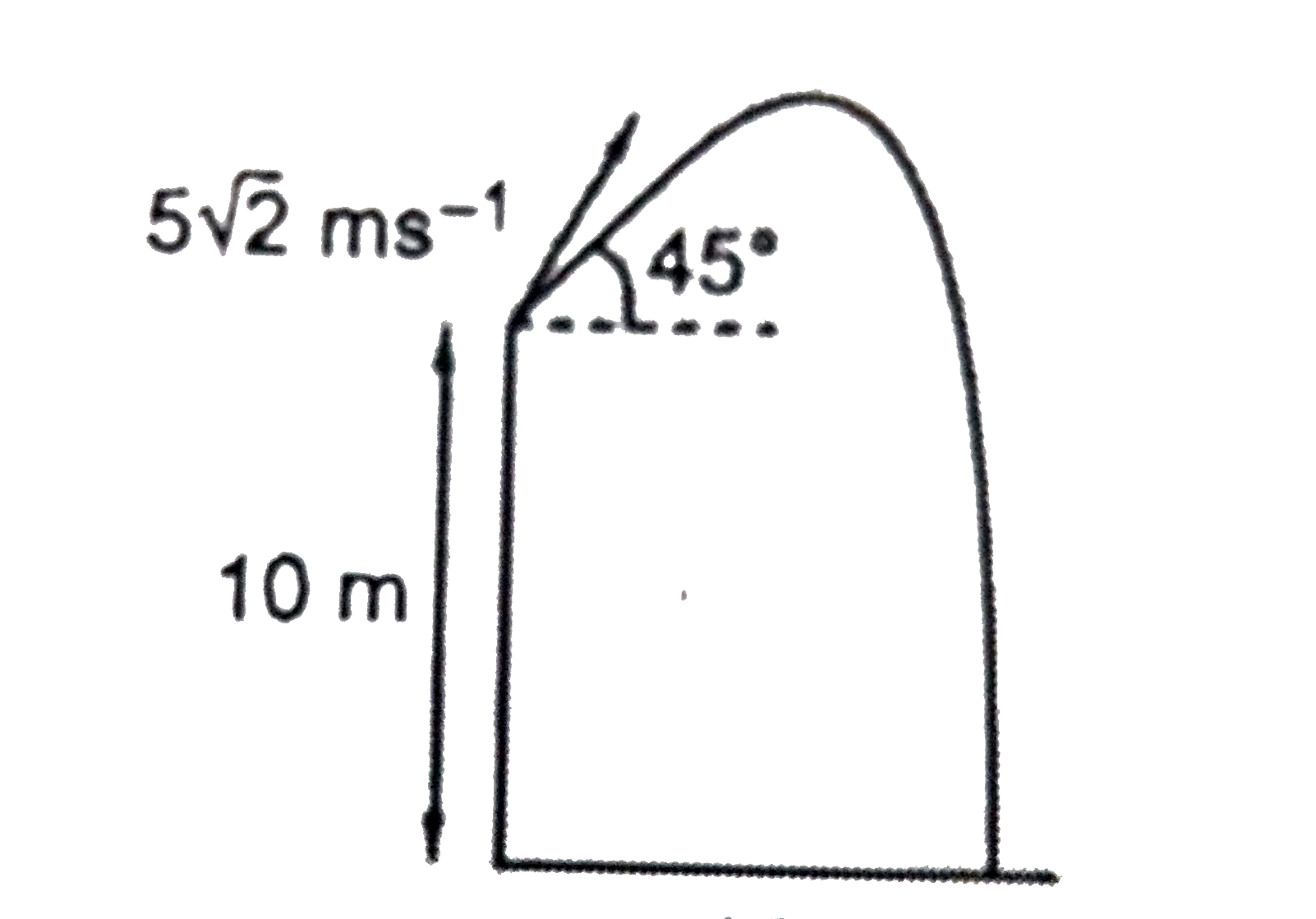
A particle is projected from point A to hit an apple as shown in (Fig. 5.195). The particle is directly aimed at the apple. Show that particle will not hit the apple. Now show that if the string with which the apple is hung is cut at the time of firing the particle, then the particle will hit the apple.
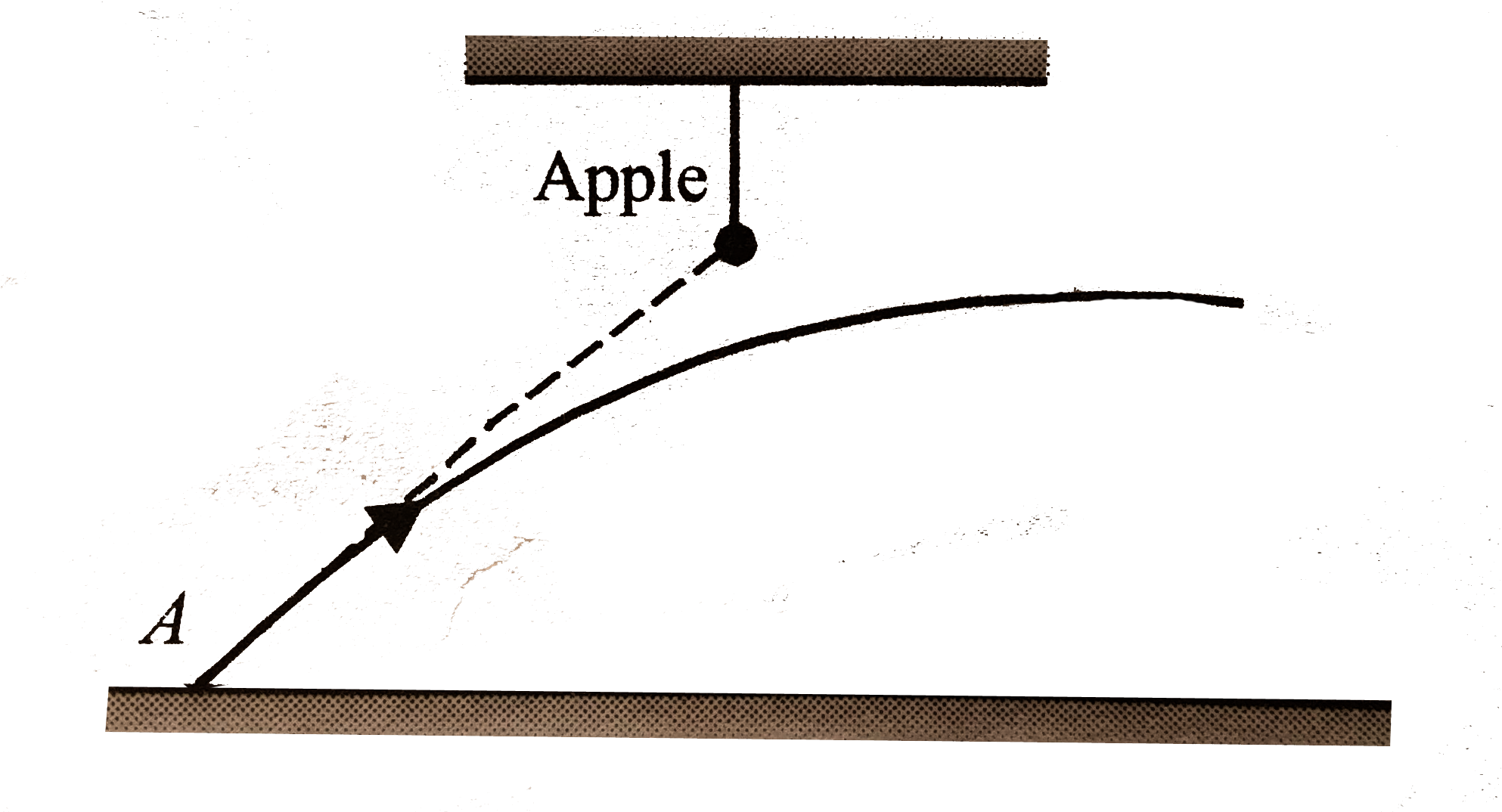 .
.
The apple will not fall in the path of the trajectory of the particle. Hence, the particle will not hit the apple. But when the string is cut, the vertical fall of apple and the particle will be equal. Hence the particle willl hit apple.
Topper's Solved these Questions
- KINEMATICS-2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-2EXERCISE - Exercise Single Correct
76 Videos
- KINEMATICS-2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-2EXERCISE - Exercise Multiple Correct
11 Videos
- KINEMATICS-2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-2EXERCISE - Exercise 5.4
11 Videos
- KINEMATICS-1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-1EXERCISE - Integer
9 Videos
- KINETIC THEORY OF GASESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINETIC THEORY OF GASESEXERCISE - Compression
2 Videos
Similar Questions
Knowledge Check
A particle is projected on an inclined plane with a speed u as shown in (Fig. 5.61). Find the range of the particle on the inclined plane.
 .A2u2√3+13g.B4u2√3−19g.C2u2√5−18g.D2u2√3−13g
.A2u2√3+13g.B4u2√3−19g.C2u2√5−18g.D2u2√3−13gParticle is projected from the ground at a certain angle with horizontal . If particle takes time T to hit the ground again , then maximum height of the projectile is
AT2g2BT2g4CT2g8DT2g5Deflection back of a few particles on hitting thin foil of gold shows that
Anucleus is heavyBnucleus is smallCBoth a and bDeletrons create hindrance in the movement of α−partic≤s
Two particles are separated at a horizontal distance x as shown in (Fig. 5.57). They are projected at the same time as shown in the figure with different initial speed. Find the time after which the horizontal distance between the particles becomes zero.
 .
.
View SolutionTwo particles are separated at a horizontal distance x as shown in (Fig. 5.57). They are projected at the same time as shown in the figure with different initial speed. Find the time after which the horizontal distance between the particles becomes zero.
 .
.
View SolutionA particles is projected horizontally with a speed v from the top of a plane inclined at an angle tehta to the horizontal as shown in the figure.
(a) Hwo far from the point of projection will the particle strike the plane ?
(b) Find the time taken by the particel to hit the plane.
(c) What is the velocity of particle just before it hits the plane ?
View SolutionA particles is projected horizontally with a speed v from the top of a plane inclined at an angle tehta to the horizontal as shown in the figure.
(a) Hwo far from the point of projection will the particle strike the plane ?
(b) Find the time taken by the particel to hit the plane.
(c) What is the velocity of particle just before it hits the plane ?
View SolutionA pillar having square cross section of side length L is fixed on a smooth floor. A particle of mass m is connected to a corner A of the pillar using an inextensible string of length 3.5 L. With the string just taut along the line BA, the particle is given a velocity v perpendicular to the string. The particle slides on the smooth floor and the string wraps around the pillar.
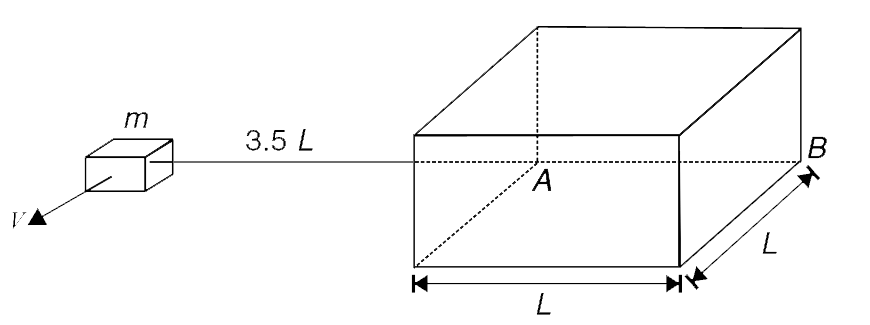
(a) Find the time in which the particle will hit the pillar. (b) Find the tension in the string just before the particle hits the pillar. Neglect any energy loss of the particle.
View Solution