A man wants to reach point B on the opposite bank of a river flowing at a speed as shown in figure. What minimum speed and in which direction should the man swim relative to water so that he can reach point B ?
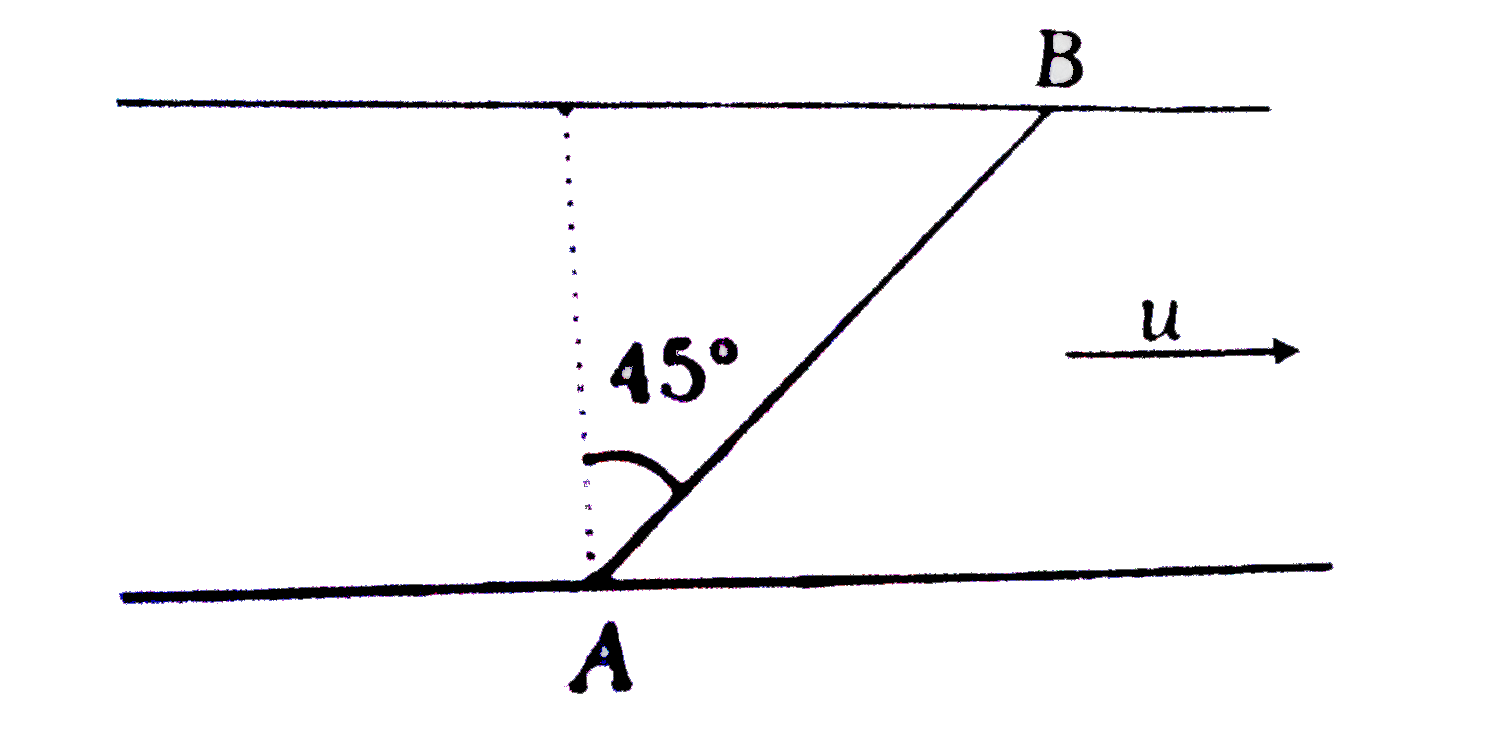
The correct Answer is:u√2,45∘ with upstream.
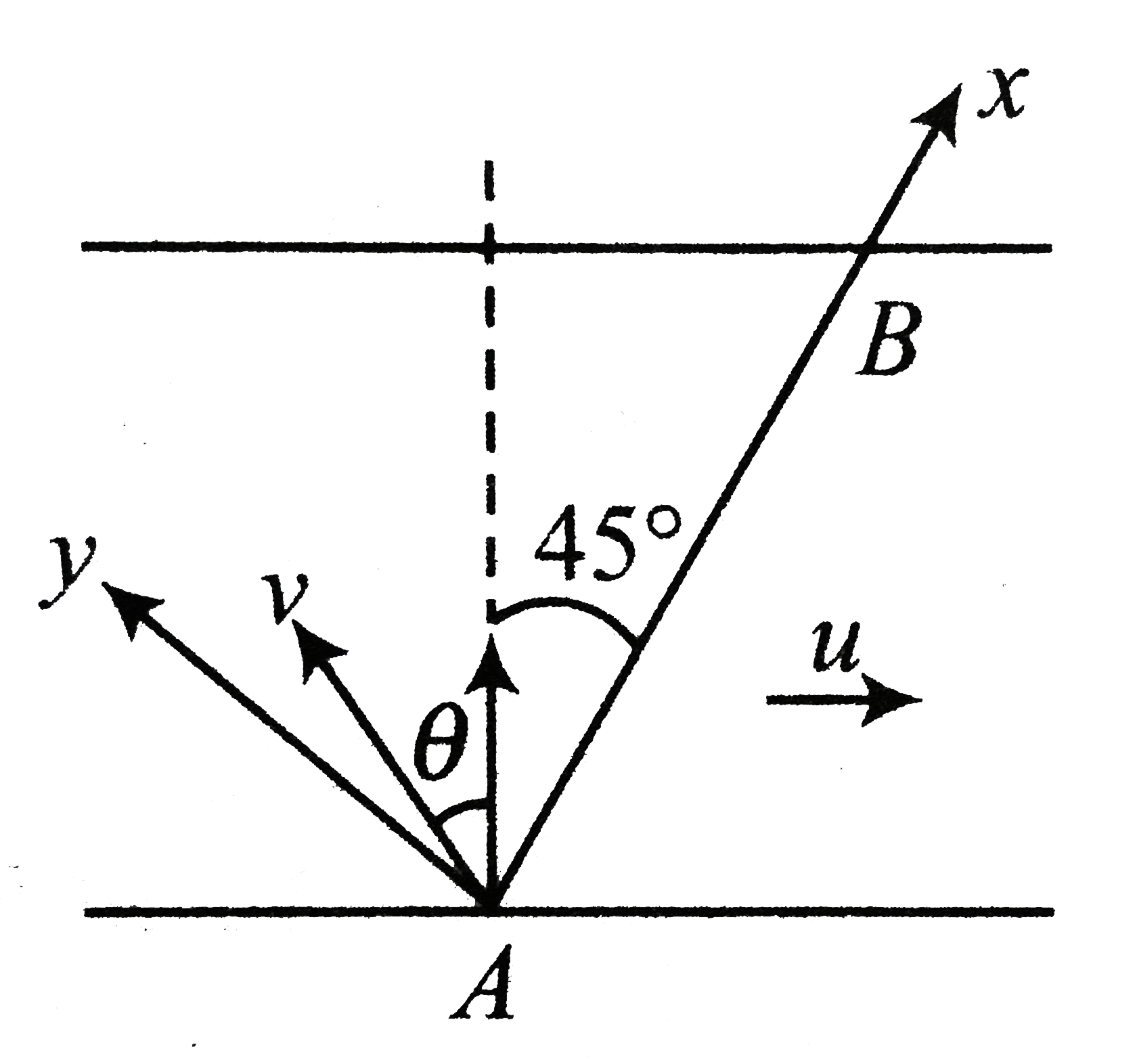
→vm=→vm/w+→vw=vcos(θ+45∘)ˆi+vsin(θ+45∘)ˆj
+ucos45∘ˆi−usin45dˆj=[vcos(θ+45∘)+ucos45∘]ˆi
+[vsin(θ+452−usin45∘]ˆj
To reach the point B, ˆj component should be zero
vsin(θ+45∘)=usin45∘
⇒v=usin45∘sin(θ+45∘)
For vmin,θ+45∘=90∘⇒θ=45∘
⇒vmin=u√2,45∘ with upstream.
 .
.
Topper's Solved these Questions
- KINEMATICS-2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-2EXERCISE - Exercise Single Correct
76 Videos
- KINEMATICS-2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-2EXERCISE - Exercise Multiple Correct
11 Videos
- KINEMATICS-2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-2EXERCISE - Exercise 5.4
11 Videos
- KINEMATICS-1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-1EXERCISE - Integer
9 Videos
- KINETIC THEORY OF GASESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINETIC THEORY OF GASESEXERCISE - Compression
2 Videos
Similar Questions
A man wants to reach point B on the opposite bank of a river flowing at a speed as shown in figure. What minimum speed relative to water should the man have so that he can reach point B? In which direction should he swim?
View SolutionGiven |Vbr|=4m/s= magnitude of velocity of boatman with respect to river, vr=2m/s in the directior shown. Boatman wants to reach from point A to point B. At what angle θ should he row his boat ?
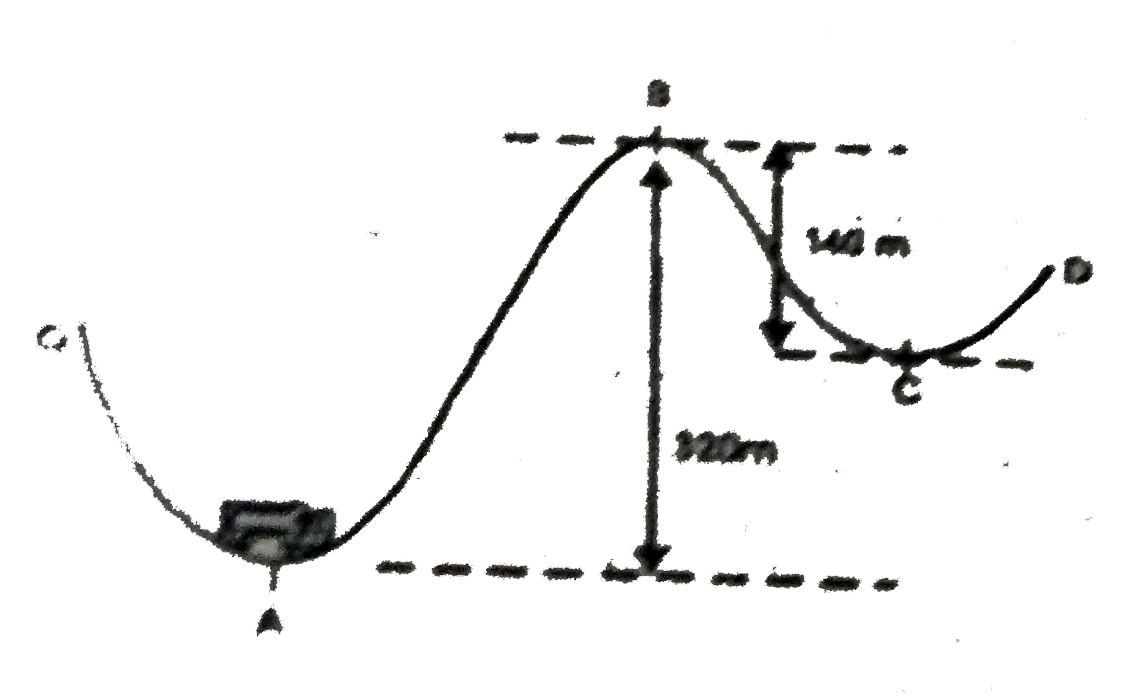
View SolutionTrack OABCD (as shown in figure ) is smooth. What minimum speed has to be given to a particle lying at point A, so that it can reach point C? (take g=10m/s2)
View SolutionIf speed of water in river is 4 m/s and speed of swimmer with respect to water is 3 m/s, then in which direction the swimmer must swim so that he will reach directly opposite end?
View SolutionA swimmer starts to swim from point a to cross a river. He wants to reach point B on the opposite side of the river. The line AB makes an angle 60∘ with the river flow as shown. The velocity of the swimmer in still water is same as that of the water
(i) In what direction should he try to direct his velocity ? Calculate angle between his velocity ? Calculate angle between his velocity and river velocity.
(ii) Find the ratio of the time taken to cross the river in this situation to the minimum time in which he can cross this river.

View SolutionIn the figure shown a river of width 4m is flowing with speed of 5m/s. A swimmer whose swimming speed relative to the water is 4ms, starts swimming from a point A on a bank. On the other bank B is a point which is directly opposite to A. What minimum distance (in m) the swimmer will have to walk on the other bank to reach the point B.
View SolutionA boat man can row with a speed of 10kmh−1 in still water. If the river flows steadily at 5km/h, in which direction should the boatman row in order to reach a point on the other bank directly opposite to the point from where he stared ? The width of the river is 2km.
View SolutionA person aiming to reach exactly opposite point on the bank of a stream is swimming with a speed of 0.6 m/s at an angle of 120∘ with the direction of flow of water . The speed of water in the stream is
View SolutionA man who can swim at a velocity v relative to water wants to cross a river of width b, flowing with a speed u.
View SolutionA man who can swim at a velocity v relative to water wants to cross a river of width b, flowing with a speed u.
View Solution
