Ship A is travelling with a velocity of 5kmh−1 due east. A second ship is heading 30∘ east of north. What should be the speed of second ship if it is to remain always due north with respect to the first ship ?
a. 10kmh−1
b. 9kmh−1
c. 8kmh−1
d. 7kmh−1
The correct Answer is:A
To solve the problem, we need to determine the speed of the second ship (Ship B) such that it always remains due north with respect to the first ship (Ship A), which is moving due east.
1. Identify the velocities:
- Let the velocity of Ship A (V_A) = 5 km/h (due east).
- Let the velocity of Ship B (V_B) be at an angle of 30° east of north.
2. Break down the velocity of Ship B into components:
- The northward component of Ship B's velocity (V_B_north) = V_B * cos(30°).
- The eastward component of Ship B's velocity (V_B_east) = V_B * sin(30°).
3. Establish the condition for Ship B to remain due north of Ship A:
- For Ship B to remain due north of Ship A, the eastward component of Ship B's velocity must equal the velocity of Ship A. Thus, we have:
VB⋅sin(30°)=VA
- Substituting the known value of V_A:
VB⋅sin(30°)=5 km/h
4. Calculate sin(30°):
- We know that sin(30°) = 1/2.
5. Substitute sin(30°) into the equation:
VB⋅12=5
6. Solve for V_B:
- Multiply both sides by 2:
VB=5⋅2=10 km/h
Conclusion:
The speed of the second ship (Ship B) should be 10 km/h to remain always due north with respect to the first ship (Ship A).
---
- Let the velocity of Ship A (V_A) = 5 km/h (due east).
- Let the velocity of Ship B (V_B) be at an angle of 30° east of north.
- The northward component of Ship B's velocity (V_B_north) = V_B * cos(30°).
- The eastward component of Ship B's velocity (V_B_east) = V_B * sin(30°).
- For Ship B to remain due north of Ship A, the eastward component of Ship B's velocity must equal the velocity of Ship A. Thus, we have:
VB⋅sin(30°)=VA
- Substituting the known value of V_A:
VB⋅sin(30°)=5 km/h
- We know that sin(30°) = 1/2.
VB⋅12=5
- Multiply both sides by 2:
VB=5⋅2=10 km/h
The speed of the second ship (Ship B) should be 10 km/h to remain always due north with respect to the first ship (Ship A).
Topper's Solved these Questions
- KINEMATICS-2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-2EXERCISE - Exercise Multiple Correct
11 Videos
- KINEMATICS-2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-2EXERCISE - Exercise Assertion - Reasoning
5 Videos
- KINEMATICS-2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-2EXERCISE - Exercise Subjective
40 Videos
- KINEMATICS-1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-1EXERCISE - Integer
9 Videos
- KINETIC THEORY OF GASESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINETIC THEORY OF GASESEXERCISE - Compression
2 Videos
Similar Questions
A ship is travelling due east at a speed of 15km/h. Find the speed of a boat heading 30∘ east of north if it appears always due north from the ship.
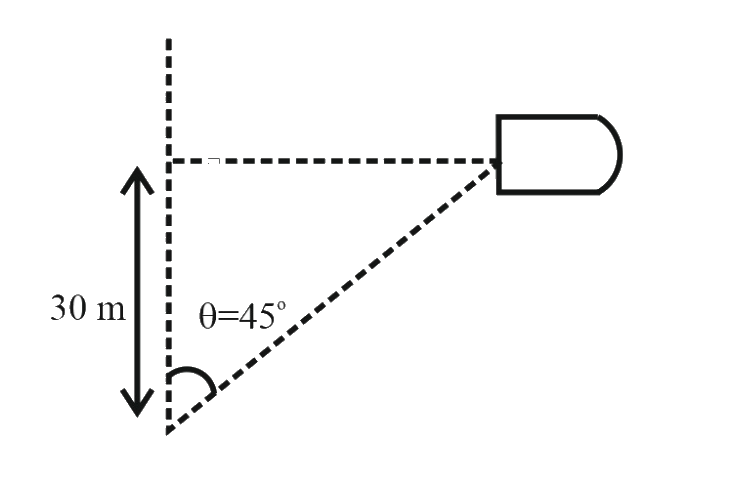
View SolutionA boat is travelling with a speed of 27 km h−1 due east. An observer is situated at 30 m south of the line of travel. The angular velocity of the boat relative to be the observer in the position shown will be
View SolutionA car is moving with a speed of 25 km/hour in the East. A bus is moving with a speed of 25√3 km/hour in the North. What will be the relative velocity of the bus for the car's driver ?
View SolutionAnoop is moving due east with a velocity of 1m/s and Dhyani is moving due west with a velocity of 2m/s. what is the velocity of Anoop with respect to Dhyani?
View SolutionA man travelling towards east at 8km/h finds that the wind seems to blow directly from the north On doubling the speed, he finds that it appears to come from the north-east. Find the velocity of the wind.
View SolutionA bird is fying due east with a velocity of 4ms−1. The starts to blow with a velocity of 3ms−1 due north. What is the magnituide of relative velocity of bird w.r.t. wind ? Find out its direction also.
View SolutionShip A is 10km due west of ship B. Ship A is heading directly north at a speed of 30 kmph while ship B is heading in a direction 60° west of north at a speed 20kmph. Their closest distance of approach will be........
View SolutionShip A is located 4 km north and 3 km east of ship B. Ship A has a velocity of 20kmh−1 towards the south and ship B is moving at 40kmh−1 in a direction 37∘ north of east. X and Y-axes are along east and north directions, respectively
View SolutionA Ship A steams down north at a speed of 8 kmph. and ship B due west at a speed of 6 kmph. The velocity of A w.r.t. B is.
View SolutionA truck travelling due North at 50kmh−1 turns West and travels at the same speed. What is the change in velocity ?
View Solution