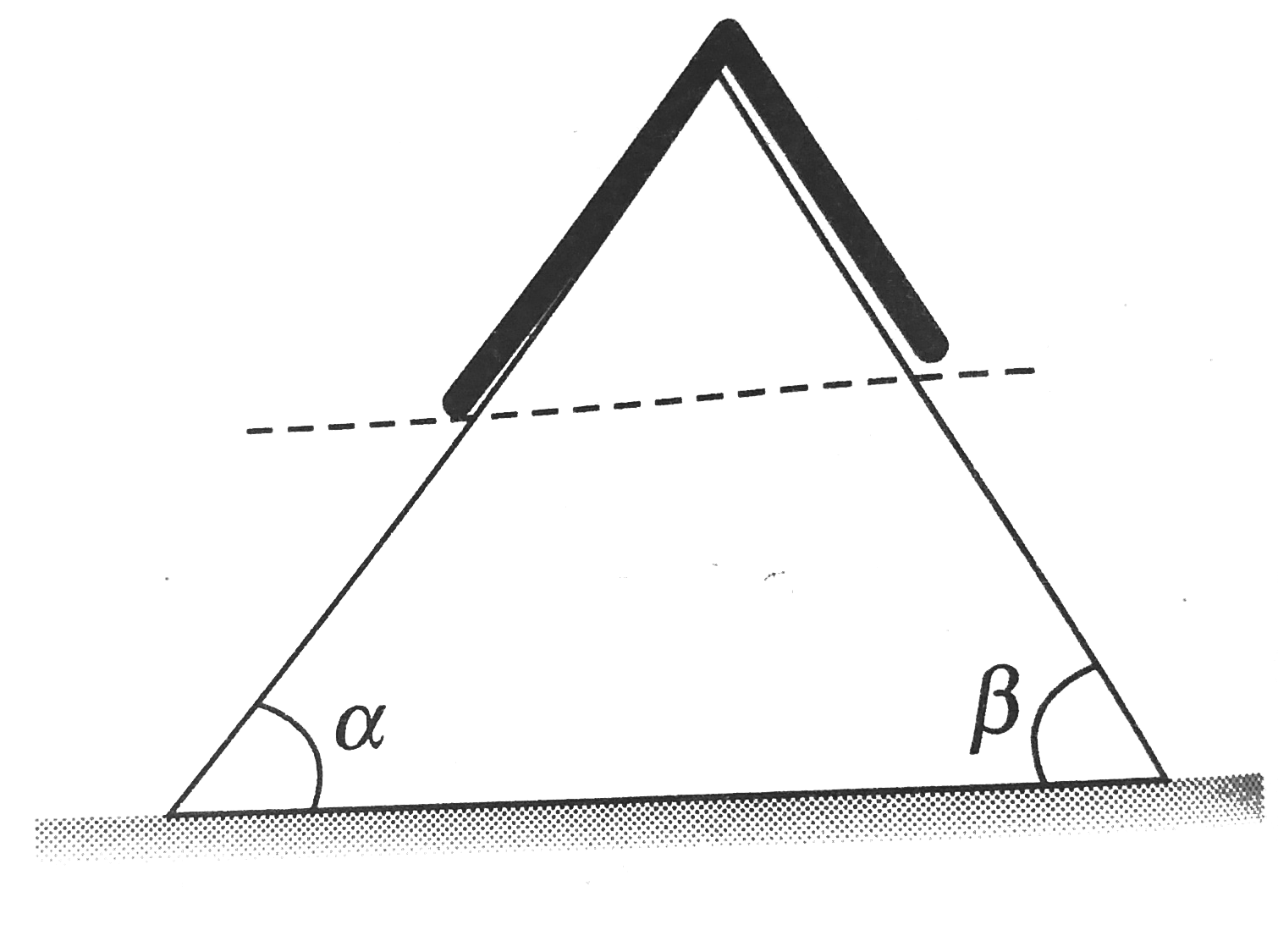
A homogeneous flexible rope rests on a wedge whose side edges make angles α and β with the horizontal. The central part of the rope lies on the upper rib C of the wedge. With what acceleration should the wedge be pulled to the left along the horizontal plane in order to prevent the displacement of the rope with respect to the wedge? [Consider all surfaces to be smooth]
![A homogeneous flexible rope rests on a wedge whose side edges make angles alpha and beta with the horizontal. The central part of the rope lies on the upper rib C of the wedge. With what acceleration should the wedge be pulled to the left along the horizontal plane in order to prevent the displacement of the rope with respect to the wedge? [Consider all surfaces to be smooth]](https://d10lpgp6xz60nq.cloudfront.net/physics_images/BMS_V01_C06_S01_020_Q01.png)
Consider the parts of rope on either size of incline as two different elements. Draw FBD. Apply Newton's law on these parts separately
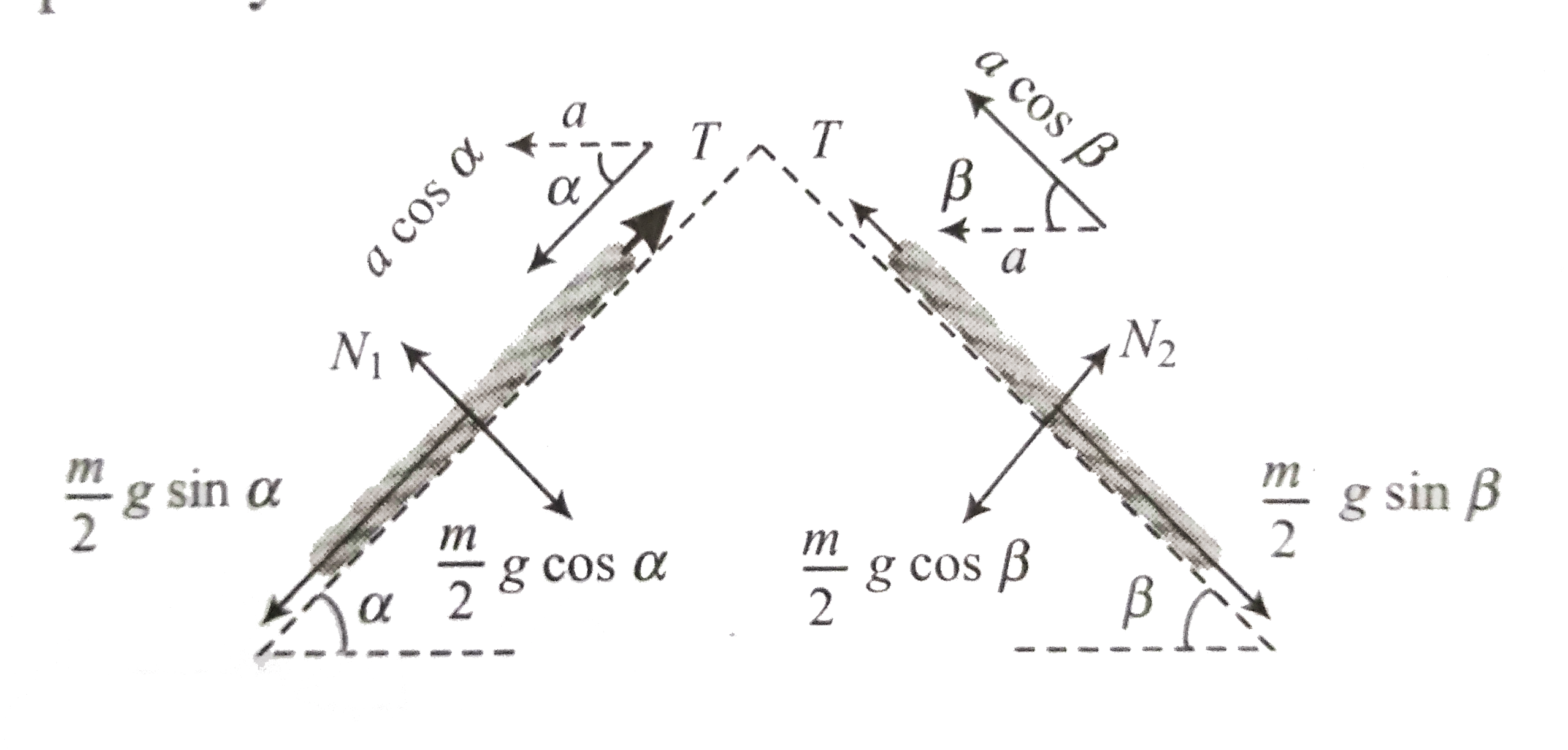
Taking components of acceleration along incline surface,
For left side part of rope: mg2sinα−T=m2acosα
For right side part of rope: T−mg2sinβ=m2acosβ
On solving, we get a=g[sinα−sinβ]cosβ+cosα.
Topper's Solved these Questions
- NEWTON'S LAWS OF MOTION 1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Solved Examples
11 Videos
- NEWTON'S LAWS OF MOTION 1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Exercise 6.1
11 Videos
- MISCELLANEOUS VOLUME 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 2EXERCISE - INTEGER_TYPE
10 Videos
- NEWTON'S LAWS OF MOTION 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Integer type
1 Videos
Similar Questions
A small block of mass m rests on a smooth wedge of angle θ. With what horizontal accelaration a should the wedge be pulled, as shown in fig, so that the block falls freely?
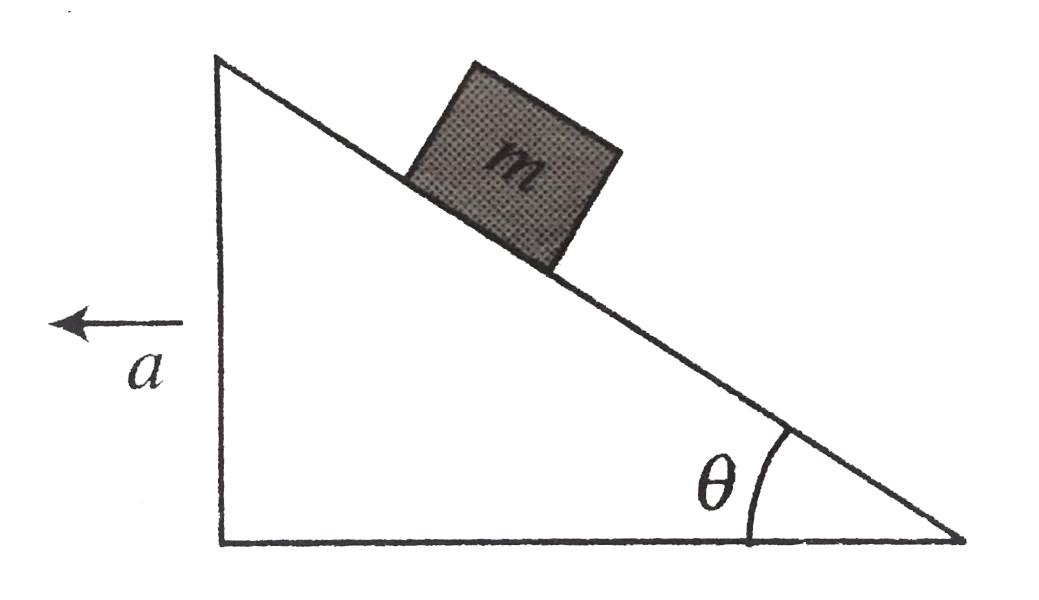
View SolutionA small block of mass m rests on a smooth wedge of angle θ. With what horizontal accelaration a should the wedge be pulled, as shown in fig, so that the block falls freely?

View SolutionA weightless inextensible rope rests on a stationary wedge forming an angle α with a horizontal One end of the rope is fixed to the wall to point A.A small load is attached to the rope at point B The wedge starts moving to the right with a constant acceleration a The acceleration of the load is given by
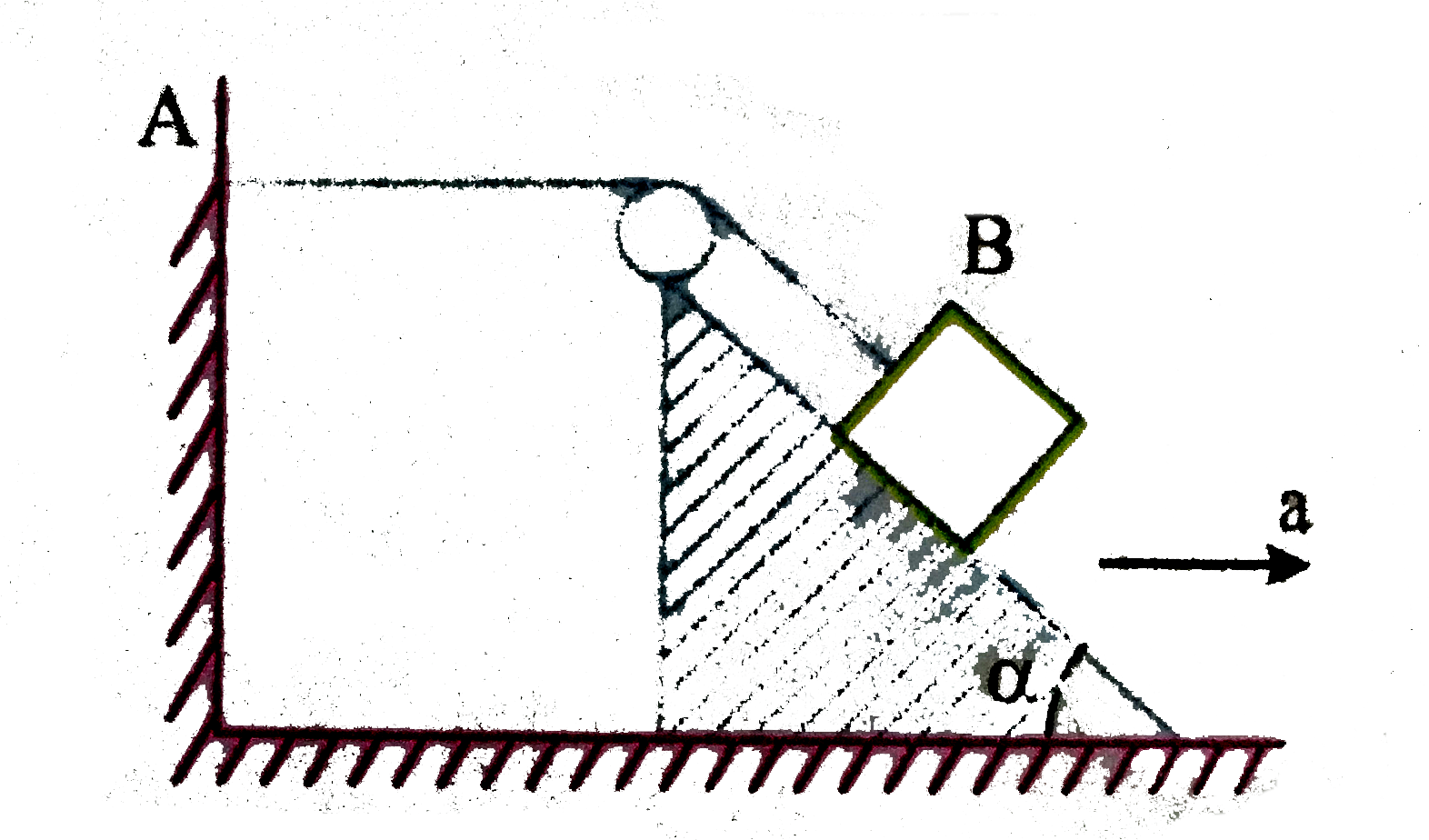 .
.
View Solution
A block is placed on a smooth wedge of inclination angle θ with the horizontal. What minimum acceleration should be given to the wedge in the horizontal direction so that the block starts moving up along the incline?
View SolutionA block of mass m is placed on an inclined plane. With what acceleration A towards right should the system move on a horizontal surface so that m does not slide on the surface of inclined plane? Also calculate the force supplied by wedge on the block. Assume all surfaces are smooth.
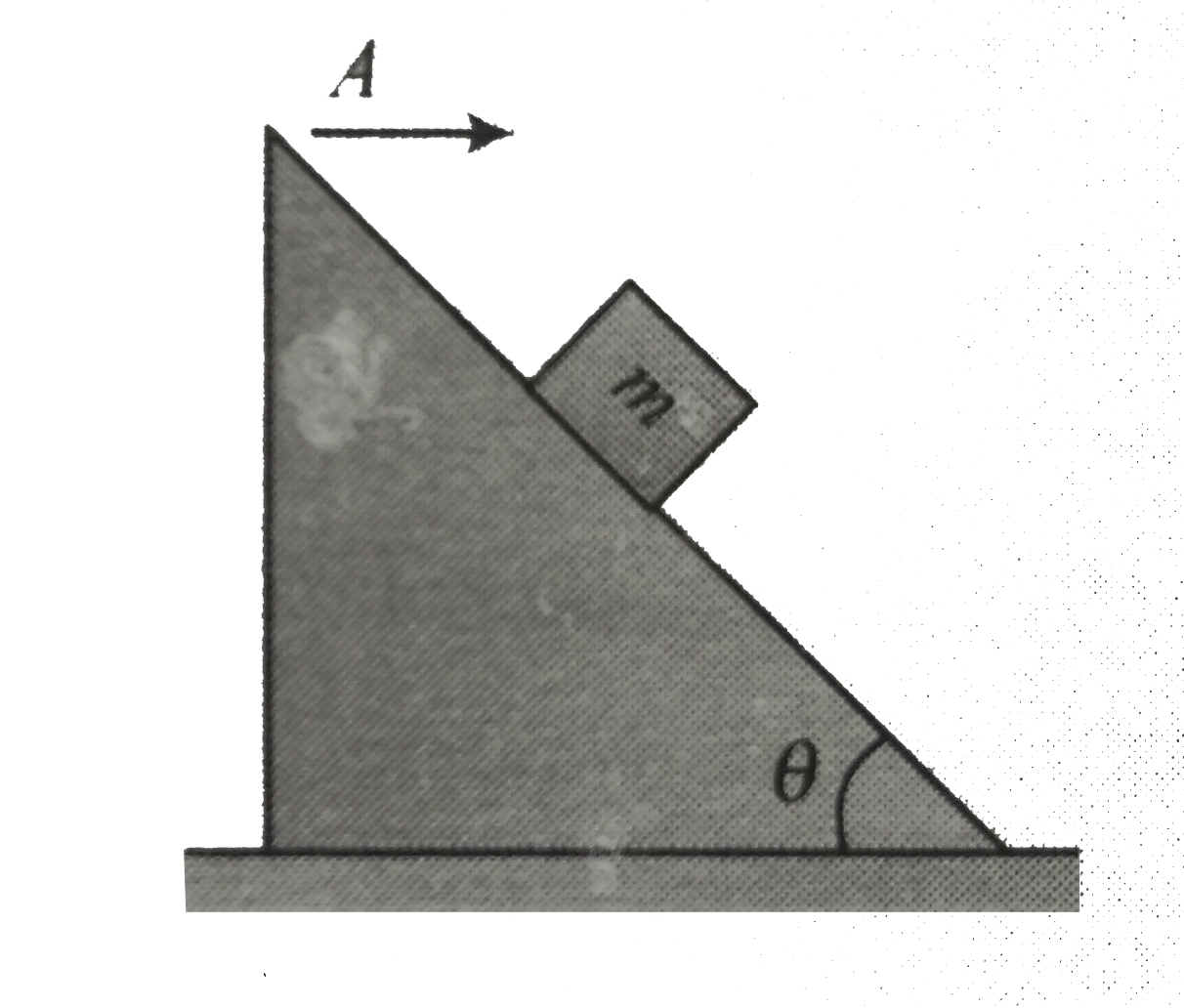
View SolutionA block of mass m is placed on an inclined plane. With what acceleration A towards right should the system move on a horizontal surface so that m does not slide on the surface of inclined plane? Also calculate the force supplied by wedge on the block. Assume all surfaces are smooth.

View SolutionA uniform of rope length L and mass M is placed on a smooth fixed wedge as shown. Both ends of rope are at same horizontal level. The rope is initially released from rest, then the magnitude of initial acceleration of rope is.
View Solution
A wedge of mass M=10kg, height h=3m and angle of inclination α=37∘ is at rest at horizontal surface. There is a small point -like object (mass m=0.5kg) next to the slope as shown in the figure. At what acceleration musts wedge be moved in order that the point like object reaches its top in a time t=5s (neglect the friction between point like object and wedge)
View SolutionA rectangular box lies on a rough inclined surface . The coefficient of friction between the surface and the box is μ. Let the mass of the box be m .
(a) At what angle of inclination θ of the plane to the horizontal will the box just start to slide down the plane ?
(b) What is the force acting on the box down the plane , if the angle of inclination of the plane is increased to α>θ ?
(c) What is the force needed to be applied upwards along the plane to make the box either remain stationary or just move up with uniform speed ?
(d) What is the force needed to be applied upwards along the plane to make the box move up the plane with acceleration a ?
View SolutionA block of mass M is tied to one end of a massless rope. The other end of the rope is in the hands of a man of mass 2M as shown in Fig. The block and the man art resting on a rough wedge of mass M. The whole system is resting on a smooth horizontal surface. The man starts walking towards right while holding the rope in his hands. Pulley is massless and frictionless. Find the displacement of the wedge when the block meets the pulley. Assume wedge is sufficiently long so that man does not fall down.

View Solution
