A pulley-rope-mass arrangement is shown in fig. Find the acceleration of block m1 when the masses are set free to move. Assume that the pulley and the ropes are ideal.
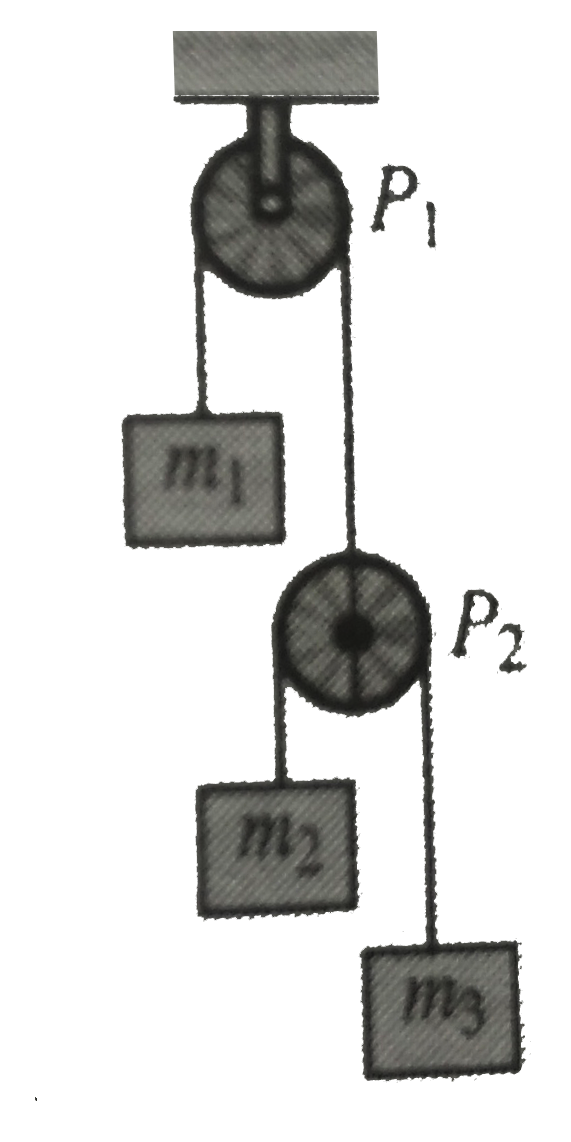
Constraint relations Method 1:
For the upper string, the length of string l1 not to change and for this string not to slacken, acceleration of m1 w.r.t. the fixed pulley = acceleration of the movable pulley w.r.t. the fixed pulley
or |a1|=|aP| ..(i)
Constraint relations for string 2
Let us assume that block m1 is moving down with acceleration a2 and a3 , respectively w.r.t. ground
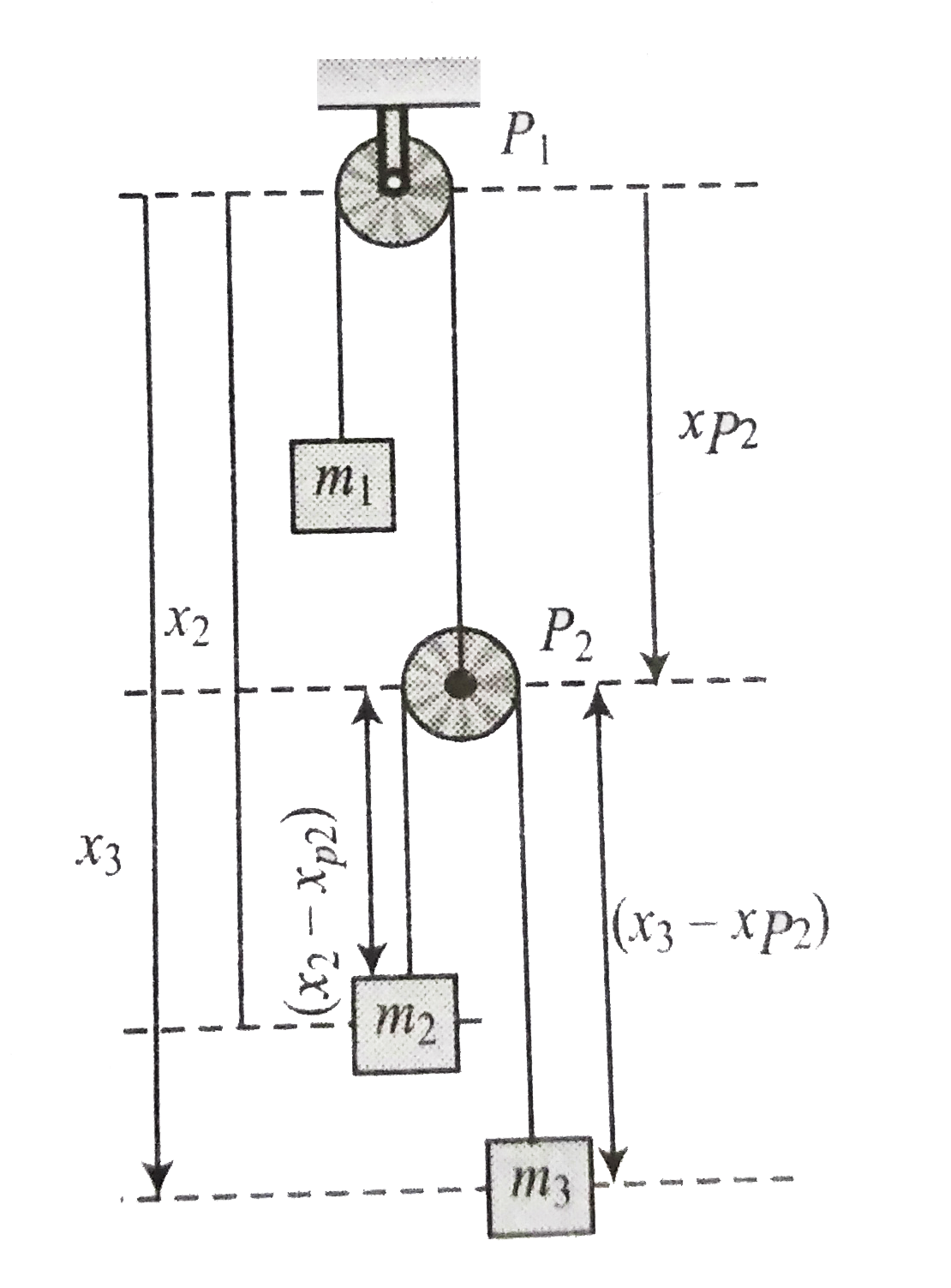
Total length of string 2 is constant. Therefore,
l2=(x2−xp2)+(x3−xp2)+l'0
where l0 is the length of string on pulley 2 passing through the pulley P2
l2=x2+x3−2xP2+l'0...(ii)
Differentiating Eq. (ii) w.r.t. time
dl2dt=0 (as total length of string is constanat)
dl'0d=0 (as length of string over pulley is constant)
differentiating eq.(ii) twice w.r.t. time
2a1=a3+a2 ..(iii)
Method 2: The acceleration of block m1 and pulley 2 will be same in magnitude. Now considering pulley 2 and block 2 and 3.
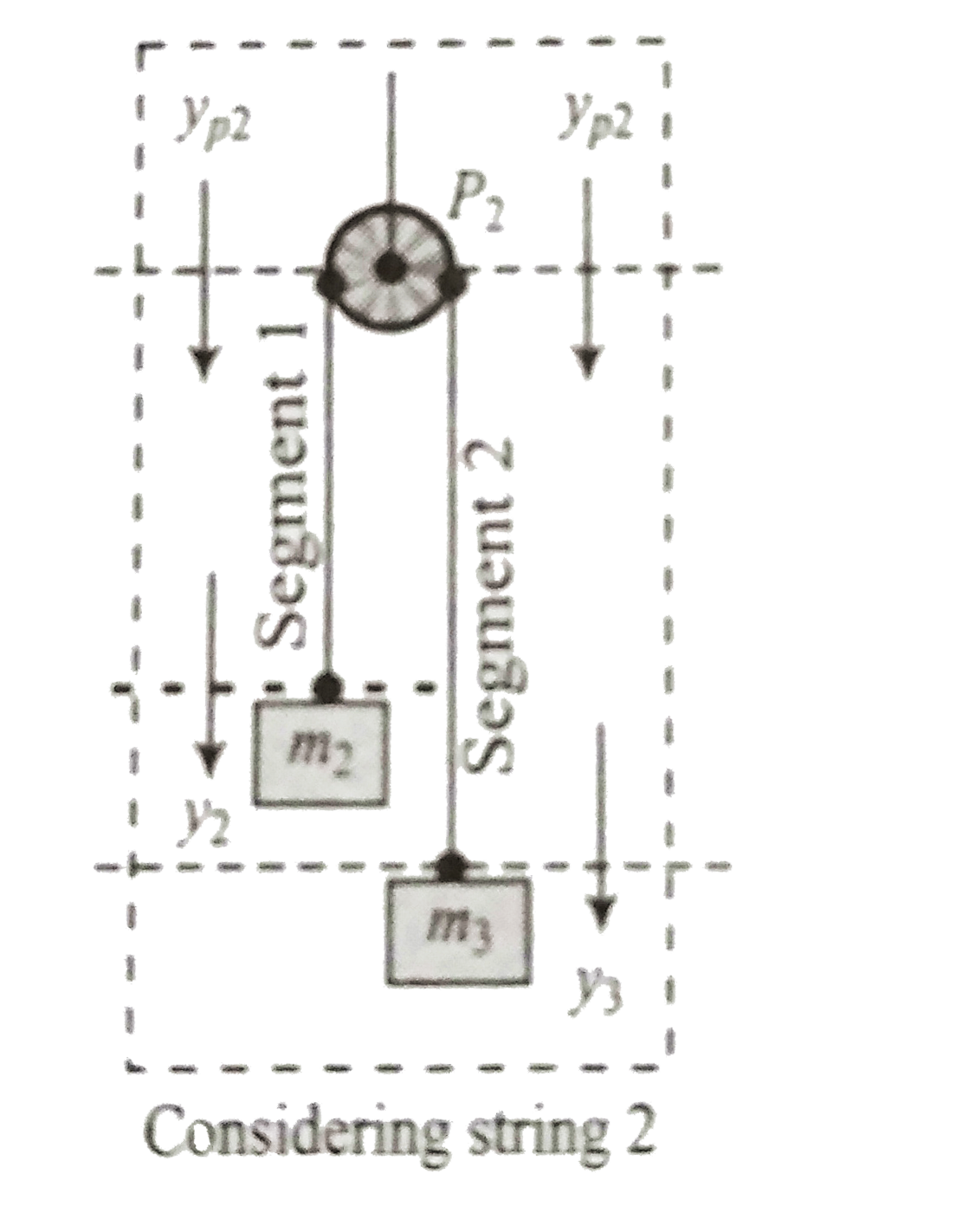
Change in the length of segment (1)
Δl1=(+y2)+(−yP2)=y2−yp2
Change in the length of segment (2)
Δl2=(y3)+(−yp2)=y3−yP2
Total sum of change in the segment length of string should be zero.
Δl=0=[y2−yP2]+[y2−yP2]
⇒Δl=0=y2+y3−2yP2
⇒2yp2=y3+y2⇒2ap2=a3+a2
or 2a1=a3+a2
This equation is same as (iii) calculate in method (2) .
Method 3: For the rope length l2 not to change and for this rope not to slacken acceleration of m2 w.r.t movable pully =-acceleration of m3w.r.t. movable pullwy
or (a2−ap)=−(a3−ap)
a2+a3−2ap=0⇒2a0=a2+a3
This equation is same as Eq.(iii) as calucutate in method 1 and 2
Applying Newton's laws of motion equations.
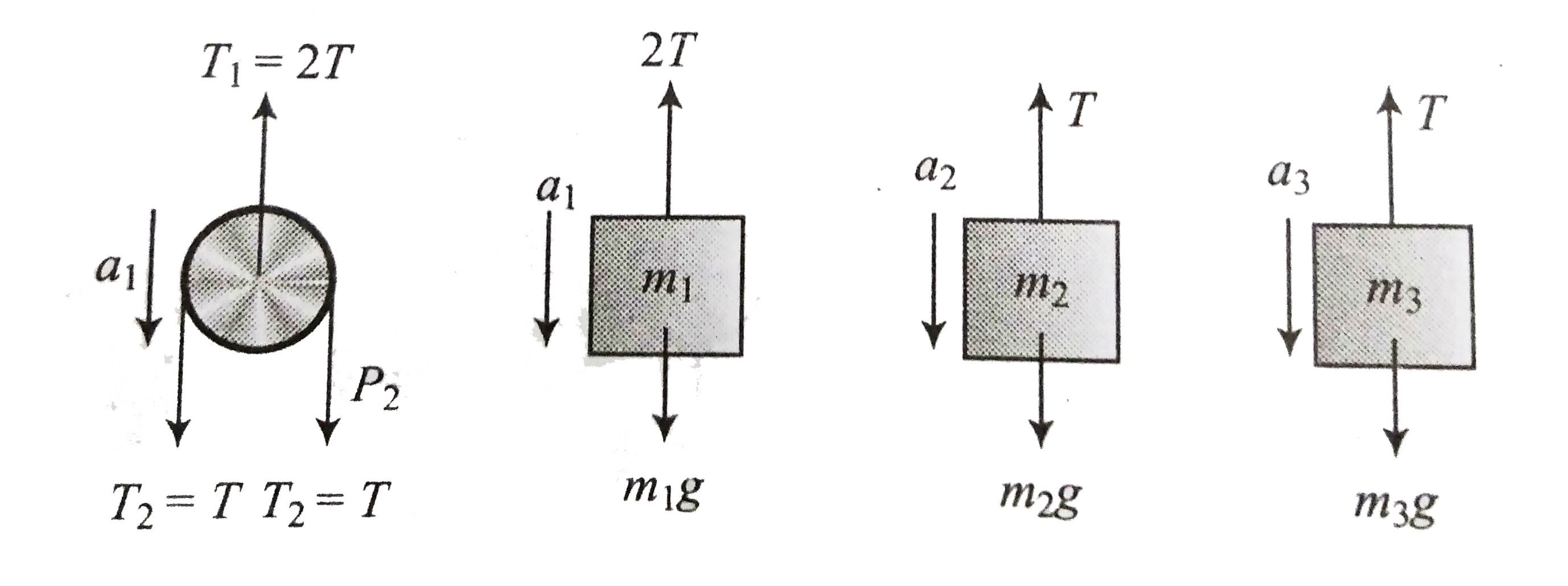
Free body diagram
Equation of motion
for m1:2T−m1g=m1a1 ...(iv)
for m2:m2g−T=m2a2...(v)
for m3:m3g−T=m3a3...(vi)
After solving (iii),(iv), (v), and (vi), we get
a1=4m2m3g−m1(m2+m3)g4m2m3+m1(m2+m3).
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Solved Examples11videos
NEWTON'S LAWS OF MOTION 1
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Exercise 6.111videos
NEWTON'S LAWS OF MOTION 1
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 2EXERCISE - INTEGER_TYPE10videos
MISCELLANEOUS VOLUME 2
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Integer type1videos
NEWTON'S LAWS OF MOTION 2
Similar Questions
In the pulley-block arrangement shown in figure , find the relation between acceleration of blocks A and B
 View Solution
View SolutionIn the pulley-block arrangement shown in figure , find the relation between acceleration of blocks A and B
 View Solution
View SolutionFind the acceleration of blocks in fig. The pulley and the string are massless.
 View Solution
View SolutionFor given system as shown in figure, the acceleration of block of mass m(m=M/2) kept on smooth table when the system is released from rest is (Strings and pulleys are ideal)
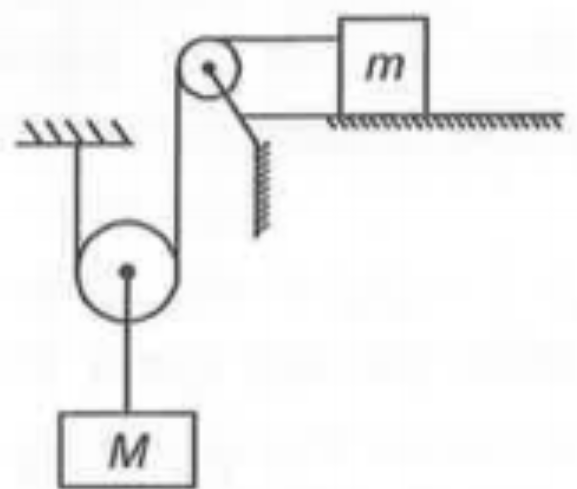 View Solution
View SolutionThe velocities of A and B shown in fig. Find the speed (in ms−1) of block C. (Assume that the pulleys and string are ideal).
 View Solution
View SolutionFor given system as shown in figure, the acceleration of block of mass m(m=M2) kept on smooth table when the system is released from rest is (Strings and pulleys are ideal)
View SolutionIn the arrangement shown, the mass m will ascend with an acceleration ( Pulley and rope are massless)
 View Solution
View SolutionIn the arrangement shown, the mass m will ascend with an acceleration ( Pulley and rope are massless)
 View Solution
View Solutionfind the acceleration of the block of mass M in the situation shown in figure. All the surfaces are frictionless and the pulleys and the string are light.
 View Solution
View SolutionA block of mass m=5kg is placed on the wedge of mass M=32kg as shown in the figure. Find the acceleration of wedge with respect to ground. (Neglect any type of friction. Spring and pulley are ideal)
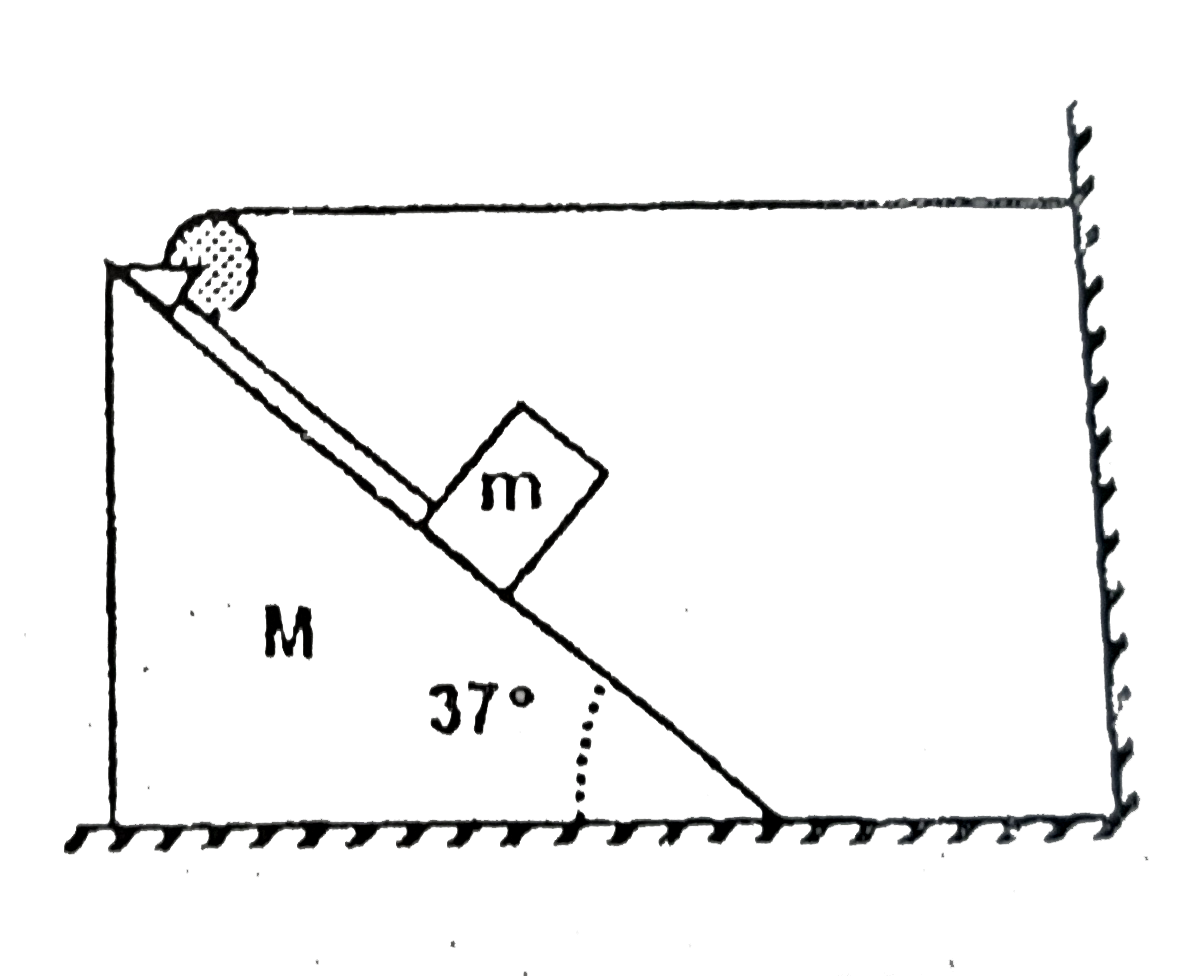 View Solution
View Solution

