A pulley-rope-mass arrangement is shown in fig. Find the acceleration of block $m_{1}$ when the masses are set free to move. Assume that the pulley and the ropes are ideal.

Video Solution

Text Solution

Verified by Experts

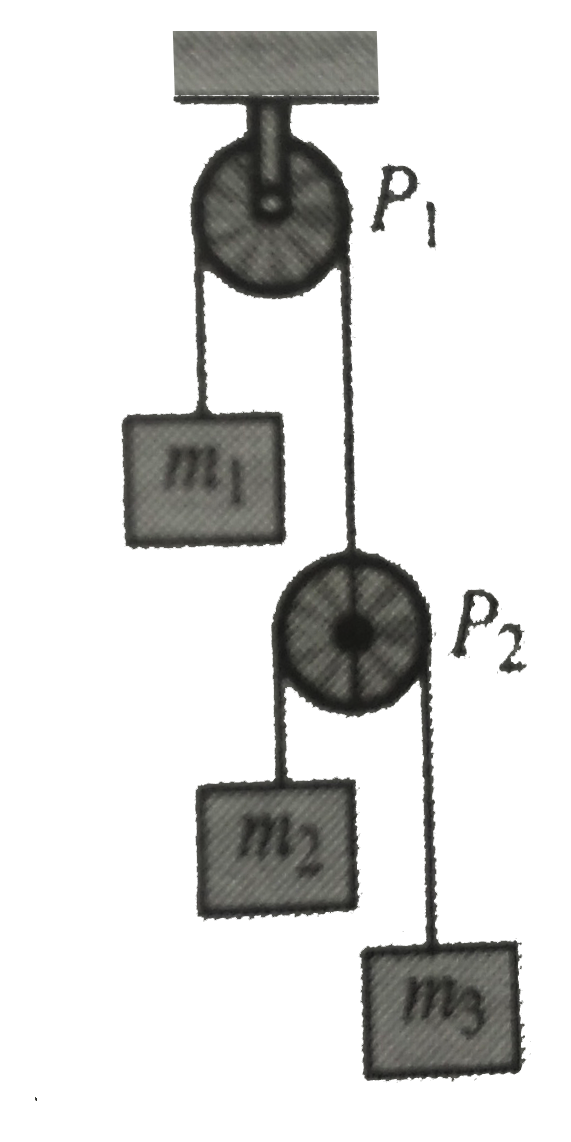
Appling the equations of motion for pulleys and blocks
For $m_{1} : T - m_{1} g = m_{1} a_{1}$ ….(i)
For $m_{2} : m_{2} g - T_{2} = m_{2} a_{2}$ …(ii)
For pulley $P_{1} : 2 T - T = 0 \times a_{p_{1}}$
For pulley $P_{2} : T_{2} - T = 0 \times a_{p_{2}}$ …(iv)

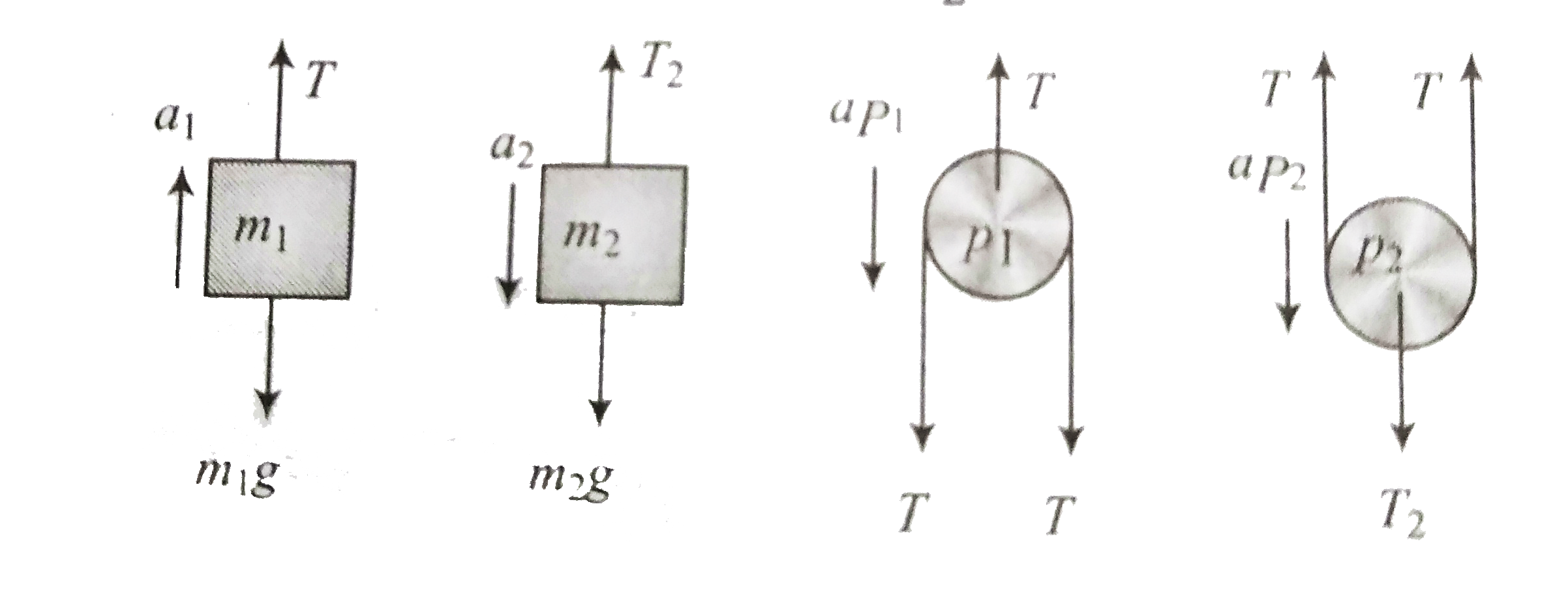
From Eq (iii), $T = 0$ , from (iv), $T_{2} = 0$ and from (i) and (ii). $a_{1} = - g$ , also $a_{2} = g$ . Hence, blocks $m_{1}$ and $m_{2}$ both will move down with acceleration g downward direction.
Calculating $a_{P_{1}}$ and $a_{P_{2}}$
Constraint relations: Consider the reference line and the position vectors of the pulley and masses as shown in fig .write the length of the rope in terms of position vector and differentiate it to obtain the relation between acceleration of the masses and pulleys.

* For the length of the string connecting $P_{2}$ and $m_{2}$ not to change and for this rope not to slacken, $a_{p_{2}} = a_{2} = g$ .
* Length of the string connecting $P_{1}$ to $m_{1}$ not to change and for this rope not to slacken:
$l = (x_{1} - x_{P_{1}}) + x_{P_{1}} + (x_{P_{2}} - x_{P_{1}}) + x_{P_{2}}$
$= x_{1} - x_{P_{1}} + x_{P_{2}}$
Differentiating this equation w.r.t twice we get
$\frac{d^{2} l}{{d t}^{2}} = \frac{d^{2} x_{1}}{{d t}^{2}} - \frac{d^{2} x_{P_{1}}}{{d t}^{2}} + 2 \frac{d^{2} x_{P_{2}}}{{d t}^{2}} \Rightarrow 0 = a_{1} - a_{P_{1}} - 2 a_{P_{2}}$
$\Rightarrow 0 = g - a_{P_{1}} + 2 g \Rightarrow a_{P_{1}} = 3 g$ .

|

Updated on:21/07/2023

Class 11 PHYSICS NEWTONS LAW OF MOTION

Topper's Solved these Questions

Similar Questions

CENGAGE PHYSICS ENGLISH-NEWTON'S LAWS OF MOTION 1-Integer

Home
Ask Doubt
Profile