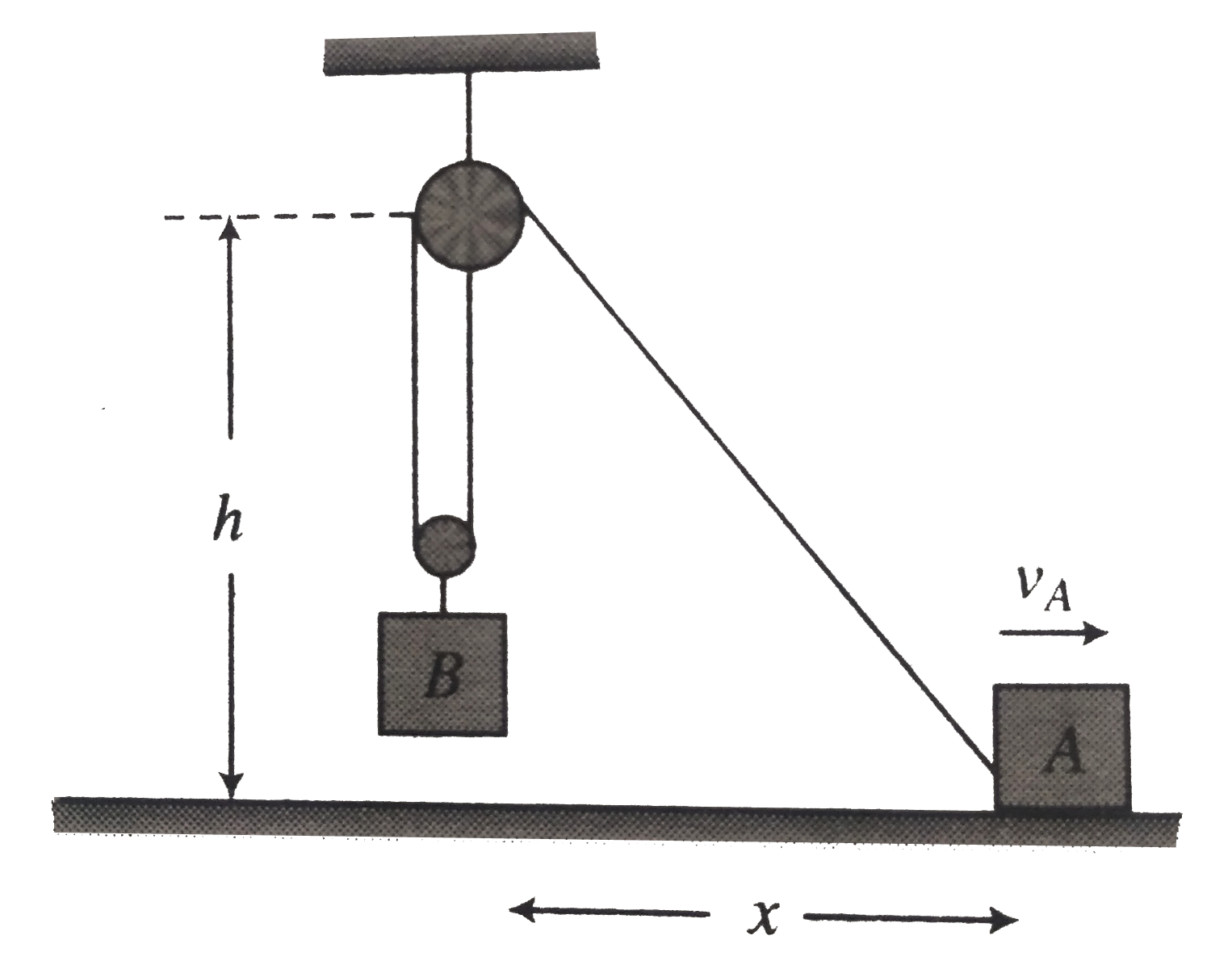
If block A is moving horizontally with velocity vA, then find the velocity of block B at the instant as shown in fig.
hvA2√x2+h2
xvA√x2+h2
xvA2√x2+h2
hvA√x2+h2
The correct Answer is:C
From fig., L=2h−2y+√x2+h2
Differentiating the equation, we get
dydt=x2√h2+x2ddt
⇒VB=xVA2√h2+x2
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Multiple Correct11videos
NEWTON'S LAWS OF MOTION 1
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Assertion-reasoning15videos
NEWTON'S LAWS OF MOTION 1
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Subjective15videos
NEWTON'S LAWS OF MOTION 1
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 2EXERCISE - INTEGER_TYPE10videos
MISCELLANEOUS VOLUME 2
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Integer type1videos
NEWTON'S LAWS OF MOTION 2
Similar Questions
The velocity of the block B is:
 View Solution
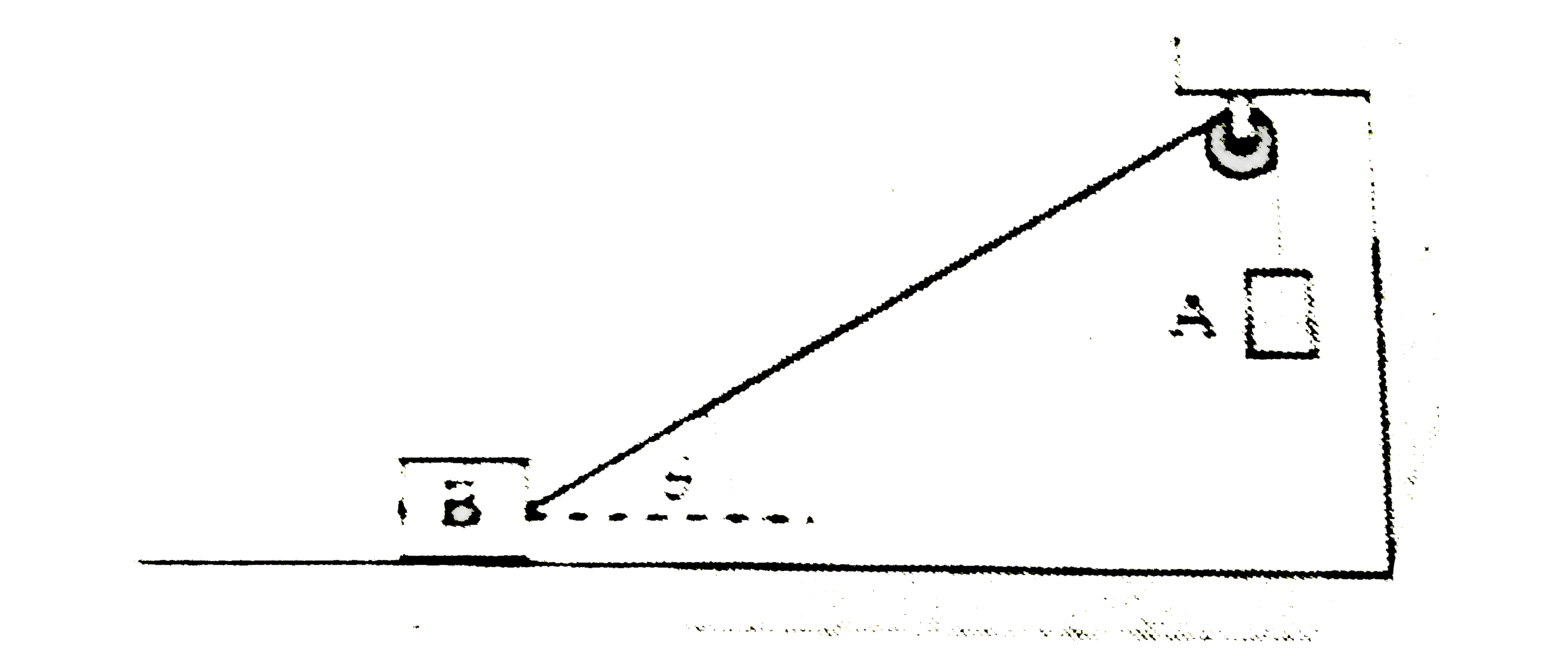
View SolutionThe block A is moving downward with constant velocity v0. Find the velocity of the block B. When the string makes an angle θ with the horizontal
 View Solution
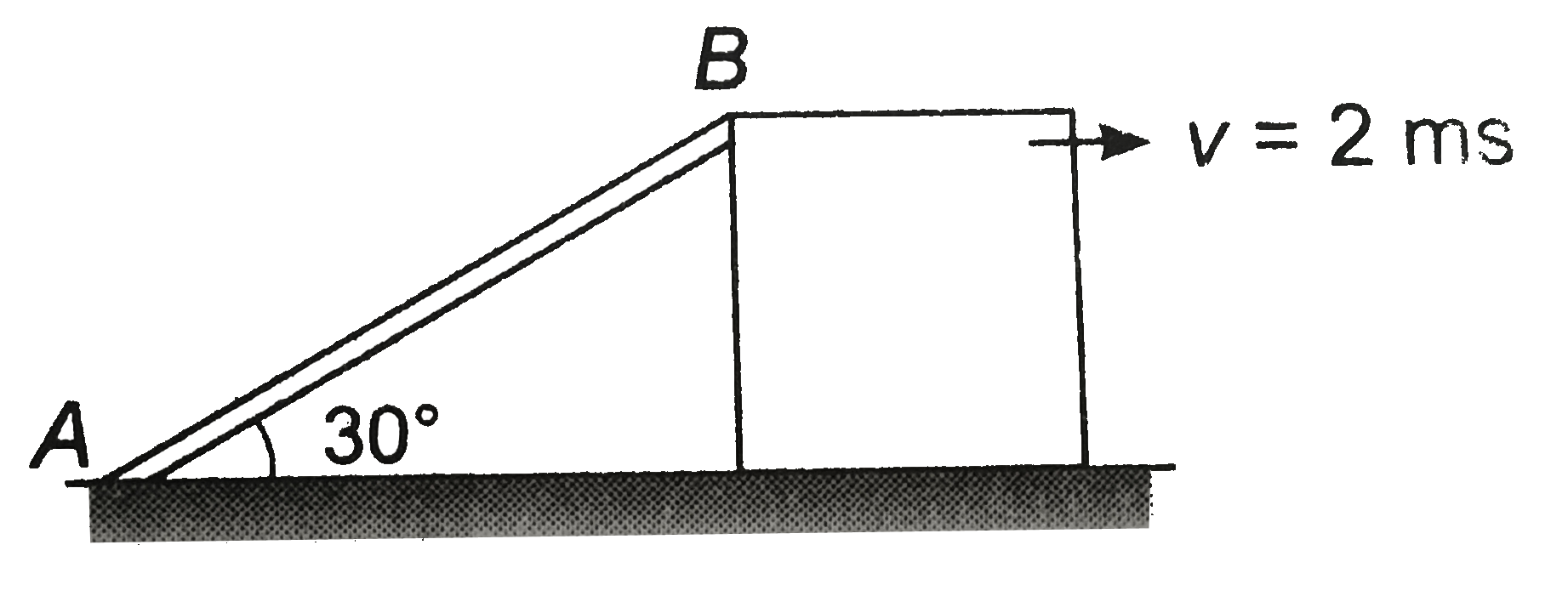
View SolutionA rod AB is shown in figure. End A of the rod is fixed on the ground. Block is moving with velocity 2ms−1 towards right. The velocity of end B of rod at the instant shown in figure is
 View Solution
View SolutionAn inextensible string AB is tied to a block B of negligible dimensions and passes over a small pulley C so that free end A hangs h unit above the ground on which the block B rests. In this initial position shown in fig. The free end A is h unit below C. if now end A moves horizontally with a velocity v0, obtain an expression for the velocity of the block at any time t.
 View Solution
View SolutionA disc of radius R is moving on a rough horizontal surface with velocity v and angular speed ω at an instant as shown in figure. Choose the correct statement.
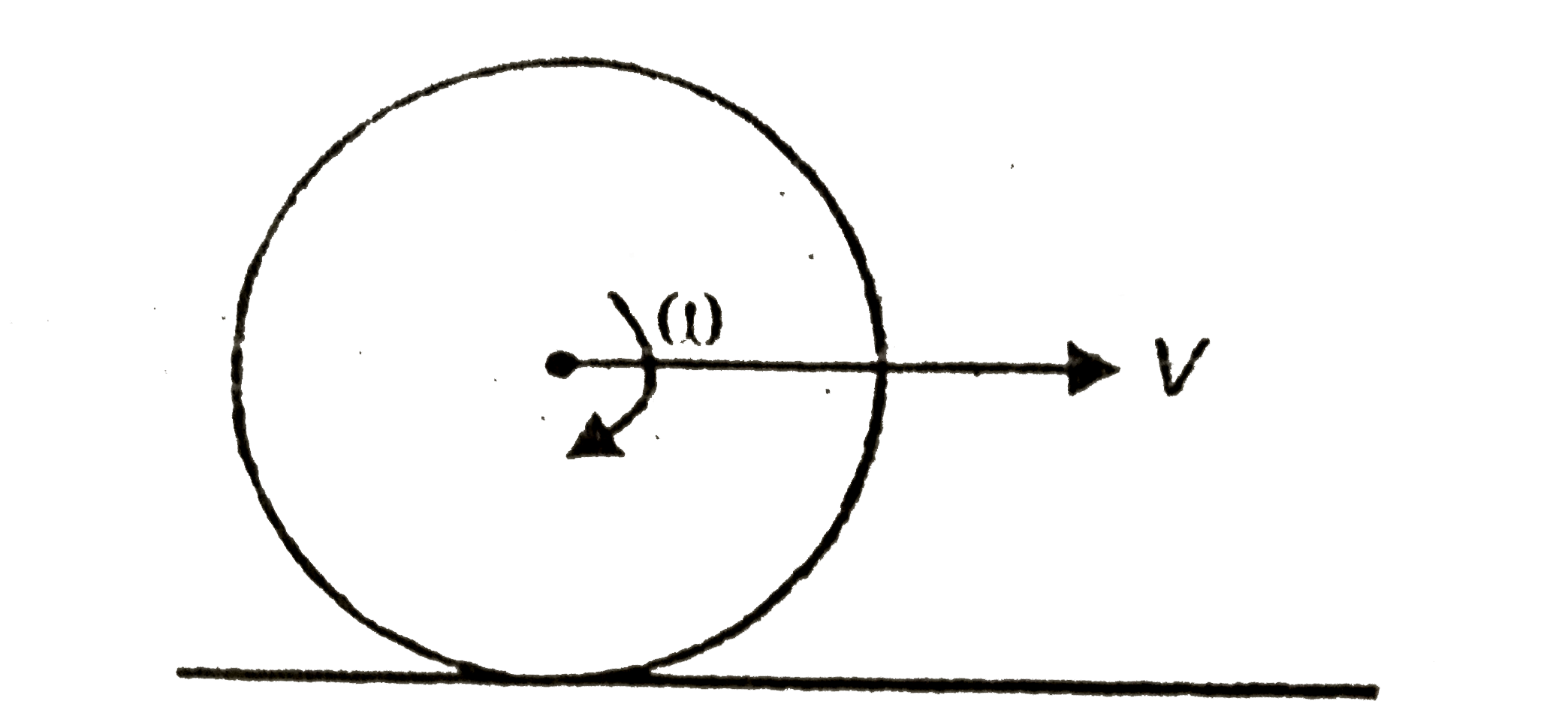 View Solution
View SolutionBlock B moves to the right with a constant velocity v0. The velocity of body a relative to b is
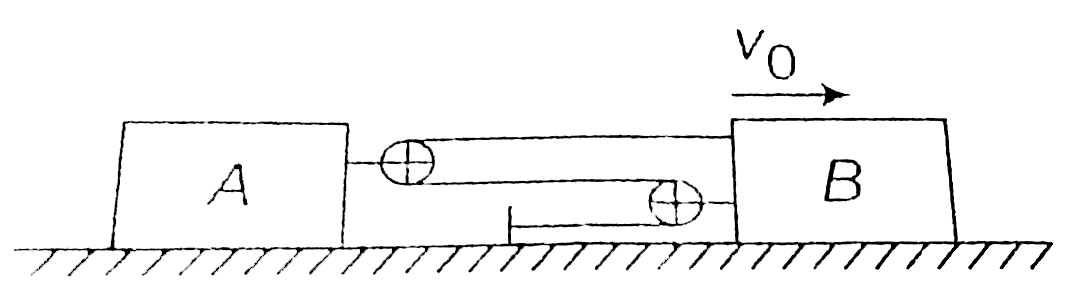 View Solution
View SolutionFind the angular velocity of A with respect to O at the instant shown in (Fig. 5.165).
 .View Solution
.View SolutionThe block shown is moving with constant velocity. Find μk between the block and the surface.
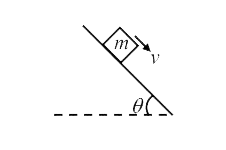 View Solution
View SolutionA block of mass m moving with velocity v0 on a smooth horizontal surface hits the spring of constant k as shown. The maximum compression in spring is
 View Solution
View SolutionIn the system shown, the block A is moving down eith velocity v1 and C is moving up with velocity v3. Express velocity of the block B in terms of velocities of the blocks a and C.
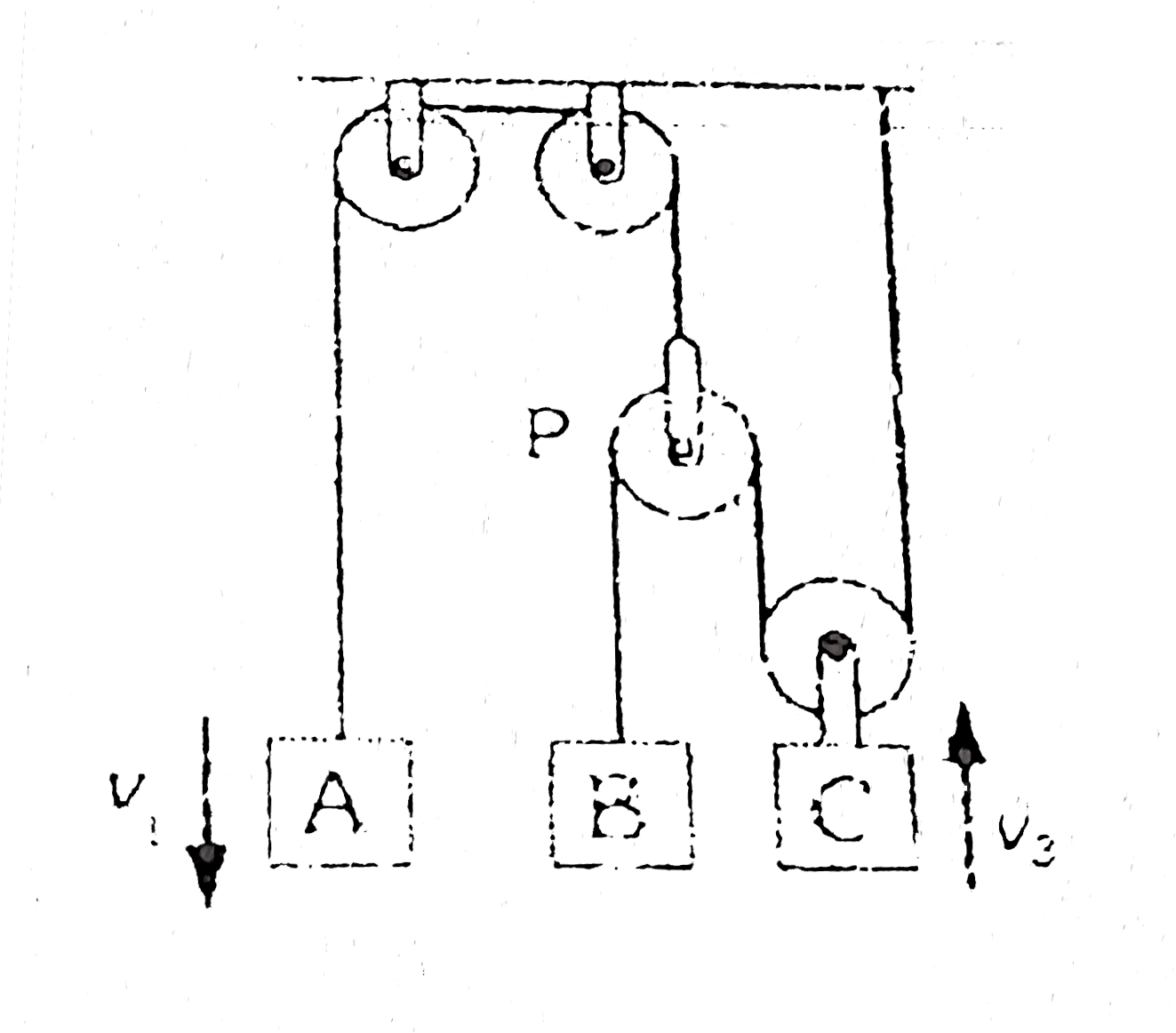 View Solution
View Solution

