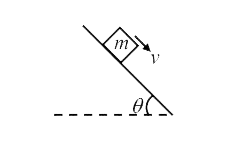
The block shown is moving with constant velocity. Find μk between the block and the surface.
tanθ
cotθ
sinθ
cosθ
The correct Answer is:a
Since the velocity of the block is constant, net force parallel to the incline is zero
→mgsinθ=μkN=μk(mgcosθ)→tanθ=μk
Topper's Solved these Questions
- INTRODUCTION TO VECTORS & FORCES BOOK - VMC MODULES ENGLISHCHAPTER - INTRODUCTION TO VECTORS & FORCES EXERCISE - JEE Main ( ARCHIVE ) ( LEVEL-1)
12 Videos
- INTRODUCTION TO VECTORS & FORCES BOOK - VMC MODULES ENGLISHCHAPTER - INTRODUCTION TO VECTORS & FORCES EXERCISE - JEE Advanced ( ARCHIVE LEVEL-2)
12 Videos
- INTRODUCTION TO VECTORS & FORCES BOOK - VMC MODULES ENGLISHCHAPTER - INTRODUCTION TO VECTORS & FORCES EXERCISE - level 1
75 Videos
- GRAVITATIONBOOK - VMC MODULES ENGLISHCHAPTER - GRAVITATIONEXERCISE - JEE Advance (Archive) TRUE/FALSE
1 Videos
- JEE MAIN - 5BOOK - VMC MODULES ENGLISHCHAPTER - JEE MAIN - 5EXERCISE - PART I : PHYSICS (SECTION - 2)
5 Videos
Similar Questions
In the block moves up with constant velocity v m/s. Find F

View SolutionThe block A is moving downward with constant velocity v0. Find the velocity of the block B. When the string makes an angle θ with the horizontal

View SolutionThe three block shown in fig. move with constant velocities. Find the velocity of blocks A and B. given VP2=10ms−1⏐↓,VC=2ms−1↑⏐.

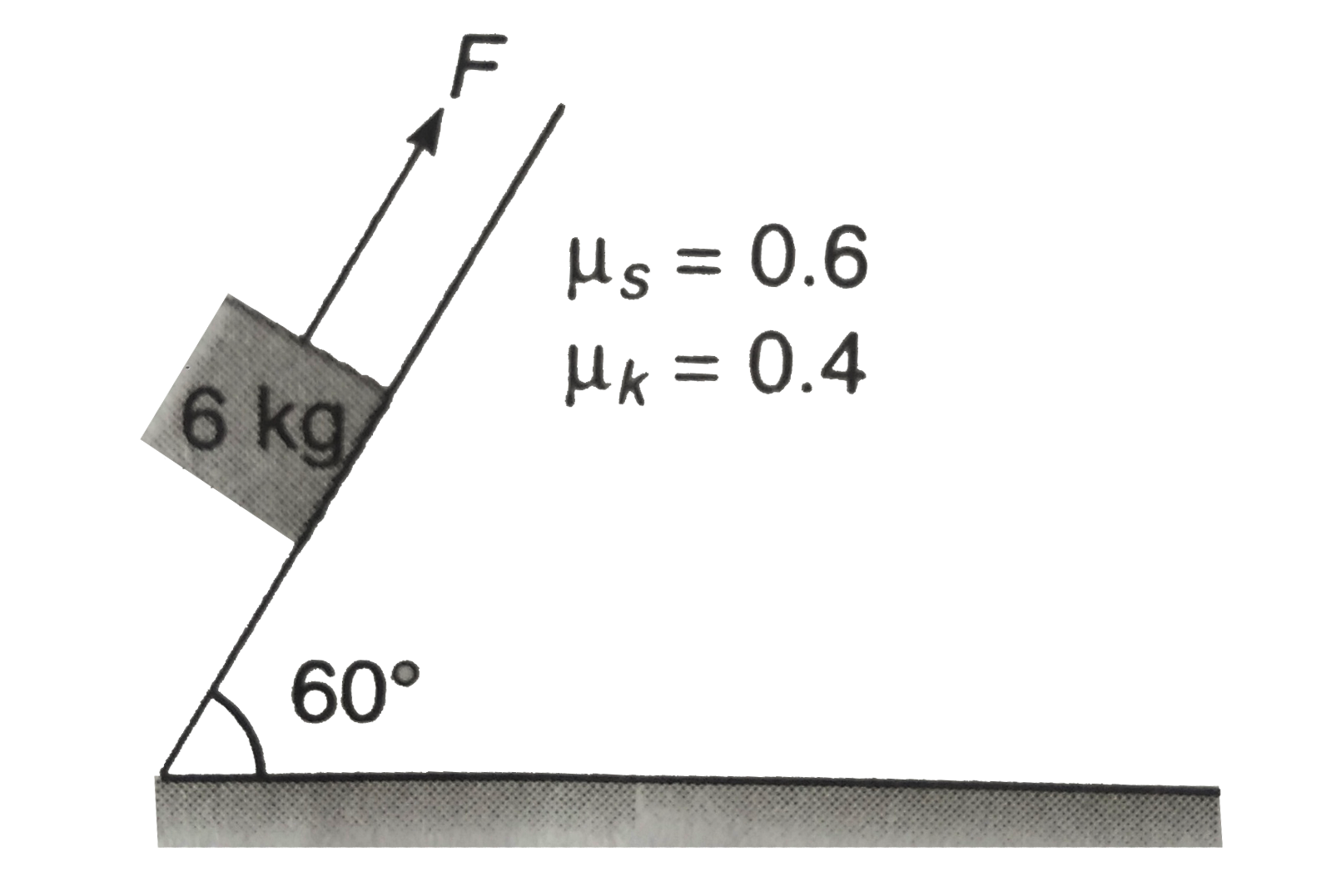
View SolutionA 6kg block is kept on an inclined rough surface as shown in figure.Find the force F requiredto
(a) keep the block stationary.
(b) move the block downwards with contact velocity and
( c) move the block upwards with an acceleration 4m/s2(Takeg=10m/s2)
View SolutionA block of mass m has initial velocity u having direction towards +x axis. The block stops after covering a distnce S causing similar extension in the spring of constant K holding it. If μ is the kinetic friction between the block and the surface on which it was moving, the distance S is given

View SolutionA block of mass m is moving on a rough horizontal surface. μ is the coefficient of kinetic friction between the block and the surface. What is the net force exerted by the surface on the block?
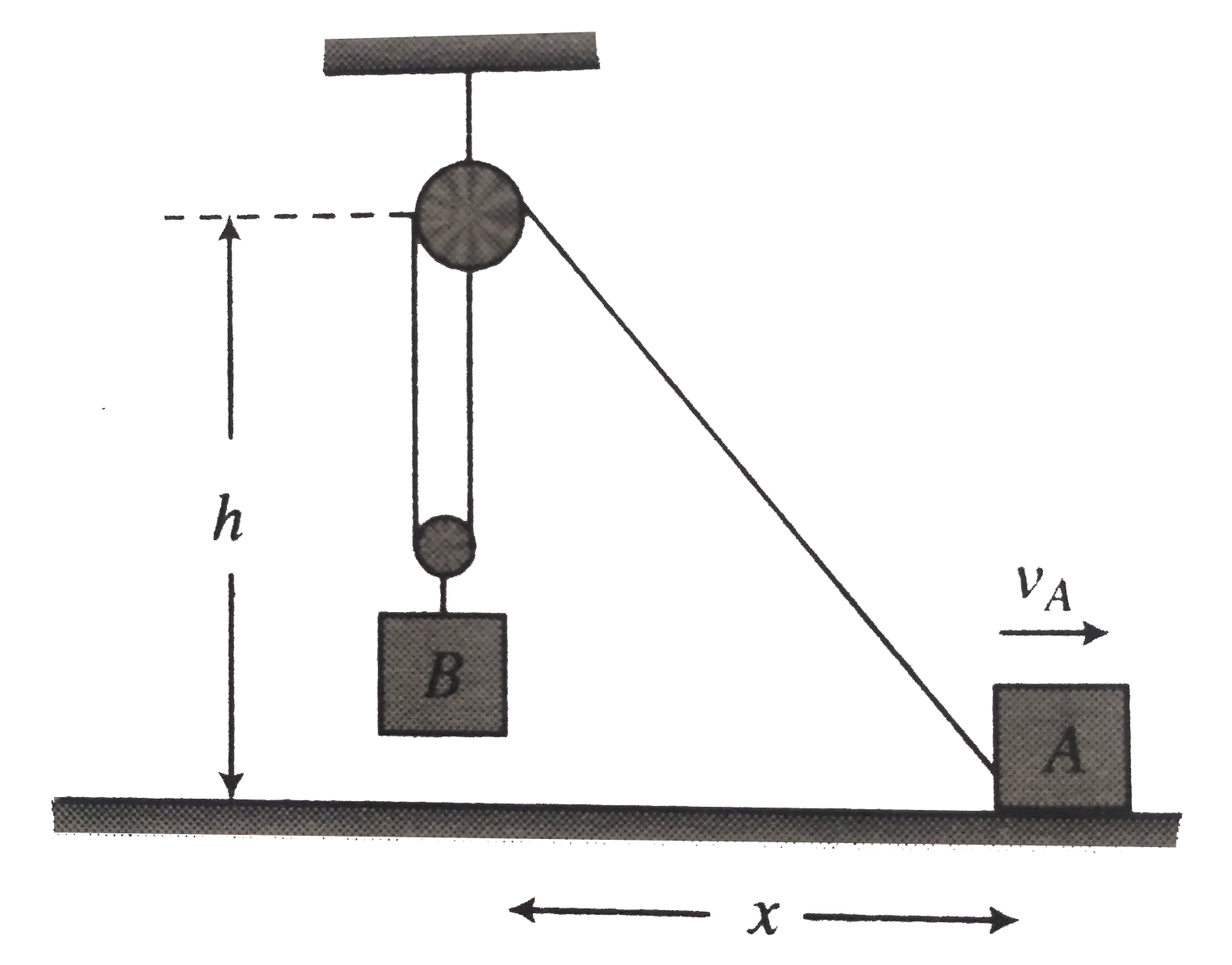
View SolutionIf block A is moving horizontally with velocity vA, then find the velocity of block B at the instant as shown in fig.
View SolutionA block of mass m is pulled by a force of constant power P placed on a rough horizontal plane. The friction coefficient between the block and the surface is μ. Then
View SolutionA block of mass m is attached to one end of a mass less spring of spring constant k. the other end of spring is fixed to a wall the block can move on a horizontal rough surface. The coefficient of friction between the block and the surface is μ then the compession of the spring for which maximum extension of the spring becomes half of maximum compression is .
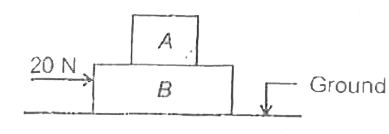
View SolutionBlocks shown in figure moves with constant velocity 20 m/s towards right. All surfaces in contact are rough. The friction force applied by B on A is
View Solution
