A mass of mass 60kg is pulling a mass M by an inextensible light rope passing through a smooth and massless pulley as shown in figure. The coefficient of friction between the mass and ground is μ=1/2 find the maximum value of M that can be pulled on the ground

T=Mg(T= tension in the rope)
N=60g−Tsin60∘(N is normal reaction between the man and the ground) and Tcos60∘=μN
Solving these three equations with proper substitutions, we get
M=120√3+2kg
Topper's Solved these Questions
- NEWTON'S LAWS OF MOTION 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Exercise 7.2
16 Videos
- NEWTON'S LAWS OF MOTION 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Exercise 7.3
27 Videos
- NEWTON'S LAWS OF MOTION 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Solved Examples
12 Videos
- NEWTON'S LAWS OF MOTION 1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Integer
5 Videos
- PROPERTIES OF SOLIDS AND FLUIDSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - INTEGER_TYPE
2 Videos
Similar Questions
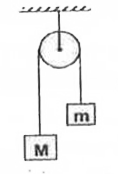
Two masses m and M(m<M) are joined by a light string passing over a smooth and light pulley (as shown)
View SolutionTwo masses of 10 kg and 20 kg are connected with an inextensible string passing over two smooth pulleys as shown in the figure. The acceleration of 20 kg mass will be :
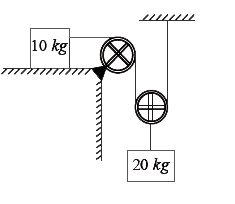
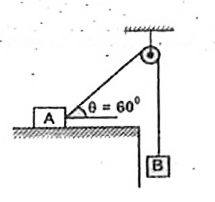
View SolutionTwo blocks A & B are connected by a light inextensible string passing over a fixed smooth pulley as shown in the figure. The coefficient of friction between the block A and the horizontal table is μ=0.2. If the block A is just to slip, find the ratio of the masses of the blocks.
View SolutionA block A of mass m which is placed a rough inclined face of a wedge of same mass being pulled through light string and with force F as shown in figure The coefficient of friction between inclined face and block A is μ while there is no friction between the ground and wedge it the whole system moves with same acceleration then find the value of F

View SolutionA small block of mass 'm' is placed on a plank of mass 'M'. The block is connected to plank with the help of a light string passing over a light smooth pulley as shown in figure. The co-efficient of static friction between the block and plank is μ.
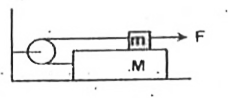
The co-efficient of friction between the plank and the horizontal surface is zero. What maximum horizontal force F applied on the block of mass m can make the block and plank not to slide relatively?
View SolutionA block of mass m is placed on the top of another block of mass M as shown in the figure. The coefficient of friction between them is μ.

The maximum acceleration with which the block M may move so that m also moves along with it is
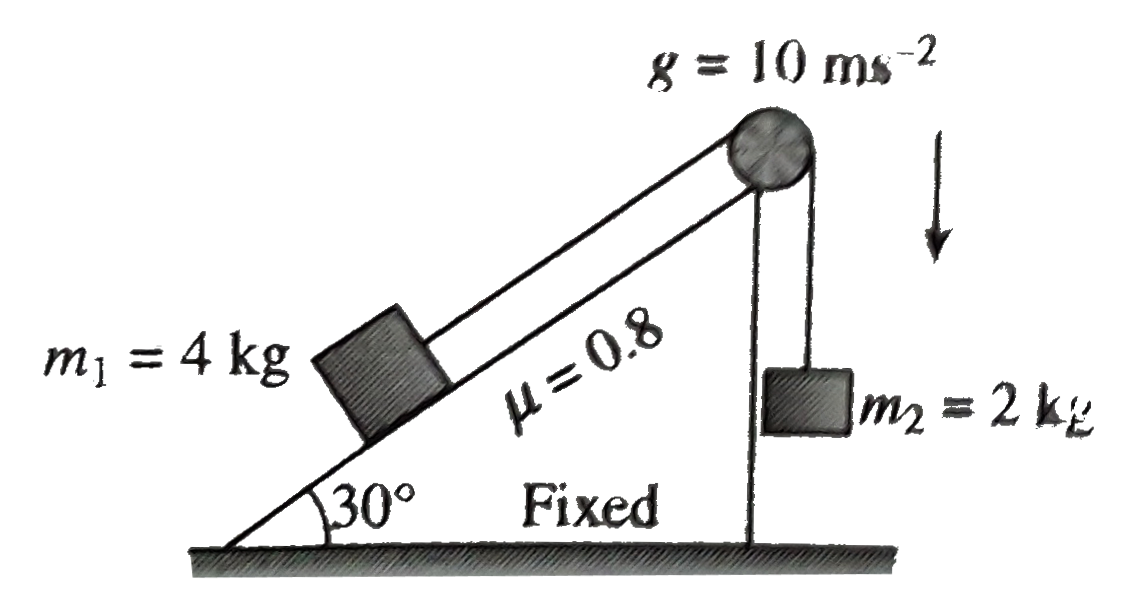
View SolutionTwo blocks of masses m1 and m2 are connected through a massless inextensible string .A block of mass m1 is placed at the fixed rigid inclined surface while the block of mass m2 hanging at the other end of the string which is passing through a fixed massless frictionless pulley shown in figure The coefficient of static friction between the block and the inclined plane is 0.8 The system of masses m1 and m2 released from rest
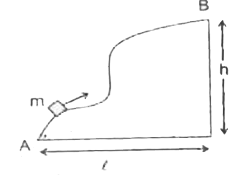
View SolutionA particle of mass m is pulled along an arbitrary curved surface without acceleration as shown in figure. Coefficient of friction between surface and particle is μ. Then

codes:
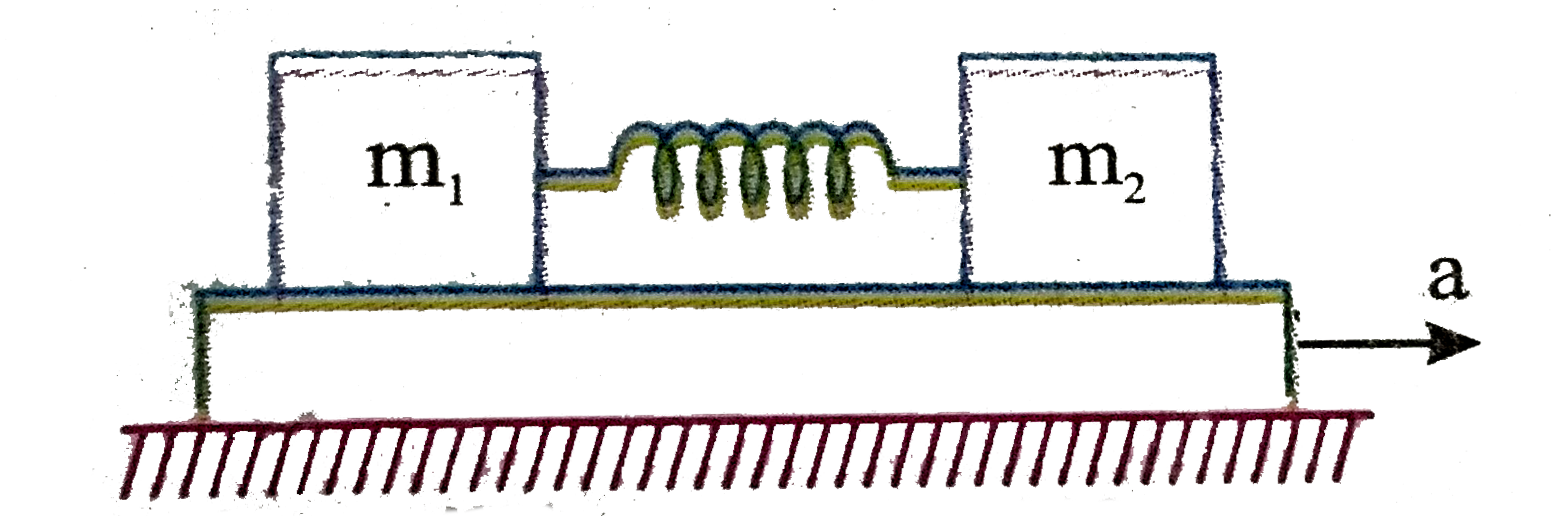
View SolutionTwo block of masses m1 and m2 are connected with a massless unstretched spring and placed over a plank moving with an acceleration 'a' as shown in figure. The coefficient of friction between the blocks and platform is μ
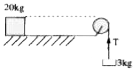
View SolutionA body of mass 20kg is moving on a rough horizontal plane. A block of mass 3kg is connected to the 20 kg mass by a string of negligible mass through a smooth pulley as shown in the figure. The tension in the string is 27 N. The coefficient of kinetic friction between the heavier mass and the surface is (g = 10m/s2)
View Solution