A thin rod of length 1m is fixed in a vertical position inside a train, which is moving horizontally with constant acceleration 4ms−2.A bead can slide on the rod and friction coefficient between them is 0.5. If the bead is released from rest at the top of the rod , it will reach the bottom in
To solve the problem, we will analyze the forces acting on the bead and apply Newton's laws of motion. Here are the steps:
Step 1: Identify the forces acting on the bead
When the bead is released from the top of the rod, it experiences two forces:
1. The gravitational force acting downward: Fg=mg
2. The pseudo force acting horizontally due to the train's acceleration: Fp=ma
Step 2: Determine the normal force
Since the bead is sliding down the rod, the normal force N acting on the bead is equal to the pseudo force:
N=ma
Given that the acceleration a=4m/s2, we can express the normal force as:
N=m⋅4=4m
Step 3: Calculate the limiting friction force
The limiting friction force Ff can be calculated using the coefficient of friction μ:
Ff=μN=μ(ma)=0.5⋅(4m)=2m
Step 4: Analyze the vertical forces
In the vertical direction, the gravitational force mg acts downward while the limiting friction force Ff acts upward. The net force Fnet acting on the bead is:
Fnet=mg−Ff=mg−2m
Substituting g=10m/s2:
Fnet=10m−2m=8m
Step 5: Calculate the acceleration of the bead
Using Newton's second law, the net force is equal to mass times acceleration:
Fnet=ma
Thus,
8m=ma
Dividing both sides by m (assuming m≠0):
a=8m/s2
Step 6: Use the second equation of motion to find the time taken
We can use the second equation of motion to find the time t taken to slide down the rod. The equation is:
s=ut+12at2
Where:
- s=1m (length of the rod)
- u=0 (initial velocity)
- a=8m/s2
Substituting the values:
1=0+12⋅8⋅t2
This simplifies to:
1=4t2
t2=14
t=12s
Final Answer
The bead will reach the bottom of the rod in 0.5 seconds.
---
When the bead is released from the top of the rod, it experiences two forces:
1. The gravitational force acting downward: Fg=mg
2. The pseudo force acting horizontally due to the train's acceleration: Fp=ma
Since the bead is sliding down the rod, the normal force N acting on the bead is equal to the pseudo force:
N=ma
Given that the acceleration a=4m/s2, we can express the normal force as:
N=m⋅4=4m
The limiting friction force Ff can be calculated using the coefficient of friction μ:
Ff=μN=μ(ma)=0.5⋅(4m)=2m
In the vertical direction, the gravitational force mg acts downward while the limiting friction force Ff acts upward. The net force Fnet acting on the bead is:
Fnet=mg−Ff=mg−2m
Substituting g=10m/s2:
Fnet=10m−2m=8m
Using Newton's second law, the net force is equal to mass times acceleration:
Fnet=ma
Thus,
8m=ma
Dividing both sides by m (assuming m≠0):
a=8m/s2
We can use the second equation of motion to find the time t taken to slide down the rod. The equation is:
s=ut+12at2
Where:
- s=1m (length of the rod)
- u=0 (initial velocity)
- a=8m/s2
1=0+12⋅8⋅t2
This simplifies to:
1=4t2
t2=14
t=12s
The bead will reach the bottom of the rod in 0.5 seconds.
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Exercise 7.216videos
NEWTON'S LAWS OF MOTION 2
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Exercise 7.327videos
NEWTON'S LAWS OF MOTION 2
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Solved Examples12videos
NEWTON'S LAWS OF MOTION 2
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Integer5videos
NEWTON'S LAWS OF MOTION 1
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - INTEGER_TYPE2videos
PROPERTIES OF SOLIDS AND FLUIDS
Similar Questions
A block of mass 1kg is horizontal thrown with a velocity of 10ms−1 on a stationary long of mass 2kg whose surface has a μ=0.5. Plane rest on friction surface find the time when m1 comes to rest w.r.t. plane
 03:21View Solution
03:21View SolutionThree masses are atteched to strings rotaing in the horizontal plank .The string pass over two naine as shown in fig will this system be in equilibrium
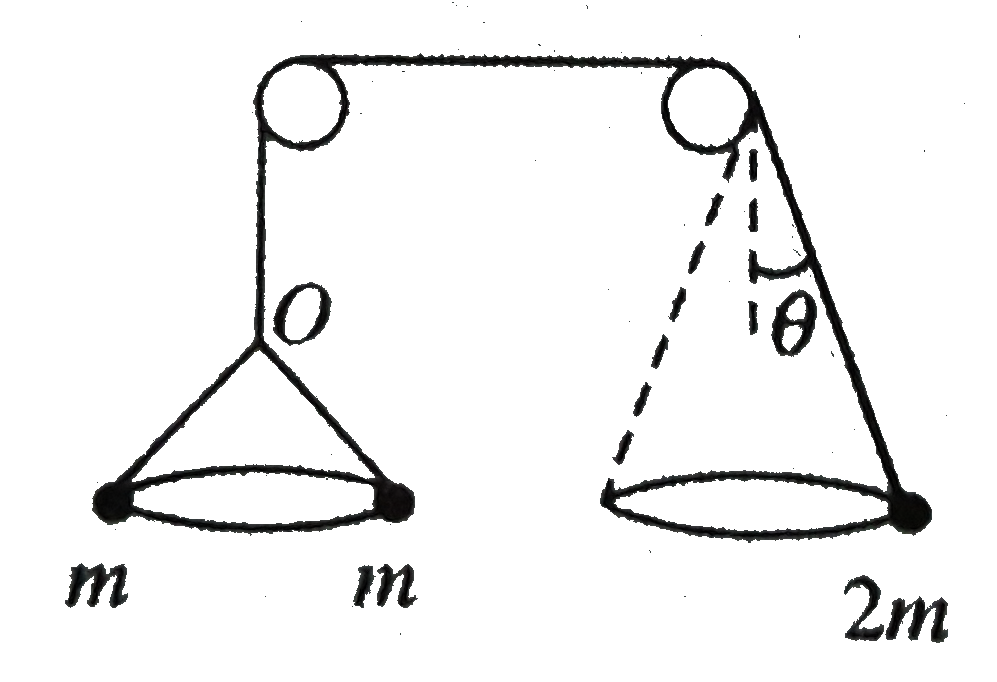 03:22View Solution
03:22View SolutionIn the figure masses m1, m2 and M are 20 kg, 5kg and 50kg respectively. The coefficient of friction between M and ground is zero. The coefficient of friction between m1 and M and that between m2 and ground is 0.3. The pulleys and the strings are massless. The string is perfectly horizontal between P1 and m1 and also between P2 and m2. The string is perfectly vertical between P1 and P2. An external horizontal force F is applied to the mass M. Take g=10m/s2.
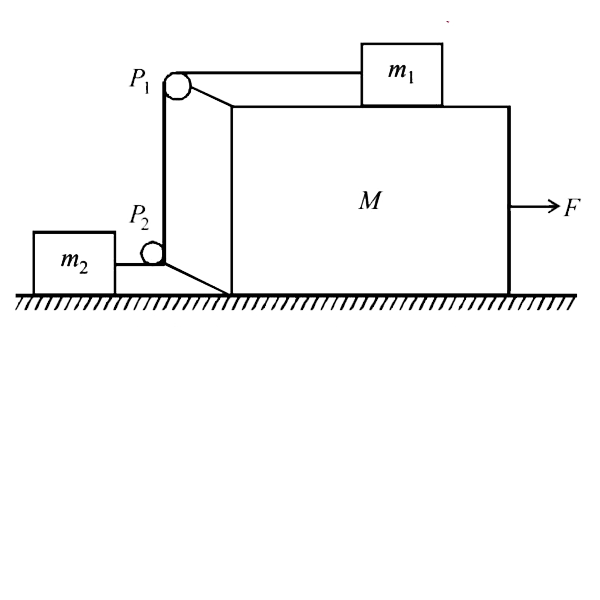
(a) Draw a free body diagram for mass M, clearly showing all the forces.
(b) Let the magnitude of the force of friction between m1 and M be f1 and that between m2 and ground be f2. For a particular F it is found that f1=2f2. Find f1 and f2. Write equations of motion of all the masses. Find F, tension in the spring and acceleration of masses.View SolutionA block is placed on an inclined plane moving towards right horizontally with an acceleration a0=g. The length of the plane AC=1m. Friction is absent everywhere. Find the time taken (in seconds) by the block to reach from C to A.
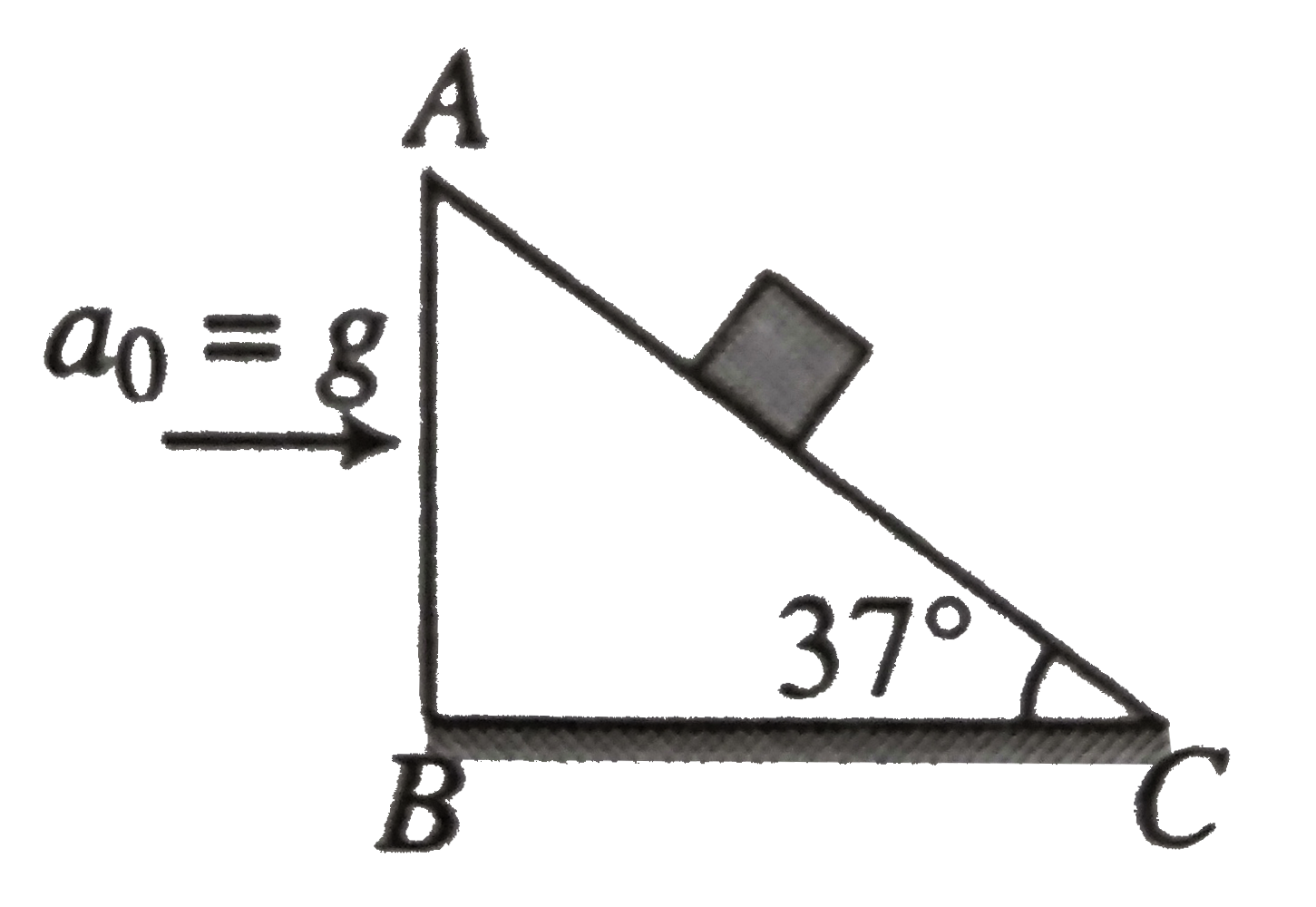 03:23View Solution
03:23View SolutionTwo soap bubbles A and B are kept in aclosed chamber where the air is maintained at pressure 8Nm2. The radiiof bubbles A and B are 2cm and 4 cm , respectively. Surface tension of the soap-water used to make bubbles is 0.04 N/m. The ratio of nB/nAis ( where nA and nB are the numbe of moles of air in bubbles A and B,respectively.)
[Neglect the effect of gravity]05:52View SolutionA thin rod of length 1 m is fixed in a vertical position inside a train, which is moving horizentally with constant acceleration 4 ms^(-2) .A bead can slide on the rod and friction coefficient between them is 0.5 . If the head is released from rest at the top of the rod , it will reach the bottom the in
06:34View SolutionA rod can rotate in a horizontal plane about its one end. A bead which can move along the rod is placed at certain distance from the axis or rotation. The bead does not to friction. The rod has a constant angular acceleration
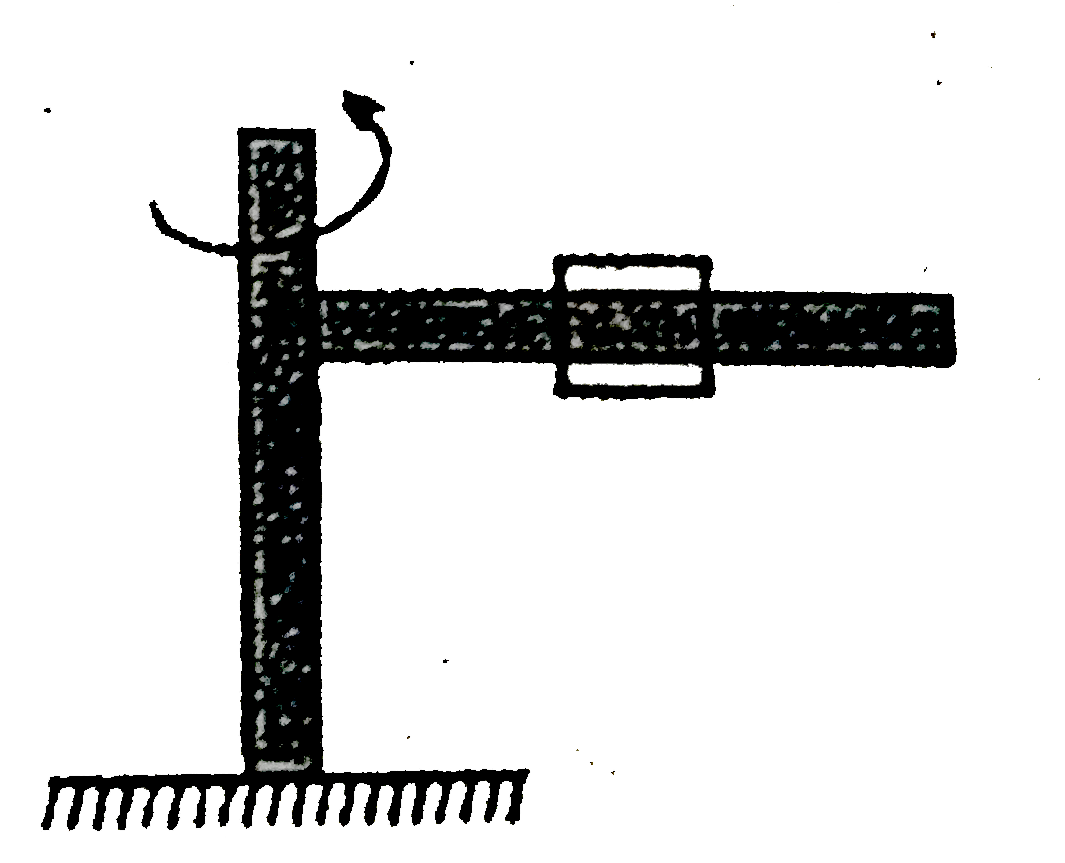 03:38View Solution
03:38View SolutionA uniform rod of mass M and length L is hinged at its lower end so as to rotate freely in the vertical plane of the fig. There is a small tight fitting the hinged end. A small mass less pin welded to the rod supports the bead. The system is released from the vertical position shown. It was observed that the bead just begins to slide on the rod when the rod becomes horizontal.
(a) Find the normal contact force between the rod and the bead when the rod gets horizontal. What is the direction of this force?
(b) Find the coefficient of friction between the bead and rod.
 06:08View Solution
06:08View SolutionA bead of mass m is fitted on a rod and can move on it without friction. Initially the bead is at the middle of the rod moves transitionally in the vertical plane with an accleration a0 in direction forming angle α with the rod as shown. The acceleration of bead with respect to rod is:
z06:08View SolutionA long horizontal rod has a bead which can slide along its length and initially placed at a

distance L from one end A of the rod. The rod is set in angular motion about A with constant angular acceleration α. if the coefficient of friction between the rod and the bead is μ, and gravity is neglected, then the time after which the bead starts slipping is04:50View SolutionA long horizontal rod has a bead which can slide along its length, and initially placed at a distance L from one end A of the rod. The rod is set in angular motion about A with constant angular acceleration a. If the coefficient of friction between the rod and the bead is u, and gravity is neglected, then the time after which the bead starts slipping is :
02:57View SolutionA bead of mass m moves on a rod without friction. Initially the bead is at the middle of the rod and the rod moves translationally in a vertical plane with an acceleration a0 in a direction forming angle θ with the horizontal as shown in the given figure. The acceleration of bead with respect to rod is
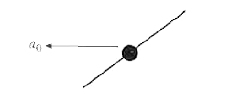 04:11View Solution
04:11View Solutionएक लम्बी क्षैतिज छड़ पर एक मोती पिरोया गया है, यह छड़ कि लम्बाई के अनुदिश फिसल सकता है और प्रारम्भ में यह छड़ के एक सिरे A से L दुरी पर है । छड़ को A के पारित नियत कोणीय त्वरण α से घुमाया जाता है । यदि छड़ एवं मोती के बीच घर्षण गुणांक μ है और गुरुत्व को नगण्य माना जाये तो कितने समय पश्चात मोती फिसलना प्रारम्भ कर देगा ?
03:12View Solutionएक लम्बी क्षैतिज छड़ पर एक मोती पिरोया गया है, यह छड़ कि लम्बाई के अनुदिश फिसल सकता है और प्रारम्भ में यह छड़ के एक सिरे A से L दुरी पर है । छड़ को A के पारित नियत कोणीय त्वरण α से घुमाया जाता है । यदि छड़ एवं मोती के बीच घर्षण गुणांक μ है और गुरुत्व को नगण्य माना जाये तो कितने समय पश्चात मोती फिसलना प्रारम्भ कर देगा ?
05:53View SolutionA long horizontal rod has a bead which can slide along its length and initially placed at a

distance L from one end A of the rod. The rod is set in angular motion about A with constant angular acceleration α. if the coefficient of friction between the rod and the bead is μ, and gravity is neglected, then the time after which the bead starts slipping is04:15View Solution

