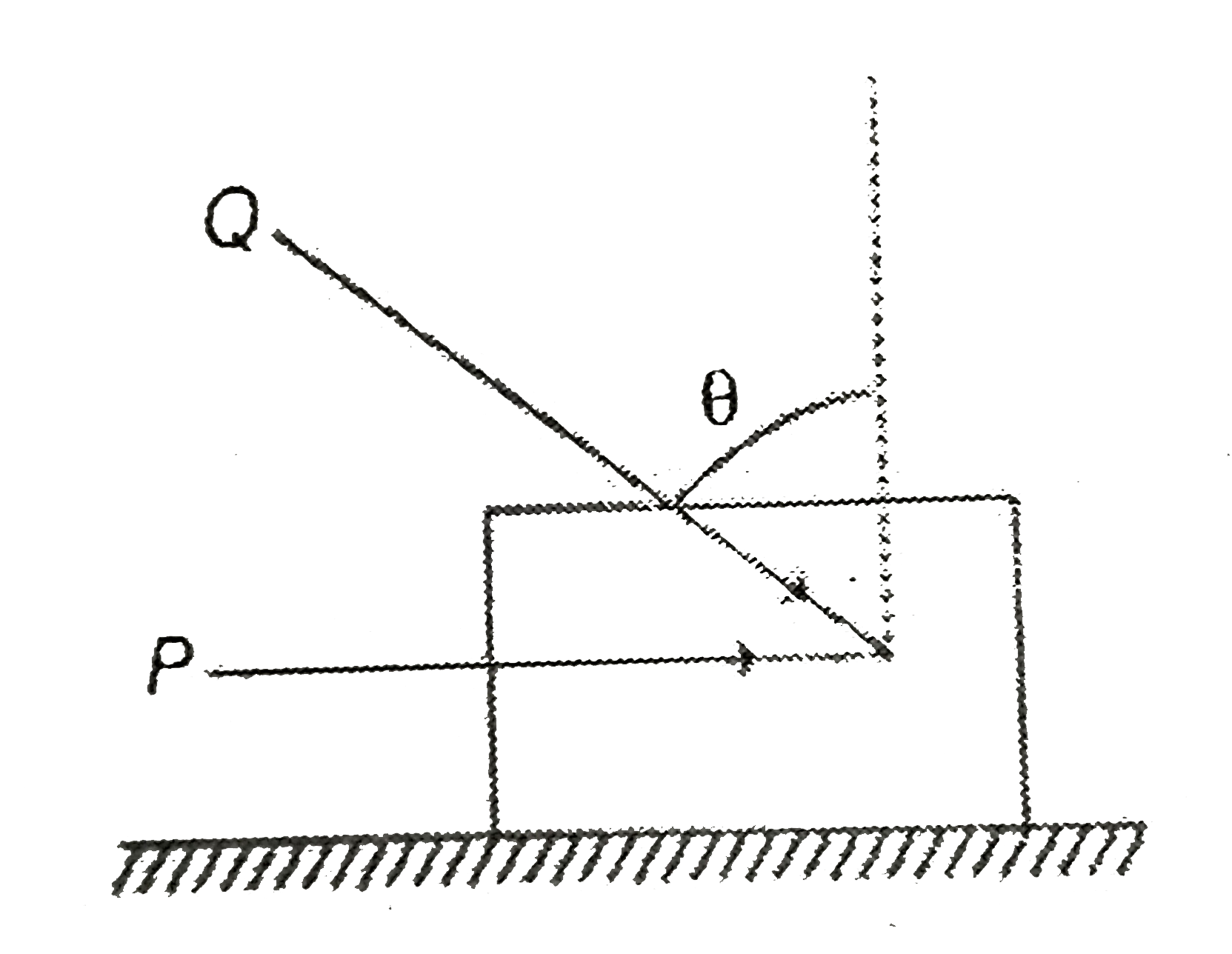
A block of mass m lying on a rough horizontal plane is acted upon by a horizontal force P and another force Q inclined at an angle θ to the vertical. The minimum value of coefficient of friction of friction between the block and the surface for which the block will remain in equilibrium is
(Psinθ−Q)/(mg−cosθ)
(P−Qsinθ)/(mg+cosθ)
(Pcosθ+Q)/(mg−cosθ)
(P+Qsinθ)/(mg+Qcosθ)
The correct Answer is:b
Frictional force=μR=μ(mg+Qcosθ) and horizontal push =P−Qsinθ
For equilibrium we have
μ(mg+Qcosθ)=P−Qsinθ⇒μ=P−Qsinθmg+Qcosθ
Topper's Solved these Questions
- NEWTON'S LAWS OF MOTION 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Multiple Correct
2 Videos
- NEWTON'S LAWS OF MOTION 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Linked Comprehension
52 Videos
- NEWTON'S LAWS OF MOTION 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Subjective
21 Videos
- NEWTON'S LAWS OF MOTION 1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Integer
5 Videos
- PROPERTIES OF SOLIDS AND FLUIDSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - INTEGER_TYPE
2 Videos
Similar Questions
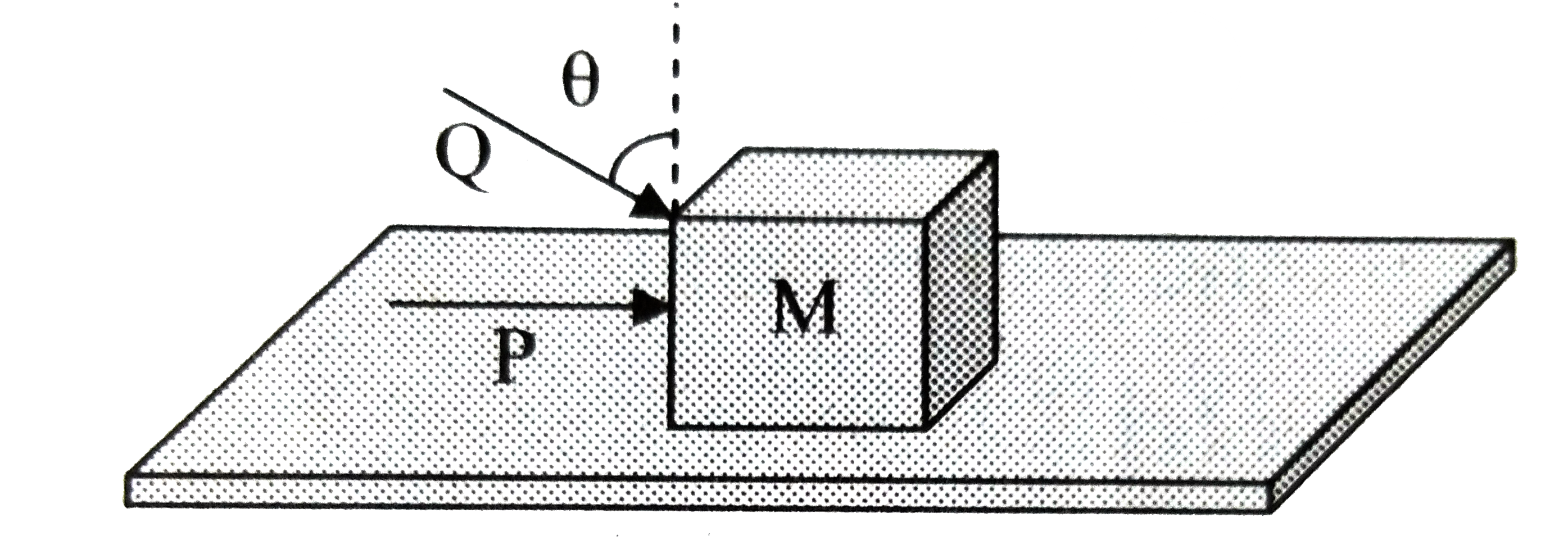
A block of mass m lying on a rough horizontal plance is acted upon by a horizontal force P and another force Q inclined at an angle θ to the vertical. The block will remain in equilibrium, if the coefficient of friction between it and the surface is
View Solution
A wedge of mass m, lying on a rough horizontal plane, is acted upon by a horizontal force F1 and another force F2, inclined at an angle θ to the vertical. The block is in equilibrium, then minimum coefficient of friction between it and te surface is
View Solution
Knowledge Check
A block of mass 2kg rests on a rough inclined plane making an angle of 30∘ with the horizontal. The coefficient of static friction between the block and the plane is 0.7. The frictional force on the block is
A10.3NB23.8NC11.9ND6.3N
A block of mass 4kg rests on a rough horizontal plane. The plane is gradually inclined until at an angle θ=60∘ , with the vertical, the mass just begins to side. What is the coefficient of static friction between the block and the plane?
View SolutionA wooden block of mass M resting on a rough horizontal surface is pulled with a force T at an angle q to the horizontal. If m is coefficient of kinetic friction between the block and the surface, the acceleration of the block is
View SolutionA block of weight 200N is pulled along a rough horizontal surface at constant speed by a force 100N acting at an angle 30∘ above the horizontal. The coefficient of friction between the block and the surface is
View SolutionA block of mass m slides down an inclined plane which makes an angle θ with the horizontal. The coefficient of friction between the block and the plane is μ. The force exerted by the block on the plane is
View SolutionA block of mass m is placed at rest on a horizontal rough surface with angle of friction ϕ. The block is pulled with a force F at an angle θ with the horizontal. The minimum value of F required to move the block is
View SolutionA block of mass m is placed at rest on a horizontal rough surface with angle of friction ϕ. The block is pulled with a force F at an angle θ with the horizontal. The minimum value of F required to move the block is
View SolutionA block of mass 2kg rests on a rough inclined plane making an angle of 30∘ with the horizontal. The coefficient of static friction between the block and the plane is 0.7. The frictional force on the block is
View Solution
