A ball of mass m is thrown in air with speed from a height and it is at a height when its speed becomes . Find the work done on the ball the air resistance.
To find the work done on the ball by air resistance, we can use the work-energy theorem, which states that the total work done on an object is equal to the change in its kinetic energy.
Let's break down the solution step by step:
Step 1: Understand the Problem
We have a ball of mass m thrown upwards from a height h1 with an initial speed v1. It reaches a height h2 with a speed v2. We need to find the work done by air resistance during this motion.
Step 2: Apply the Work-Energy Theorem
According to the work-energy theorem:
Wtotal=ΔKE
Where Wtotal is the total work done on the ball, and ΔKE is the change in kinetic energy.
Step 3: Calculate Change in Kinetic Energy
The change in kinetic energy (ΔKE) can be calculated as:
ΔKE=KEf−KEi=12mv22−12mv21
This simplifies to:
ΔKE=12m(v22−v21)
Step 4: Calculate Work Done by Gravity
The work done by gravity (Wg) when the ball moves from height h1 to height h2 is given by:
Wg=−mg(h2−h1)
The negative sign indicates that gravity does work against the upward motion of the ball.
Step 5: Relate Work Done by Air Resistance
The total work done on the ball can be expressed as:
Wtotal=Wg+Wair
Where Wair is the work done by air resistance. Rearranging gives:
Wair=Wtotal−Wg
Step 6: Substitute the Values
Substituting the expressions for Wtotal and Wg:
Wair=ΔKE−(−mg(h2−h1))
Wair=12m(v22−v21)+mg(h2−h1)
Final Expression
Thus, the work done by air resistance is:
Wair=12m(v22−v21)+mg(h2−h1)
We have a ball of mass m thrown upwards from a height h1 with an initial speed v1. It reaches a height h2 with a speed v2. We need to find the work done by air resistance during this motion.
According to the work-energy theorem:
Wtotal=ΔKE
Where Wtotal is the total work done on the ball, and ΔKE is the change in kinetic energy.
The change in kinetic energy (ΔKE) can be calculated as:
ΔKE=KEf−KEi=12mv22−12mv21
This simplifies to:
ΔKE=12m(v22−v21)
The work done by gravity (Wg) when the ball moves from height h1 to height h2 is given by:
Wg=−mg(h2−h1)
The negative sign indicates that gravity does work against the upward motion of the ball.
The total work done on the ball can be expressed as:
Wtotal=Wg+Wair
Where Wair is the work done by air resistance. Rearranging gives:
Wair=Wtotal−Wg
Substituting the expressions for Wtotal and Wg:
Wair=ΔKE−(−mg(h2−h1))
Wair=12m(v22−v21)+mg(h2−h1)
Thus, the work done by air resistance is:
Wair=12m(v22−v21)+mg(h2−h1)
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WORK, POWER & ENERGYEXERCISE - Exercise 8.326videos
WORK, POWER & ENERGY
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WORK, POWER & ENERGYEXERCISE - Exercise 8.416videos
WORK, POWER & ENERGY
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WORK, POWER & ENERGYEXERCISE - Exercise 8.125videos
WORK, POWER & ENERGY
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - VECTORSEXERCISE - Exercise Multiple Correct5videos
VECTORS
Similar Questions
A ball is thrown upwards with a speed u from a height h above the ground.The time taken by the ball to hit the ground is
View SolutionA small ball of mass m is thrown upward with velocity u from the ground. The ball experiences a resistive force mkv2 where v is its speed. The maximum height attained by the ball is :
View Solution
Knowledge Check
- Question 1 - Select One
A ball of mass m collides with a wall with speed v and rebounds on the same line with the same speed. If the mass of the wall is taken as infinite, then the work done by the ball on the wall is
Amv2B12mv2C2mvDzero - Question 2 - Select One
A ball of mass m is thrown vertically up with an initial velocity so as to reach a height h.The correct statement is :
APotential energy of the ball at the ground is mgh.BKinetic energy of the ball at ground is zeroCKinetic energy of the ball at the highest point is mgh .DPotential enengy of the ball at the highest point is mgh.
A baseball of mass m is thrown upward with some initial speed. If air resistance is neglected, what is the force on the ball: (a) when it reaches half its maximum height, and (b) when it reaches its peak?
View SolutionA ball of mass 'm' is thrown with a speed v0 towards a bat. It rebounds along the same speed 2v0 . The variation of interaction force between the bat and ball is shown
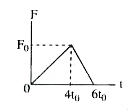
Average force exerted by the bat on the ball isView SolutionA ball of mass 'm' is thrown with a speed v0 towards a bat. It rebounds along the same speed 2v0 . The variation of interaction force between the bat and ball is shown
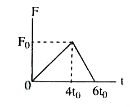
Maximum force exerted by the bat on the ball isView SolutionA body of mass 'm is drhopped from a height 'h'. The speed with which body hits the ground is √0.9gh Find the work done by air-resistance furing its fall.
View SolutionA ball of mass m moves with speed v and stricks a wall having infinite mass and it returns with same speed then the work done by the ball on the wall is
View SolutionTwo balls of different masses are thrown vertically upwards with the same speed . They pass through the point of projection in their downward motion with the same speed ( Neglect air resistance ).
View Solution

