A spring block system is placed on a rough horizontal surface having coefficient of friciton μ. The spring is given initial elongation 3μmg/k (where m=mass of block and k=spring constant) and the block is released from rest. For the subsequent motion, find
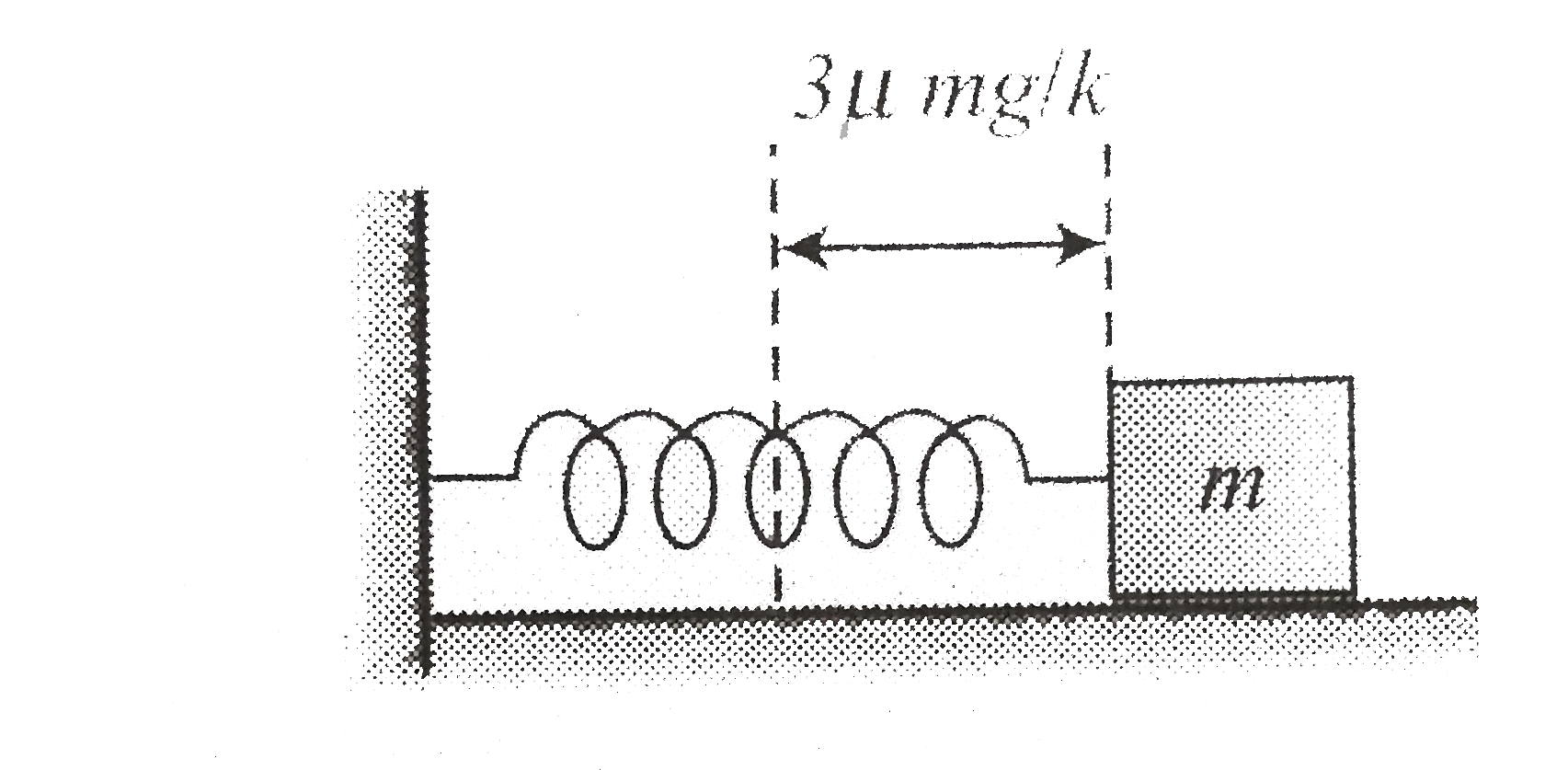
a. Initial acceleration of block
b. Maximum compression in spring
c. Maximum speed of the block
a. From Newton's second law, we get
ma=3μmg−μmg⇒a=2μg
b. From work energy principle
Wspr∈g+Wspr∈g=0
12k(x20−x21)−μmg(x1+x0)=0
x0−x1=2μmgk⇒x1=μmgk
c. Speed will be maximum where net force is zero
μmg=kx
⇒x=μmgk (extension)
Now from work-energy principle, we have
12k(μmgk)2(32−12)−2μmgk(μmg)=12mv2
Solving we get, v=2μg√mk
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WORK, POWER & ENERGYEXERCISE - Exercise 8.326videos
WORK, POWER & ENERGY
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WORK, POWER & ENERGYEXERCISE - Exercise 8.416videos
WORK, POWER & ENERGY
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WORK, POWER & ENERGYEXERCISE - Exercise 8.125videos
WORK, POWER & ENERGY
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - VECTORSEXERCISE - Exercise Multiple Correct5videos
VECTORS
Similar Questions
Find the maximum tension in the spring if initially spring at its natural length when block is released from rest.
 View Solution
View SolutionA block of mass m is relesed from rest from a height h onto a smooth surface of mass M fitted with an ideal spring of stiffness k. find the maximum compression in the spring.
 View Solution
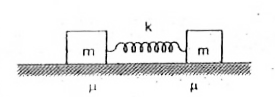
View SolutionTwo blocks each having mass m is attached to each other with a spring having force constant k. The system is placed on a rough horizontal surface having coefficient of friction μ. The maximum initial compression, that can be given to the spring so that when released the blocks do not move is
 View Solution
View SolutionA block of mass m is attached with a spring in vertical plane as shown in the figure. If initially spring is in its natural length and the block is released from rest, then maximum extension in the spring will be
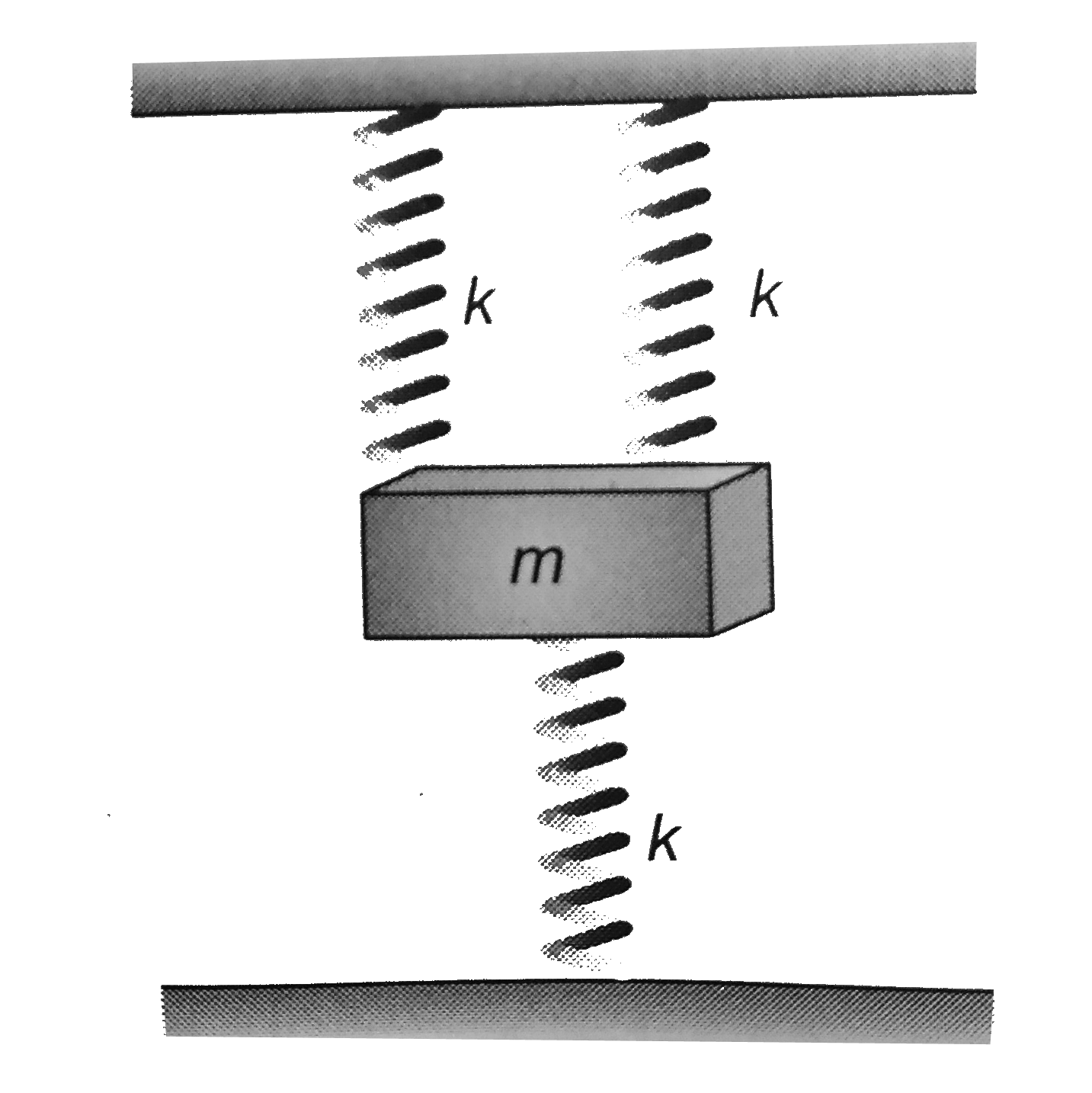
View SolutionIn the figure all spring are identical having spring constant k and mass m each The block also mass m The frequency of oscillation of the block is
 View Solution
View SolutionThe block of mass m is released when the spring was in its natrual length. Spring constant is k. Find the maximum elongation of the spring.
 View Solution
View SolutionIn the adjoining figure, block A is of mass (m) and block B is of mass 2m. The spring has force constant k. All the surfaces are smooth and the system is released form rest with spring unstretched. Find the maximum extension in the spring and acceleration of block B at time of maximum extension
 .View Solution
.View SolutionA block of mass m is attached to a spring of force constant k whose other end is fixed to a horizontal surface. Initially the spring is in its natural length and the block is released from rest. The average force acting on the surface by the spring till the instant when the block has zero acceleration for the first time is
 View Solution
View SolutionA block of mass m moving with velocity v0 on a smooth horizontal surface hits the spring of constant k as shown. The maximum compression in spring is
 View Solution
View SolutionA block of mass m starts at rest at height on a frictionless inclined plane. The block slides down the plane, travels across a rough horizontal surface with coefficient of kinetic friction μ and compresses a spring with force constant k a distance x before momentarilly coming to rest. Then the spring extends and the block travels back across the rough surface, sliding up the plane. The block travels a total distance d on rough horizontal surface. The correct experssion for the maximum height h' that the block reaches on its return is :
 View Solution
View Solution

