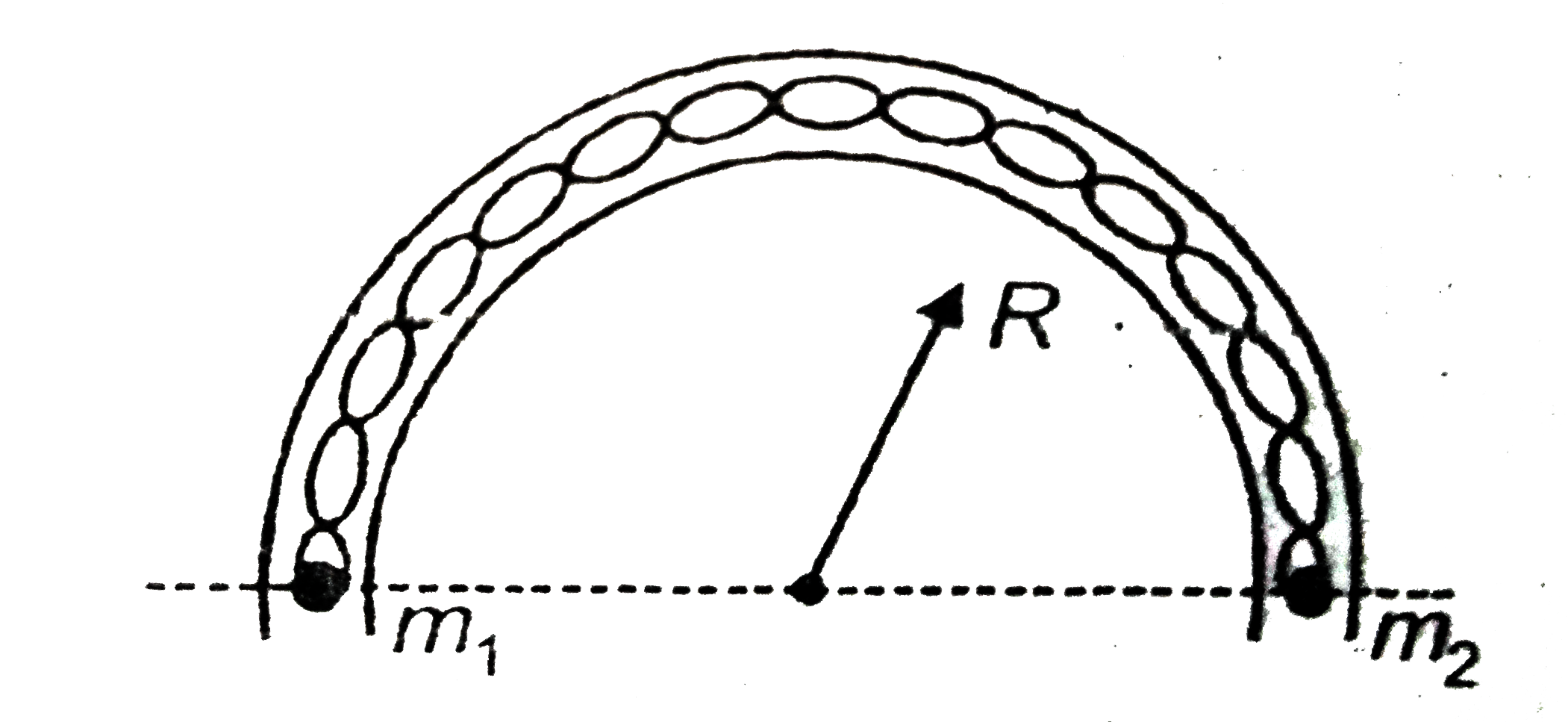
Two smooth balls of mass m1 and m2 connected by a light inextensible string are at the opposite points of horizontal diameter of a smooth semi cylindrical surface of radius R. If m1 is released, find its speed at any angular distance θ moved by m2.

Let the ball m2 moves through an angle θ. The mass m will fall through a distance h1=Rθ.
The ball m2 rises through a height h2 as,
h2=Rsinθ.

The change in gravitational potential energy of m1 is
ΔU1=−m1gh1=−m1gRθ
(since m1 loses its potential energy as it falls down).
The change in gravitational potential energy of m2 is
ΔU2=m2gh2=m2gRsinθ
(since m2 gains potential energy as it rises up)
⇒ The total change in gravitational potential energy=
ΔU=ΔU1+ΔU2 (i)
⇒ΔU=−m1gRθ+m2gRsinθ=gR(m2sinθ−m1θ).
The change in KE of the system (m1+m2),
ΔK=12m1v2+12m2v2=(m1+m2)v22 (ii)
where v=speed of m1 and m2 at the positions as shown in the figure.
From the principle of conservation of energy we obtain,
ΔK+ΔU=0 (iii)
Using (i), (ii) and (iii), we obtain,
12(m1+m2)v2−gR(m1θ−m2sinθ)=0
⇒v=√2gR(m1θ−m2sinθ)(m1+m2)
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WORK, POWER & ENERGYEXERCISE - Exercise 8.416videos
WORK, POWER & ENERGY
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WORK, POWER & ENERGYEXERCISE - Exercise 8.515videos
WORK, POWER & ENERGY
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WORK, POWER & ENERGYEXERCISE - Exercise 8.225videos
WORK, POWER & ENERGY
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - VECTORSEXERCISE - Exercise Multiple Correct5videos
VECTORS
Similar Questions
Two beads of masses m1andm2 connected by an inextensible string are kept at rest at the horizontal diametrical points of a fixed smooth vertical semicircular tube. If the beads are released from the given position, find their speeds as the function of vertical distance y converted by mass m2.
 View Solution
View SolutionTwo beads of masses m1andm2 connected by an inextensible string are kept at rest at the horizontal diametrical points of a fixed smooth vertical semicircular tube. If the beads are released from the given position, find their speeds as the function of vertical distance y converted by miss m2.
 View Solution
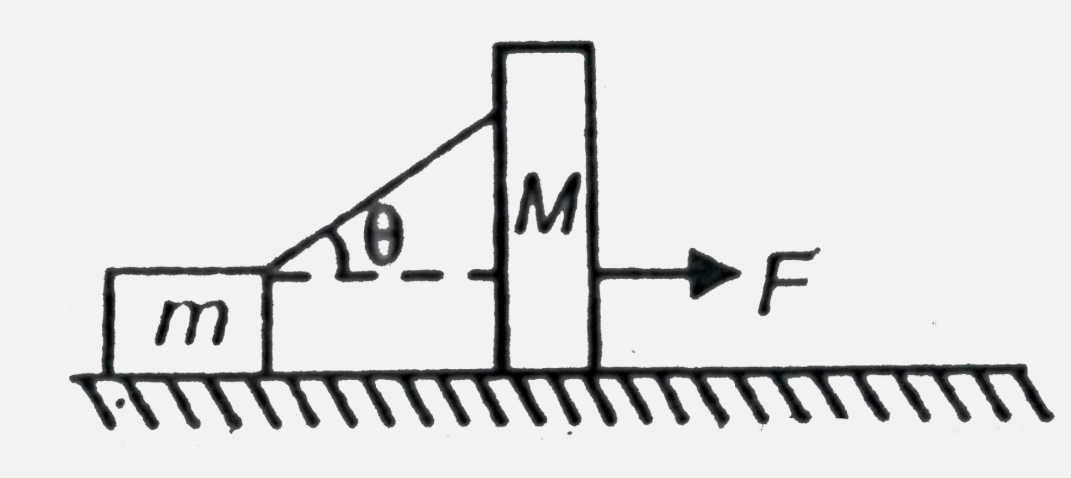
View SolutionTwo blocks of masses m and M are connected by an inextensible light string . When a constant horizontal force acts on the block of mass M. The tension in the string is
 View Solution
View SolutionTwo smooth blocks of masses m and m' connected by a light inextensible strings are moving on a smooth wedge of mass M. If a force F acts on the wedge the blocks do not slide relative to the wedge. Find the (a) acceleration of the wedge and (b) value of F.
 View Solution
View SolutionTwo smooth blocks of masses m and m' connected by a light inextensible strings are moving on a smooth wedge of mass M. If a force F acts on the wedge the blocks do not slide relative to the wedge. Find the (a) acceleration of the wedge and (b) value of F.
 View Solution
View SolutionTwo smooth blocks of masses m and m' connected by a light inextensible strings are moving on a smooth wedge of mass M. If a force F acts on the wedge the blocks do not slide relative to the wedge. Find the (a) acceleration of the wedge and (b) value of F.
 View Solution
View SolutionTwo particles of masses m1andm2 are connected to a string and the system is rotated in a horizontal plane with 'P' as center. The ratio of tension in the two parts of string is
 View Solution
View SolutionTwo identical balls each of mass m interconnected by a small light inextensible string are kept on a smooth horizontal surface. One of the balls is pushed towards the other with a speed v0 find the loss of K.E. of the ball. What will be the final velocities of the balls ? (e=1).
 View Solution
View SolutionTwo particles each of mass m are connected by a light inextensible string and a particle of mass M is attached to the midpoint of the string. The system is at rest on a smooth horizontal table with string just taut and in a straight line. The particle M is given a velocity v along the table perpendicular to the string. Prove that when the two particles are about to collide :
(i) The velocity of M is Mv(M+2m)
(ii) The speed of each of the other particles is (√2M(M+m)(M+2m))v.View SolutionTwo blocks of masses m1 and m2 are connected by a massless spring and placed on smooth surface. The spring initially stretched and released. Then :
View Solution

