In figure, an inextensible string that connects two bodies of mass M and m, passing over a fixed smooth pulley. The body M slides along a smooth vertical rigid bar. If the body M is released from the given position, find the maximum distance raised by body m.

Here we can use ΔK+ΔU=0.
Since initially, the system is at rest and finally it comes to rest (instaneously), the change of KE of the system is zero.
⇒ΔK=0
Also ΔU=0.
⇒(ΔU)M+(ΔU)m=0
Since the block m rises through a height h (say),
(ΔU)m=mgh
Similarly, the change in PE of the mass M is Mgh′, as it falls through a height h′, say
⇒mgh+(−Mgh′)=0⇒h′=mMh (i)
When the mass m ascends through a distance h, the length of the string between the pulley and the bar will be equal to (a+h).
Therefore, h′=√(a+h)2−a2⇒h′=√h(2a+h) (ii)
Eliminating h′ from (i) and (ii), we obtain
√h(2a+h)=mMh
⇒2a+h=m2M2h⇒h=2a(m2M2−1)
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WORK, POWER & ENERGYEXERCISE - Exercise 8.416videos
WORK, POWER & ENERGY
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WORK, POWER & ENERGYEXERCISE - Exercise 8.515videos
WORK, POWER & ENERGY
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WORK, POWER & ENERGYEXERCISE - Exercise 8.225videos
WORK, POWER & ENERGY
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - VECTORSEXERCISE - Exercise Multiple Correct5videos
VECTORS
Similar Questions
Two bodies of masses m1andm2(<m1) are connected to the ends of a massless cord and allowed to move as shown in figure. The pulley is both massless and frictionless. The acceleration of the centre of mass is (m1−m2)n(m1+m2)2g. Find the value of n.
 View Solution
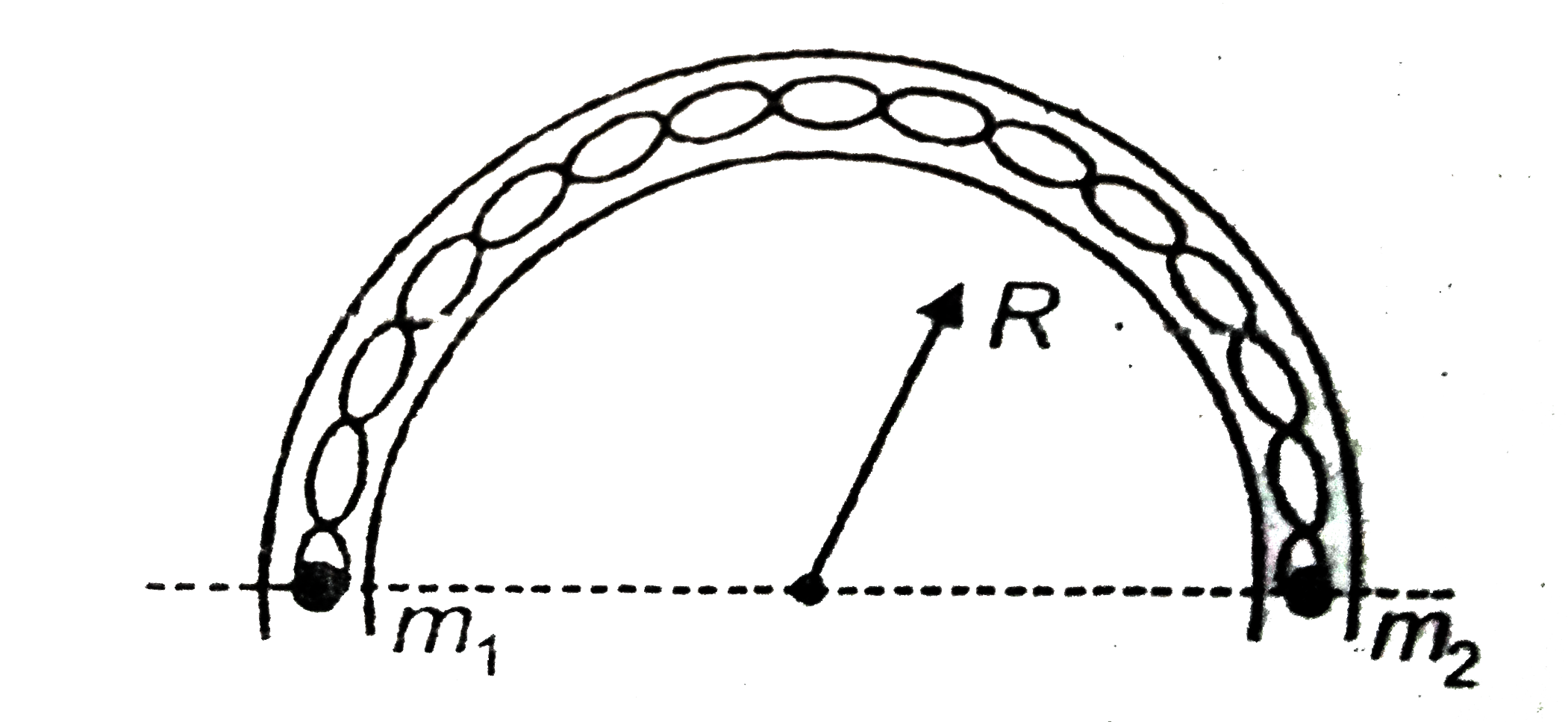
View SolutionTwo beads of masses m1andm2 connected by an inextensible string are kept at rest at the horizontal diametrical points of a fixed smooth vertical semicircular tube. If the beads are released from the given position, find their speeds as the function of vertical distance y converted by mass m2.
 View Solution
View SolutionTwo beads of masses m1andm2 connected by an inextensible string are kept at rest at the horizontal diametrical points of a fixed smooth vertical semicircular tube. If the beads are released from the given position, find their speeds as the function of vertical distance y converted by miss m2.
 View Solution
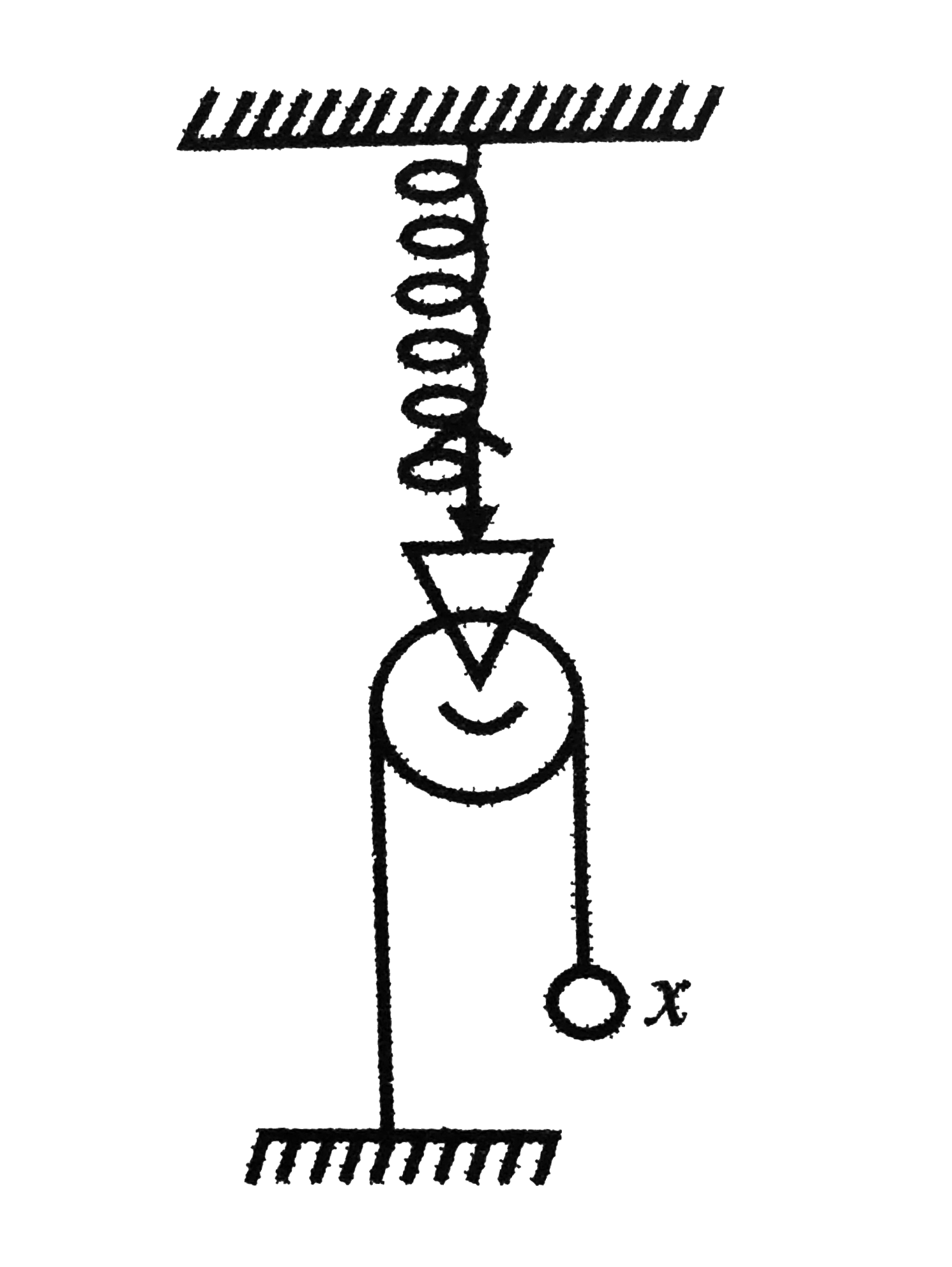
View SolutionA body of mass m hangs by an inextensible string that passes over a smooth mass less pulley that is fitted with a light spring of stiffness k as shown in figure. If the body is released from rest and the spring is released, calculate the maximum elongation of the spring.
 View Solution
View SolutionA light string passing over a smooth light pulley connects two blocks of masses m1 and m2 (vertically). If the acceleration of the system is g/8, then the ratio of the masses is
View SolutionA light string passing over a smooth light pulley connects two blocks of masses m1 and m2 (vertically). If the acceleration of the system is g/8, then the ratio of the masses is
View SolutionTwo blocks are connected by a long inextensible string passing over an ideal pulley as shown in the figure. If the system is released from rest then the common speed of blocks when block m2 moves a distance I will be
View SolutionA ring of mass m = 0.3kg can slide freely on smooth vertical rod. A light and inextensible string is connected to the ring and passes over a smooth and fixed pulley as shown in the figure. The distance of the pulley from the rod is 0.8m and the other end of the string is connected to a block of mass M = 0.5kg. The ring is held in level with pulley and then released from rest.
The distance by which the ring moves down before coming to rest for the first time is 0.75K. Find K.
 View Solution
View SolutionTwo bodies of masses 1 kg and 2 kg are connected by a very light string passed over a clamped light smooth pulley. If the system is released from rest, find the acceleration of the two masses and the tension in the string
View SolutionThe figure an L shaped body of mass M placed on smooth horizontal surface. The block A is connected to the body by means of an inexiensible string , which is passing over a smooth pulley of negligible mass.Another block B of mass m is placed against a vertical wall of the body. Find the minimum value of the mass of block A so that B remain stationary relative to the wall. Coefficient of friction between the block B and the vertical wall is μ.
 View Solution
View Solution

