A particle is acted by x force F=Kx where K is a(+ve) constant its potential energy at x=0 is zero . Which curve correctly represent the variation of potential energy of the block with respect to x
(a) 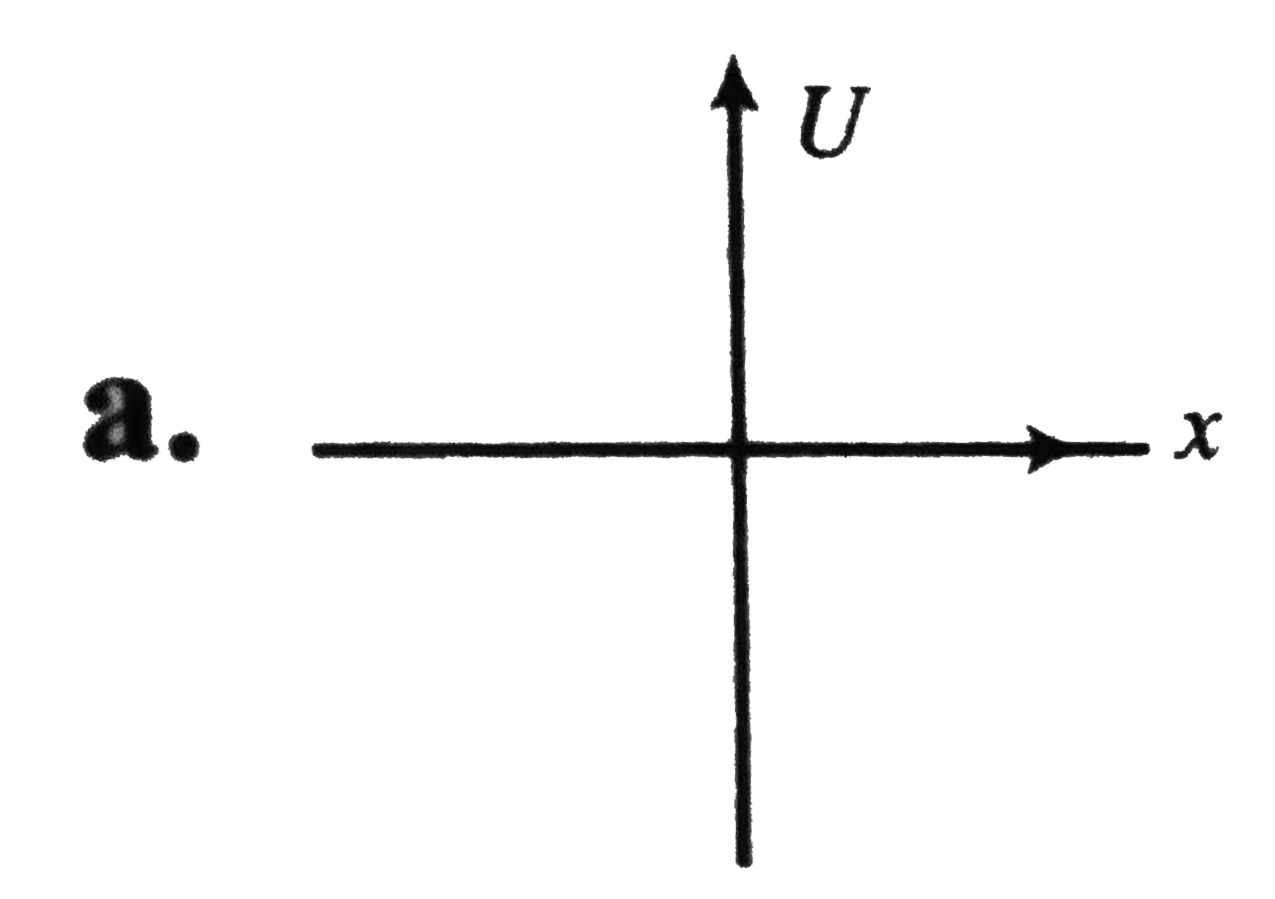
(b) 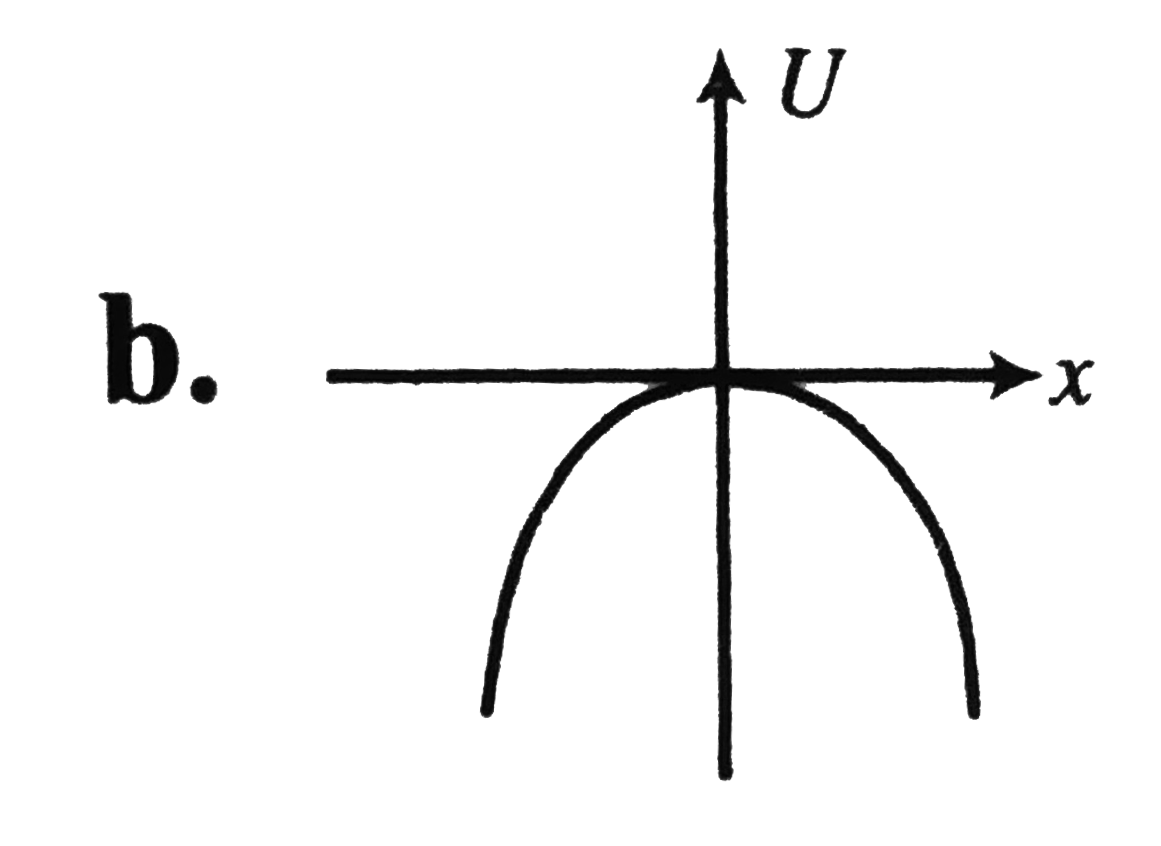
(c) 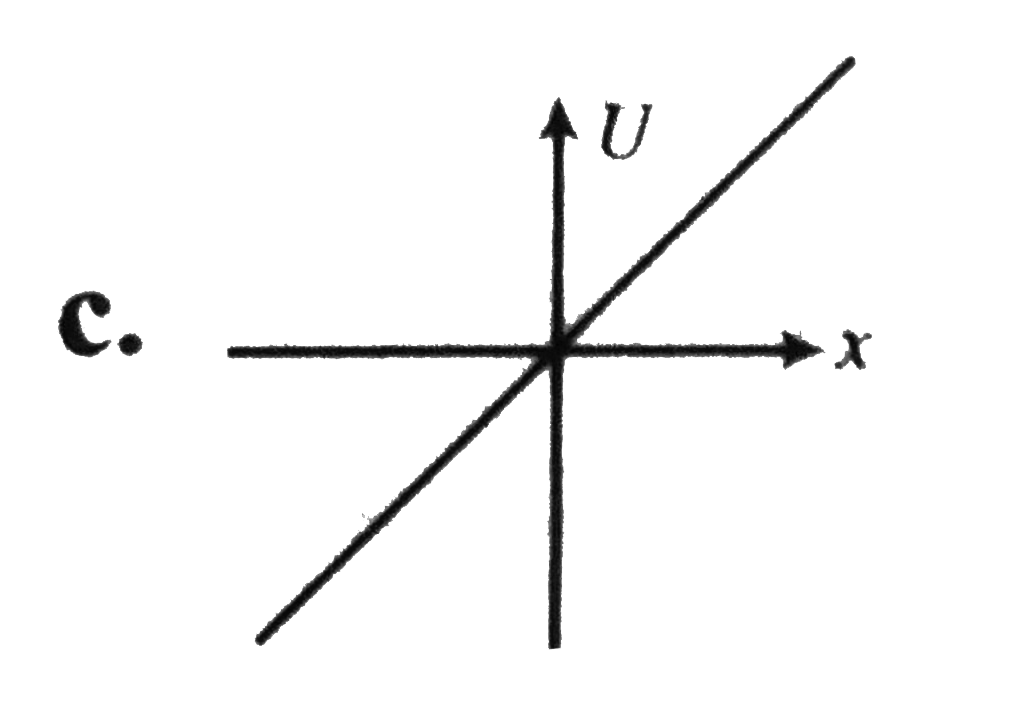
(d) 
The correct Answer is:B
To solve the problem, we need to determine the potential energy (U) of a particle acted upon by a force given by F=Kx, where K is a positive constant. The potential energy at x=0 is specified to be zero.
1. Understand the relationship between force and potential energy:
The force acting on the particle is related to the potential energy by the equation:
F=−dUdx
This means that the force can be expressed as the negative gradient of the potential energy.
2. Substitute the given force into the equation:
We know that F=Kx. Therefore, we can write:
Kx=−dUdx
3. Rearranging the equation:
Rearranging gives us:
dUdx=−Kx
4. Integrate to find potential energy:
To find U, we integrate with respect to x:
U=−∫Kxdx
Performing the integration:
U=−(K2x2)+C
where C is the constant of integration.
5. Determine the constant of integration:
We know that the potential energy at x=0 is zero:
U(0)=0=−(K2(0)2)+C
This implies that C=0.
6. Final expression for potential energy:
Thus, the potential energy as a function of x is:
U(x)=−K2x2
7. Interpret the result:
The expression U(x)=−K2x2 indicates that the potential energy is a downward-opening parabola (an inverted parabola) with respect to x.
Conclusion:
The variation of potential energy U with respect to x is represented by a curve that is an inverted parabola.
The force acting on the particle is related to the potential energy by the equation:
F=−dUdx
This means that the force can be expressed as the negative gradient of the potential energy.
We know that F=Kx. Therefore, we can write:
Kx=−dUdx
Rearranging gives us:
dUdx=−Kx
To find U, we integrate with respect to x:
U=−∫Kxdx
Performing the integration:
U=−(K2x2)+C
where C is the constant of integration.
We know that the potential energy at x=0 is zero:
U(0)=0=−(K2(0)2)+C
This implies that C=0.
Thus, the potential energy as a function of x is:
U(x)=−K2x2
The expression U(x)=−K2x2 indicates that the potential energy is a downward-opening parabola (an inverted parabola) with respect to x.
The variation of potential energy U with respect to x is represented by a curve that is an inverted parabola.
Topper's Solved these Questions
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WORK, POWER & ENERGYEXERCISE - Archives(multiple Correct)
3 Videos
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WORK, POWER & ENERGYEXERCISE - Archives (assertion-reasoning)
1 Videos
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WORK, POWER & ENERGYEXERCISE - Integer
14 Videos
- VECTORSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - VECTORSEXERCISE - Exercise Multiple Correct
5 Videos
Similar Questions
Which of the following curves correctly represent the variation of capacitve reactance (XC) with frequency (f) ?
View SolutionA particle free to move along x-axis is acted upon by a force F=−ax+bx2whrteaandbarepositiveconstants., the correct variation of potential energy function U(x) is best represented by.
View SolutionA body moves from rest with a constant acceleration. Which one of the following graphs represents the variation of its kinetic energy K with the distance travelled x?
View SolutionA body moves from rest with a constant acceleration. Which one of the following graphs represents the variation of its kinetic energy K with the distance travelled x?
View SolutionThe magnitude of gravitational potential energy of the moon earth system is U with zero potential energy at infinite separation. The kinetic energy of the moon with respect to the earth is K.
View SolutionA particle is placed at the origin and a force F=Kx is acting on it (where k is a positive constant). If U(0)=0, the graph of U(x) verses x will be (where U is the potential energy function.)
View SolutionA particle is placed at the origin and a force F=Kx is acting on it (where k is a positive constant). If U(0)=0, the graph of U(x) verses x will be (where U is the potential energy function.)
View SolutionAssuming that potential energy of spring is zero when it is stretched by x02, its potential energy when it is compressed by x0 is
View SolutionA conservative force held function is given by F=k/r2, where k is a constant.
a. Determine the potential energy funciton U(r) assuming zero potential energy at r=r0.
b. Also, determine the potential energy at r=∞.
View SolutionKinetic energy of a particle on the surface of earth is E0 and the potential energy is −2E0.
(a) Will the particle escape to infinity ?
(ii) What is the value of potential energy where speed of the particle becomes zero?
View Solution
