From the top of a building 60m high the angles of depression of the top and the bottom of a tower are observed to be 30o and 60o . Find the height of the tower.
To solve the problem step by step, we will first visualize the scenario and then apply trigonometric principles to find the height of the tower.
1. Draw the Diagram:
- Let the height of the building be AB=60m.
- Let the height of the tower be BC=h.
- The point D is the bottom of the tower.
- The angles of depression from point A (top of the building) to point C (top of the tower) and point D (bottom of the tower) are 30∘ and 60∘ respectively.
2. Identify the Relationships:
- The angle of depression to the top of the tower C is 30∘.
- The angle of depression to the bottom of the tower D is 60∘.
3. Use Trigonometric Ratios:
- From the angle of depression to point C:
tan(30∘)=AB−BCAD=60−hx
Where x is the horizontal distance from the building to the tower.
- From the angle of depression to point D:
tan(60∘)=ABAD=60x
4. Substituting Values:
- We know that tan(30∘)=1√3 and tan(60∘)=√3.
- From the first equation:
1√3=60−hx⟹x=√3(60−h)
- From the second equation:
√3=60x⟹x=60√3=20√3
5. Equating the Two Expressions for x:
- Set the two expressions for x equal to each other:
√3(60−h)=20√3
- Dividing both sides by √3:
60−h=20
6. Solving for h:
- Rearranging gives:
h=60−20=40
7. Conclusion:
- The height of the tower BC is 40m.
Final Answer:
The height of the tower is 40 meters.
---
- Let the height of the building be AB=60m.
- Let the height of the tower be BC=h.
- The point D is the bottom of the tower.
- The angles of depression from point A (top of the building) to point C (top of the tower) and point D (bottom of the tower) are 30∘ and 60∘ respectively.
- The angle of depression to the top of the tower C is 30∘.
- The angle of depression to the bottom of the tower D is 60∘.
- From the angle of depression to point C:
tan(30∘)=AB−BCAD=60−hx
Where x is the horizontal distance from the building to the tower.
tan(60∘)=ABAD=60x
- We know that tan(30∘)=1√3 and tan(60∘)=√3.
- From the first equation:
1√3=60−hx⟹x=√3(60−h)
- From the second equation:
√3=60x⟹x=60√3=20√3
- Set the two expressions for x equal to each other:
√3(60−h)=20√3
- Dividing both sides by √3:
60−h=20
- Rearranging gives:
h=60−20=40
- The height of the tower BC is 40m.
The height of the tower is 40 meters.
Topper's Solved these Questions
Similar Questions
From the top of a 50 m high tower, the angles of depression of the top and bottom of a pole are observed to be 45o and 60o respectively. Find the height of the pole.
View SolutionFrom the top of a building AB , 60 m high, the angles of depression of the top and bottom of a vertical lamp post CD are observed to be 30o and 60o respectively. Find the height of the lamp post.
View SolutionFrom the top of a building AB , 60 m high, the angles of depression of the top and bottom of a vertical lamp post CD are observed to be 30o and 60o respectively. Find the difference between the heights of the building and the lamp post.
View SolutionFrom the top of a building AB , 60 m high, the angles of depression of the top and bottom of a vertical lamp post CD are observed to be 30o and 60o respectively. Find the horizontal distance between AB and CD
View SolutionFrom the top of a cliff, the angle of depression of the top and bottom of a tower are observed to be 45∘ and 60∘ respectively. If the height of the tower is 20 m.
Find :
(i) the height of the cliff
(ii) the distance between the cliff and the tower.
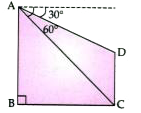
View SolutionIn the figure given, from the top of a building AB = 60 m high, the angles of depression of the top and bottom of a vertical lamp post CD are observed to be 30∘and60∘ respectively. Find :
(ii) the height of the lamp post.
View SolutionIn the given figure, A from the top of a building AB = 60 m high, the angles of depression of the top and bottom of a vertical lamp post CD are observed to be 30∘and60∘ respectively. Find :
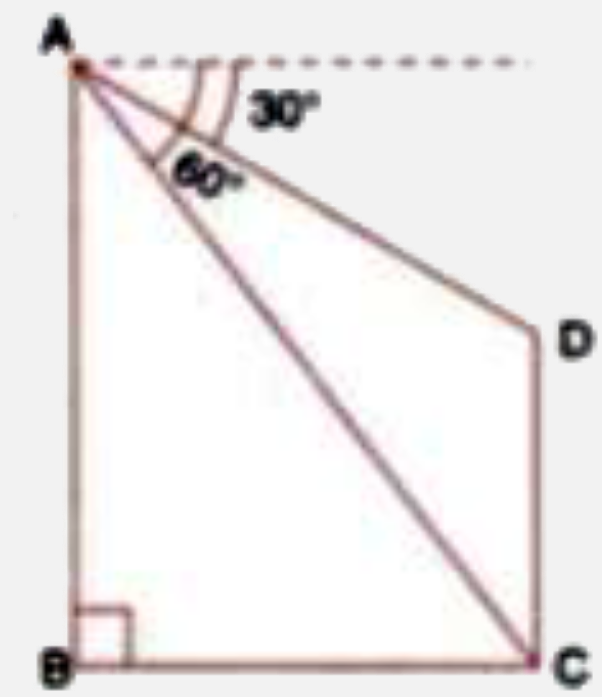
the horizontal distance between AB and CD
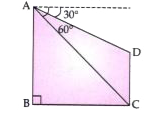
View SolutionIn the igure given, from the top of a building AB = 60 m high, the angles of depression of the top and bottom of a vertical lamp post CD are observed to be 30∘and60∘ respectively. Find :
(i) the horizontal distance between AB and CD.
View SolutionFrom te top of a tower , 60 meters high, the angles of depression of the top and bottom of a pole are αandβ respectively .Find the height of the pole.
View SolutionIf from the top of a tower 80 meters high the angles of depression of the top and bottom of a house are 30∘and45∘ respectively, then the height of the house is
View Solution
