A circular hole of radius $R / 2$ is cut from a circular disc of radius $R$ . The disc lies in the $x y$ -plane and its centre coincides with the origin. If the remaining mass of the disc is $M$ , then
a. determine the initial mass of the disc and
b. determine its moment of inertia about the $z$ -axis.

Video Solution

Text Solution

Verified by Experts

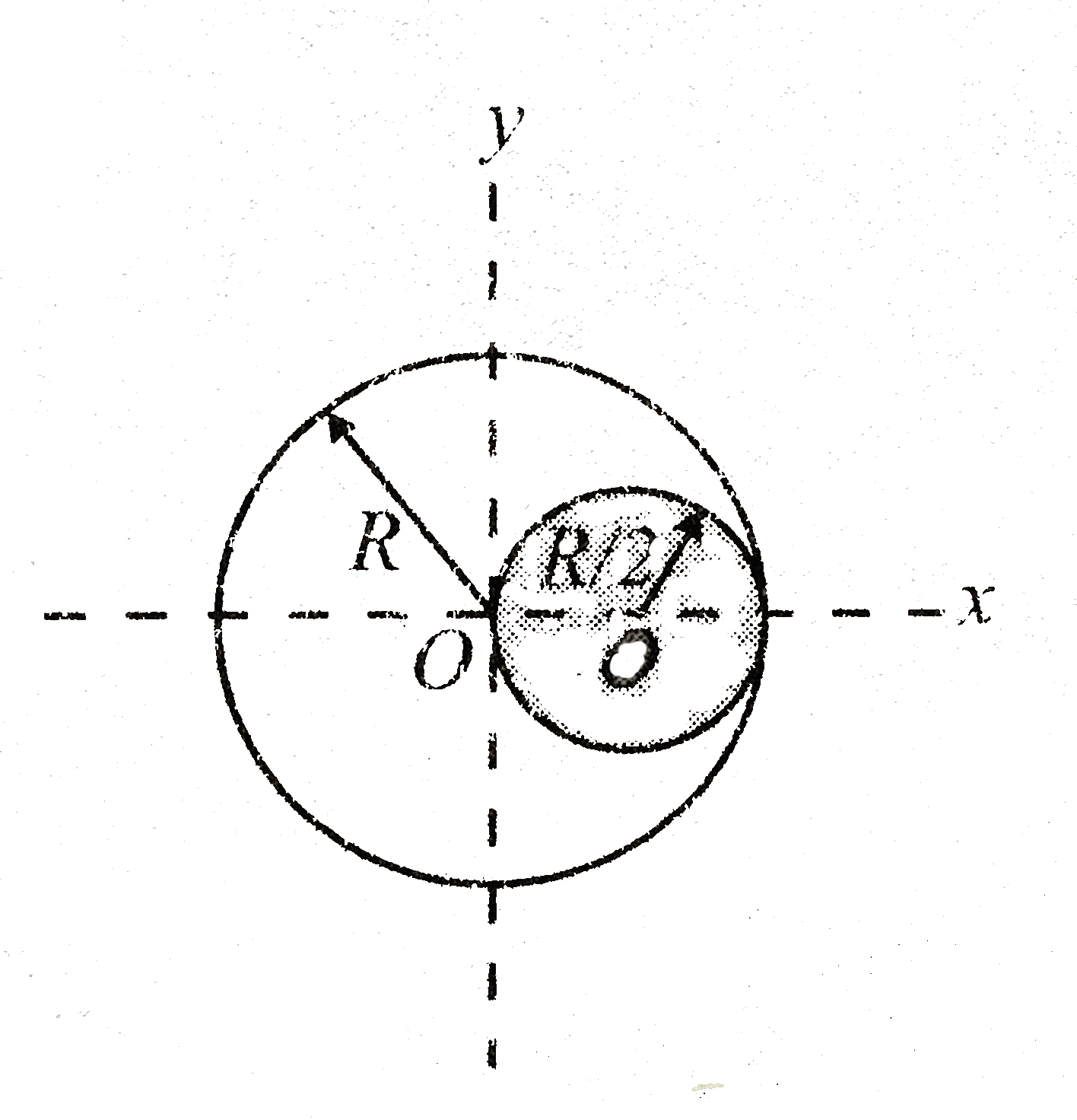
Let $σ$ be the surface mass density of the plate given by
$σ = \frac{M}{{(π R^{2} - π (\frac{R}{2}))}^{2}} = \frac{4}{3} \frac{M}{π R^{2}}$
Now, initial mass of the plate $m_{1} = σ (π R^{2}) = \frac{4}{3} M$
mass of the plate removed $m_{2} = σ (\frac{π R^{2}}{4}) = \frac{M}{3}$
The given arrangement may be considered as a combination of a circular plate of mass $(4 / 3) M$ and circular plate of negative mass $(M / 3) .$

The moment of inertia of the big disc of radius $R$ and mass $m_{1}$ about $O$ and parallel to the $z$ -axis is
$I_{O_{1}} = \frac{m_{1} R^{2}}{2}$
The moment of inertia of the small disc of mass $m_{2}$ and radius $\frac{r}{2}$ about $O$ and parallel to $z$ -axis.
$I_{O_{1}} = \frac{m_{2} {(\frac{R}{2})}^{2}}{2} = \frac{m_{2} R^{2}}{8}$
The moment of inertia of the small disc about $O$ (using parallel axis theorem).
$I_{O_{2}} = \frac{m_{2} R^{2}}{8} + \frac{m_{2} R^{2}}{4} = \frac{3 m_{2} R^{2}}{8}$
As the part of the disc on mass $m_{2}$ is removed from disc $m_{1}$ , hence the net moment of inertia of structure is
$I_{O} = I_{O_{1}} = I (O_{2})$
$I_{O} = \frac{m_{1} R^{2}}{2} - \frac{3 m_{2} R^{2}}{8}$
substituting the values of $m_{1}$ and $m_{2}$ we get
$I_{0} = \frac{13}{24} M R^{2}$

|

Updated on:21/07/2023

Class 11 PHYSICS RIGID BODY DYNAMICS

Topper's Solved these Questions

Similar Questions

CENGAGE PHYSICS ENGLISH-RIGID BODY DYNAMICS 1-Integer

Home
Ask Doubt
Profile