A concentric hole of radius R/2 is cut from a thin circular plate of mass M and radius R. The moment of inertia of the remaining plate about its axis will be
(a)1324MR2
(b)1124MR2
(c)1332MR2
(d)1532MR2
The correct Answer is:D
To find the moment of inertia of a thin circular plate with a concentric hole cut out, we can follow these steps:
Step 1: Define the mass and radius of the original plate
Let the mass of the original circular plate be M and the radius be R.
Step 2: Calculate the mass of the hole
The radius of the hole is R2. The area of the original plate is πR2 and the area of the hole is π(R2)2=πR24.
The mass of the hole can be calculated using the ratio of the areas, assuming uniform density:
Mass of the hole=M×Area of the holeArea of the original plate=M×πR24πR2=M×14=M4
Step 3: Calculate the mass of the remaining plate
The mass of the remaining plate after the hole is cut out is:
Mass of remaining plate=M−M4=3M4
Step 4: Calculate the moment of inertia of the original plate
The moment of inertia I of a thin circular plate about its central axis is given by:
Ioriginal=12MR2
Step 5: Calculate the moment of inertia of the hole
The moment of inertia of the hole about the same axis can be calculated as:
Ihole=12(M4)(R2)2=12⋅M4⋅R24=MR232
Step 6: Use the parallel axis theorem
Since the hole is concentric, we do not need to use the parallel axis theorem. The moment of inertia of the remaining plate is simply the moment of inertia of the original plate minus the moment of inertia of the hole:
Iremaining=Ioriginal−Ihole=12MR2−MR232
Step 7: Simplify the expression
To simplify:
Iremaining=16MR232−MR232=(16M−M)R232=15MR232
Conclusion
The moment of inertia of the remaining plate about its axis is:
Iremaining=15MR232
Let the mass of the original circular plate be M and the radius be R.
The radius of the hole is R2. The area of the original plate is πR2 and the area of the hole is π(R2)2=πR24.
Mass of the hole=M×Area of the holeArea of the original plate=M×πR24πR2=M×14=M4
The mass of the remaining plate after the hole is cut out is:
Mass of remaining plate=M−M4=3M4
The moment of inertia I of a thin circular plate about its central axis is given by:
Ioriginal=12MR2
The moment of inertia of the hole about the same axis can be calculated as:
Ihole=12(M4)(R2)2=12⋅M4⋅R24=MR232
Since the hole is concentric, we do not need to use the parallel axis theorem. The moment of inertia of the remaining plate is simply the moment of inertia of the original plate minus the moment of inertia of the hole:
Iremaining=Ioriginal−Ihole=12MR2−MR232
To simplify:
Iremaining=16MR232−MR232=(16M−M)R232=15MR232
The moment of inertia of the remaining plate about its axis is:
Iremaining=15MR232
Topper's Solved these Questions
Similar Questions
A hole of radius R/2 is removed from a thin circular plate of radius R and mass M. The moment of inertia of the remaining plate about an axis through centre O and perpendicular to the plane of the plate is

View SolutionFour holes of radius R are cut from a thin square plate of side 4R and mass M. The moment of inertia of the remaining portion about z-axis is :
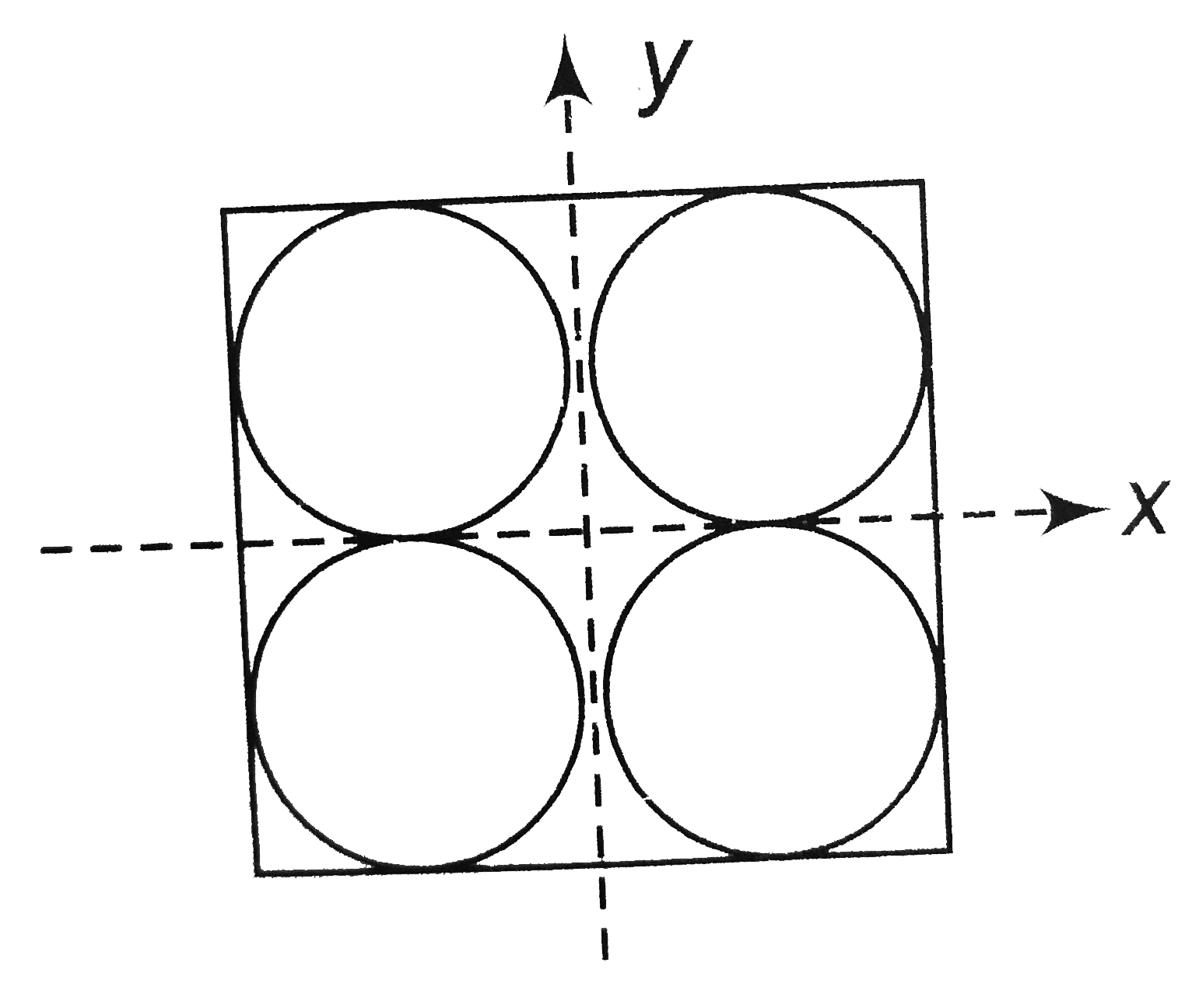 .
.
View SolutionA hole of radius R/2 is cut from a thin circular plate of raduis R as shown in the figure. If the mass of the remaining plate is M, then find moment of inertia of the plate about an axis through O perpendicular to plane

A. 1325MR2
B. 1324MR2
C. 1124MR2
D. 1125MR2
View SolutionThe moment of inertia of a ring of mass M and radius R about PQ axis will be

View SolutionA disc has mass 9 m. A hole of radius R/3 is cut from it as shown in the figure. The moment of inertia of remaining part about an axis passing through the centre 'O' of the disc and perpendicular to the plane of the disc is :

View SolutionFrom a disc of radius R, a concentric circular portion of radius r is cut out so as to leave an annular disc of mass M. The moment of inertia of this annular disc about the axis perpendicular to its plane and passing through its centre of gravity is
View SolutionMoment of inertia of a circular wire of mass M and radius R about its diameter is
View SolutionOut of a disc of mass M and radius R a concentric disc of mass m and radius r is removed. The M.I. of the remaining part about the symmetric axis will be :
View SolutionA wheel comprises a ring of radius R and mass M and three spokes of mass m each. The moment of inertia of the wheel about its axis is

View SolutionFrom a circular disc of radius R and mass 9 M , a small disc of radius R/3 is removed from the disc. The moment of inertia of the remaining disc about an axis perpendicular to the plane of the disc and passing through O is

View Solution
