Three point masses $m_{1}, m_{2}$ and $m_{3}$ are located at the vertices of an equilateral triangle of side $α$ . What is the moment of inertia of the system about an axis along the altitude of the triangle passing through $m_{1} ?$

A

$(m_{1} + m_{2}) \frac{a^{2}}{4}$

B

$(m_{2} + m_{3}) \frac{a^{2}}{4}$

C

$(m_{1} + m_{3}) \frac{a^{2}}{4}$

D

$(m_{1} + m_{2} + m_{3}) \frac{a^{2}}{4}$

Video Solution

Text Solution

Generated By DoubtnutGPT

The correct Answer is:B

To find the moment of inertia of the system of three point masses located at the vertices of an equilateral triangle about an axis along the altitude passing through one of the masses, we can follow these steps:
1. Understand the Configuration:
- We have three point masses $m_{1}, m_{2},$ and $m_{3}$ located at the vertices of an equilateral triangle with side length $α$ .
- Let’s denote the vertices as follows:
- $m_{1}$ at vertex A,
- $m_{2}$ at vertex B,
- $m_{3}$ at vertex C.
2. Identify the Axis of Rotation:
- The axis of rotation is along the altitude from vertex A (where $m_{1}$ is located) to the midpoint of side BC.
3. Calculate the Distance from the Axis:
- The distance from $m_{1}$ to the axis is $0$ because it lies on the axis.
- The distance from $m_{2}$ and $m_{3}$ to the axis can be calculated. The altitude $h$ of the triangle can be calculated using the formula:
$h = \frac{\sqrt{3}}{2} α$
- The distance from the axis to $m_{2}$ and $m_{3}$ is $\frac{α}{2}$ (the horizontal distance from the midpoint of BC to either vertex B or C).
4. Calculate the Moment of Inertia:
- The moment of inertia $I$ about the axis can be calculated using the formula:
$I = I_{1} + I_{2} + I_{3}$
- Since $I_{1} = 0$ (because $m_{1}$ is on the axis), we have:
$I = 0 + I_{2} + I_{3}$
- The contributions from $m_{2}$ and $m_{3}$ are:
$I_{2} = m_{2} {(\frac{α}{2})}^{2} = m_{2} \frac{α^{2}}{4}$
$I_{3} = m_{3} {(\frac{α}{2})}^{2} = m_{3} \frac{α^{2}}{4}$
- Therefore, the total moment of inertia is:
$I = m_{2} \frac{α^{2}}{4} + m_{3} \frac{α^{2}}{4} = \frac{α^{2}}{4} (m_{2} + m_{3})$
5. Final Expression:
- The moment of inertia of the system about the given axis is:
$I = \frac{α^{2}}{4} (m_{2} + m_{3})$

|

Updated on:7/8/2024

Class 11 PHYSICS RIGID BODY DYNAMICS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
Three point masses each of mass m are placed at the corners of an equilateral triangle of side b. The moment of inertia of the system about an axis coinciding with one side of the triangle is

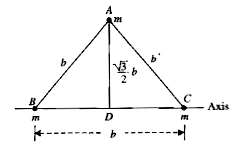A $3 m b^{2}$
B $m b^{2}$
C $(3 / 4) m b^{2}$
D $(2 / 3) m b^{2}$
Question 2 - Select One
Three particles of masses $1 k g, \frac{3}{2} k g, and 2 k g$ are located the vertices of an equilateral triangle of side $a$ . The $x, y$ coordinates of the centre of mass are.
Aa. $\frac{5 a}{9}, \frac{2 a}{3 \sqrt{3}}$
Bb. $\frac{2 a}{3 \sqrt{3}}, \frac{5 a}{9}$
Cc. $\frac{5 a}{9}, \frac{2 a}{\sqrt{3}}$
Dd. $\frac{2 a}{\sqrt{3}}, \frac{5 a}{9}$

CENGAGE PHYSICS ENGLISH-RIGID BODY DYNAMICS 1-Single Correct

Home
Ask Doubt
Profile