A disc of radius R rolls without slipping at spped v along positve x-axis. Velocity of point P at the instant shown in figure is
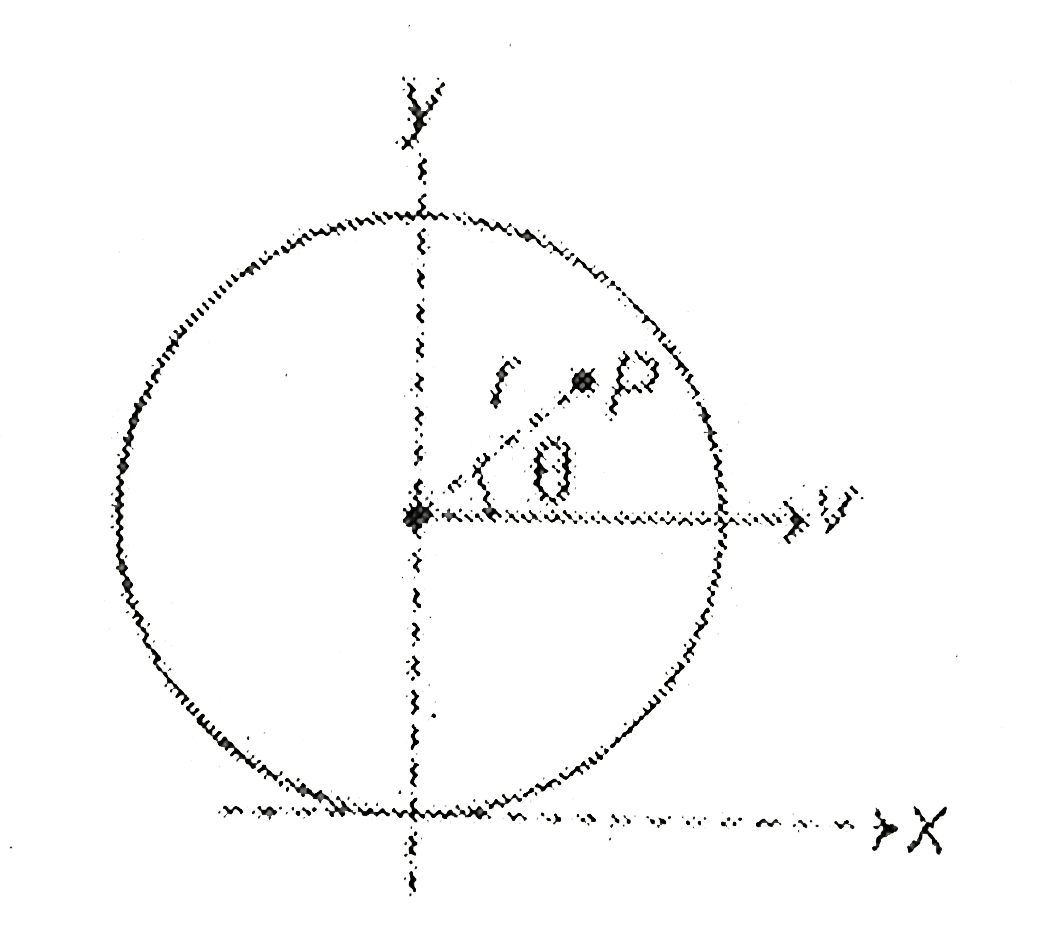
→VP=(v+vrsinθR)ˆi+vrcosθRˆj
→VP=(v+vrsinθR)ˆi−vrcosθRˆj
→VP=vrsinθRˆi+vrcosθRˆj
→VP=vrsiθRˆi−vrcosθRˆj
The correct Answer is:B
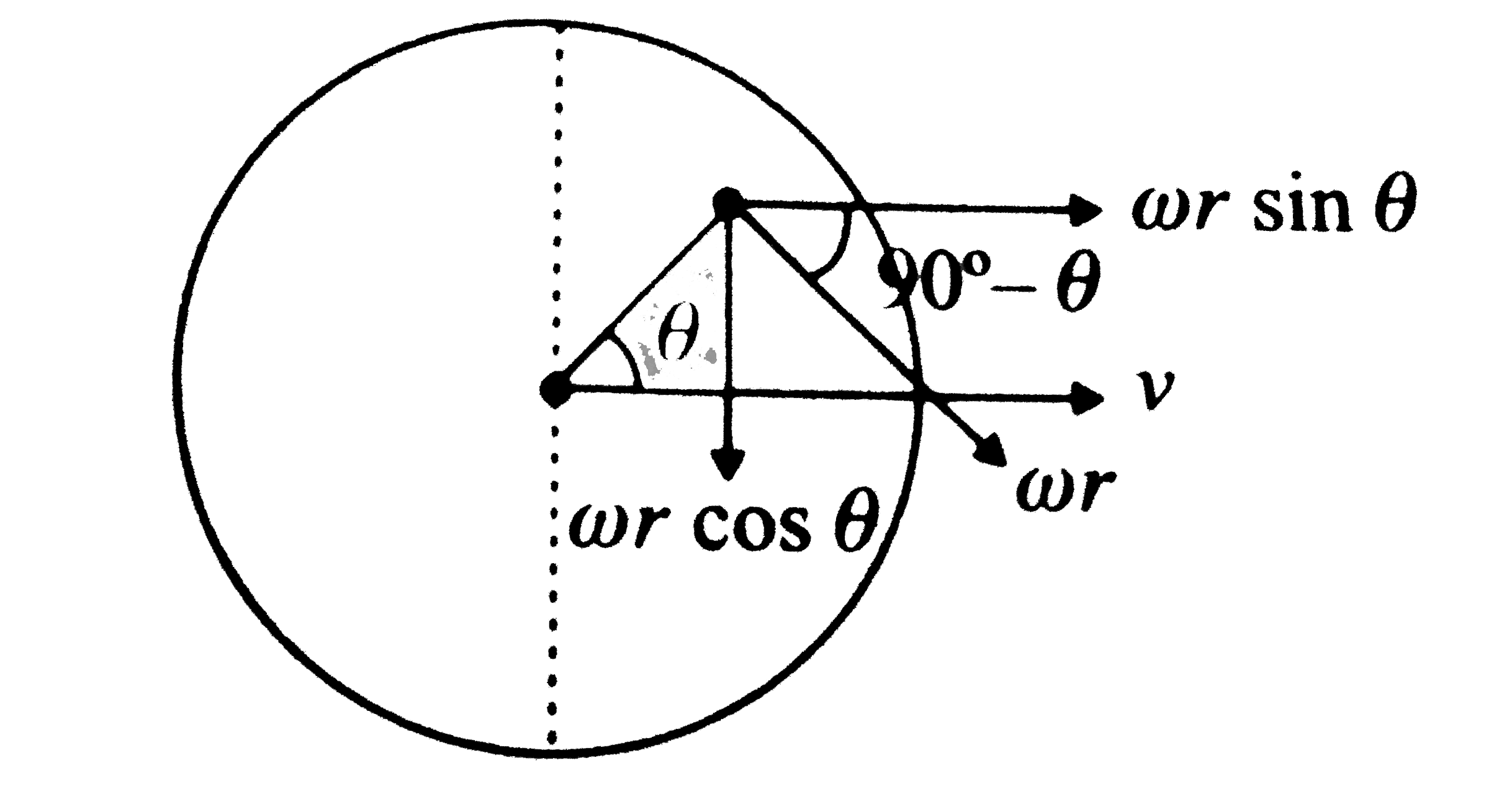
Here ω=vR
vPx=(v+vRrsinθ)ˆi
VPy=(vRrcosθ)ˆj
∴→VP=(v+vrsinθR)ˆi−vrcosrθRˆj
=(v+vrsiθr)ˆi−vrcosθRˆj
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Multiple Correct9videos
RIGID BODY DYNAMICS 1
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Linked Comprehension28videos
RIGID BODY DYNAMICS 1
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Subjective13videos
RIGID BODY DYNAMICS 1
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - INTEGER_TYPE2videos
PROPERTIES OF SOLIDS AND FLUIDS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Interger2videos
RIGID BODY DYNAMICS 2
Similar Questions
A disc of radius R rolls without slipping at speed v along positive x-axis. Velocity of point P at the instant shown in Fig. is
 View Solution
View SolutionDuring rolling without slipping, what is the velocity of the point in contact with the surface.
View SolutionA circular disc of radius R rolls without slipping along the horizontal surface with constant velocity v0 . We consider a point A on the surface of the disc. Then, the acceleration of point A is
View SolutionA ring rolls without slipping on a horizontal surface. At any instant its position is as shown in the figure.
View SolutionA wheel of radius r rolls without slipping with a speed v on a horizontal road. When it is at a point A on the road, a small blob of mud separates from'the wheel at- its highest point and lands at point B on the road:
View SolutionA wheel of radius r rolls without slipping with a speed v on a horizontal road. When it is at a point A on the road, a small blob of mud separates from'the wheel at- its highest point and lands at point B on the road:
View SolutionA disc of mass m and radius R is rolling without slipping as shown in the figure. The magnitude of net velocity of the point P is (OP=R2)
View SolutionA disc of radius r rolls without slipping on a rough horizontal floor. If veloocity of its centre of mass is v0, then velocity of point P, as shown in the figure
(OP=r/2 and ∠QOP=60∘)is
 View Solution
View SolutionA disc of radius R is rolling without sliding on a horizontal surface with a velocity of center of mass v and angular velocity ω in a uniform magnetic field B which is perpendicular to the plane of the disc as shown in Fig. 3.179. O is the center of the disc and P,Q,R,andS are the four points on the disc. Which of the following statements is true?
 View Solution
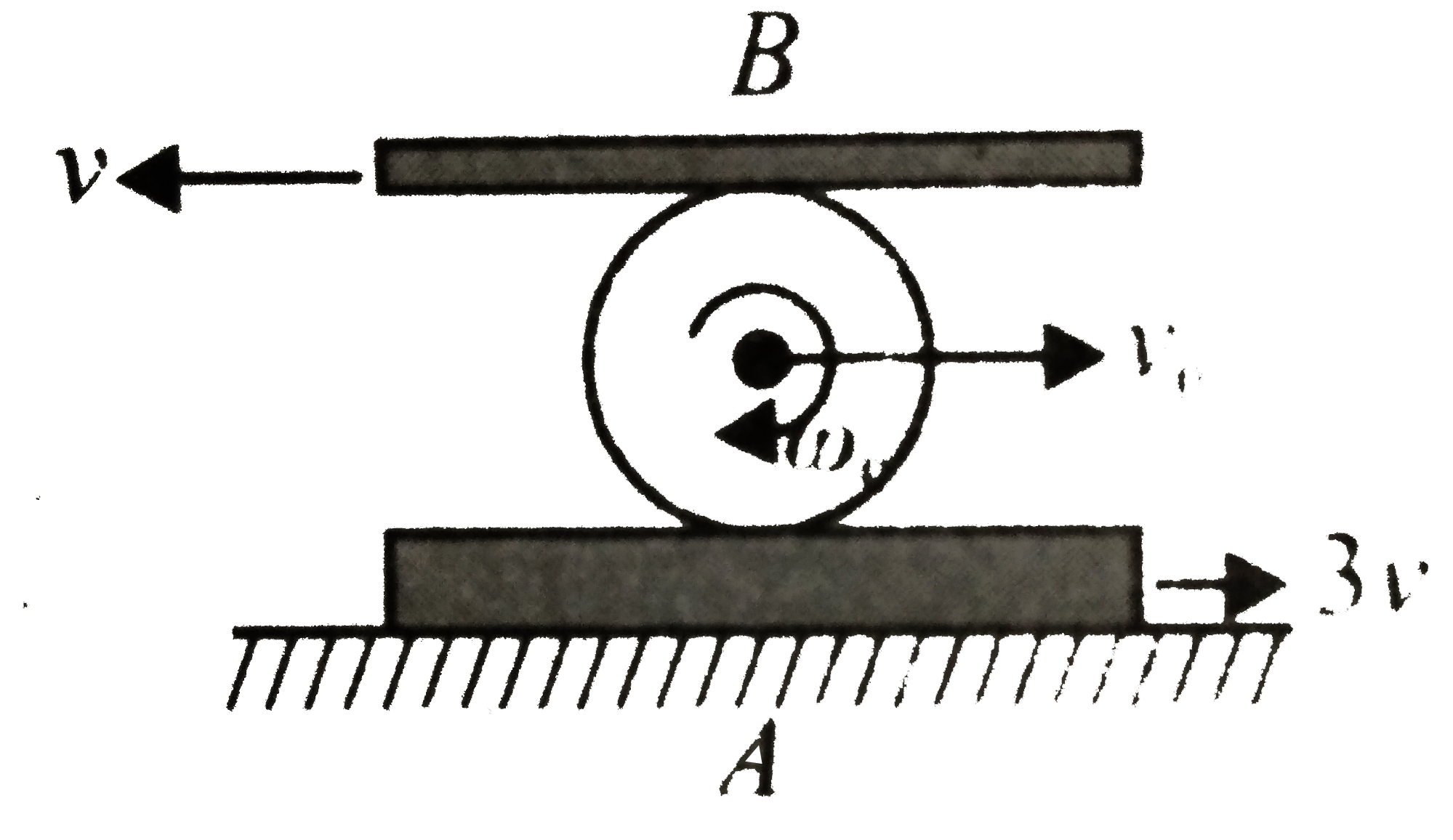
View SolutionThe disc of radius r is confined to roll without slipping at A and B. If the plates have the velocities shown, then
 View Solution
View Solution


