A hoop of mass m is projected on a floor with linear velocity v0 and reverse spin ω0. The coefficient of friction between the hoop and the ground is μ.
a. Under what condition will the hoop return back?
b. How far will it go?
c. How long will it continue to slip when its centre of mass becomes stationary?
d. What is the velocity of return?
a. The acceleration of hoop, a=−μg
Angular acceleration of wheel =mgR
Linear velocity at time t,v=v0−μgt……….i
Angular velocity at time ω=ω0−mgRt…….ii
Let linear velocity be zero at t
So, 0=v0−μgt or t1=v0mg
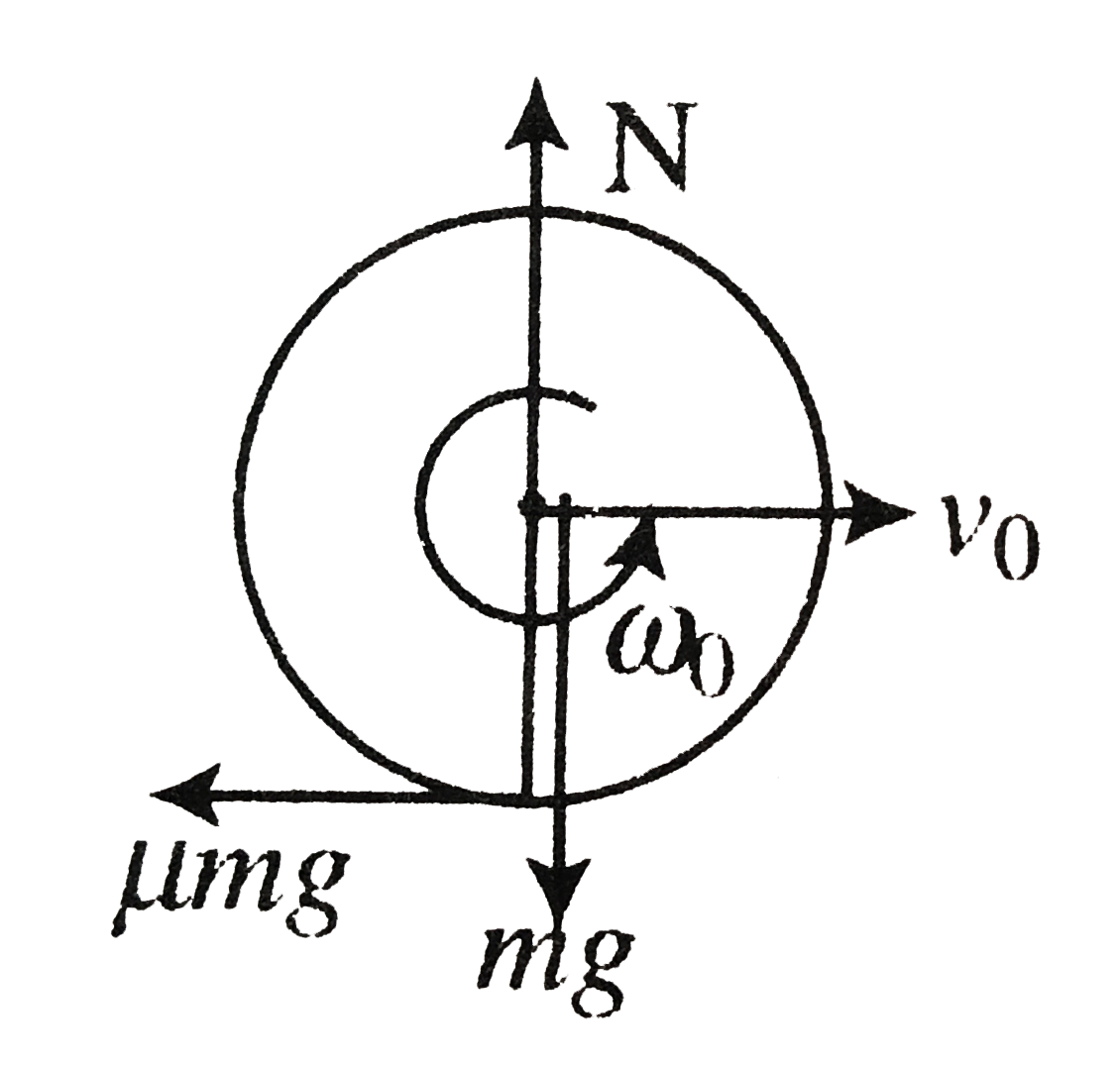
Angular velocity of the ring at t is
ω=ω0−(μgR)(v0μg)=ω0−v0R.......iii
The hoop will return if it has reverse spin at the instant its linear velocity is zero. So the condition for hop to return is
ω0−v0R>0 or ω0>v0R
b. Let t2 be the time up to which the hoop slips on the floor and v be the return velocity.
Then v=μgt2 and ω'=ω−μgRt2
For no slip condition is achieved when
μgRt2=ω−μgRt2⇒2μgRt2=ω......iv
From eqn iii and iv 2μgRt2=ω=ω0−v0R
or t2=R2μg(ω0−v0R)
c. V=μgt2=ω0R2−v02
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Exercise 3.111videos
RIGID BODY DYNAMICS 2
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Exercise 3.213videos
RIGID BODY DYNAMICS 2
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Interger2videos
RIGID BODY DYNAMICS 2
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Integer11videos
RIGID BODY DYNAMICS 1
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOUND WAVES AND DOPPLER EFFECTEXERCISE - Integer16videos
SOUND WAVES AND DOPPLER EFFECT
Similar Questions
A body of mass m is pushed with the initial velocity v0 up an inclined plane of angle of inclination θ. The co-efficient or friction between the body and the plane is μ. What is the net work done by fnction during the ascent of the body before it comes to stop ?
View Solution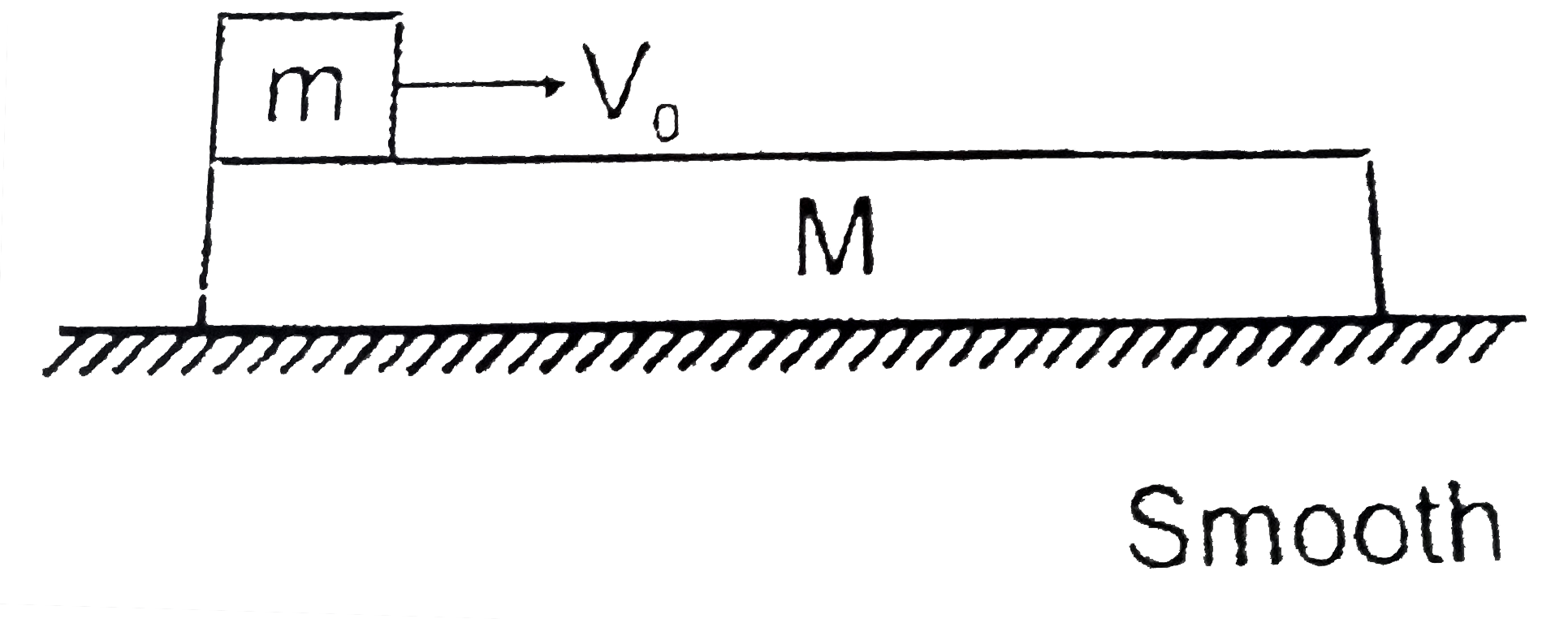
The block of mass m is kept on plank of mass M. The block is given velocity V0 as shown. The coefficient of friction between the block of mass m and plank of mass M is μ and its value is such that block becomes stationary with respect to plank before it reaches the other end. Then:View SolutionA block of mass m is projected up with a velocity v0 along an inclined plane of angle of inclination θ=37∘. The coefficient of friction between the inclined plane AB and blocks is μ(=tanθ). Find the values of v0 so that the block moves in a circular path from B to C.
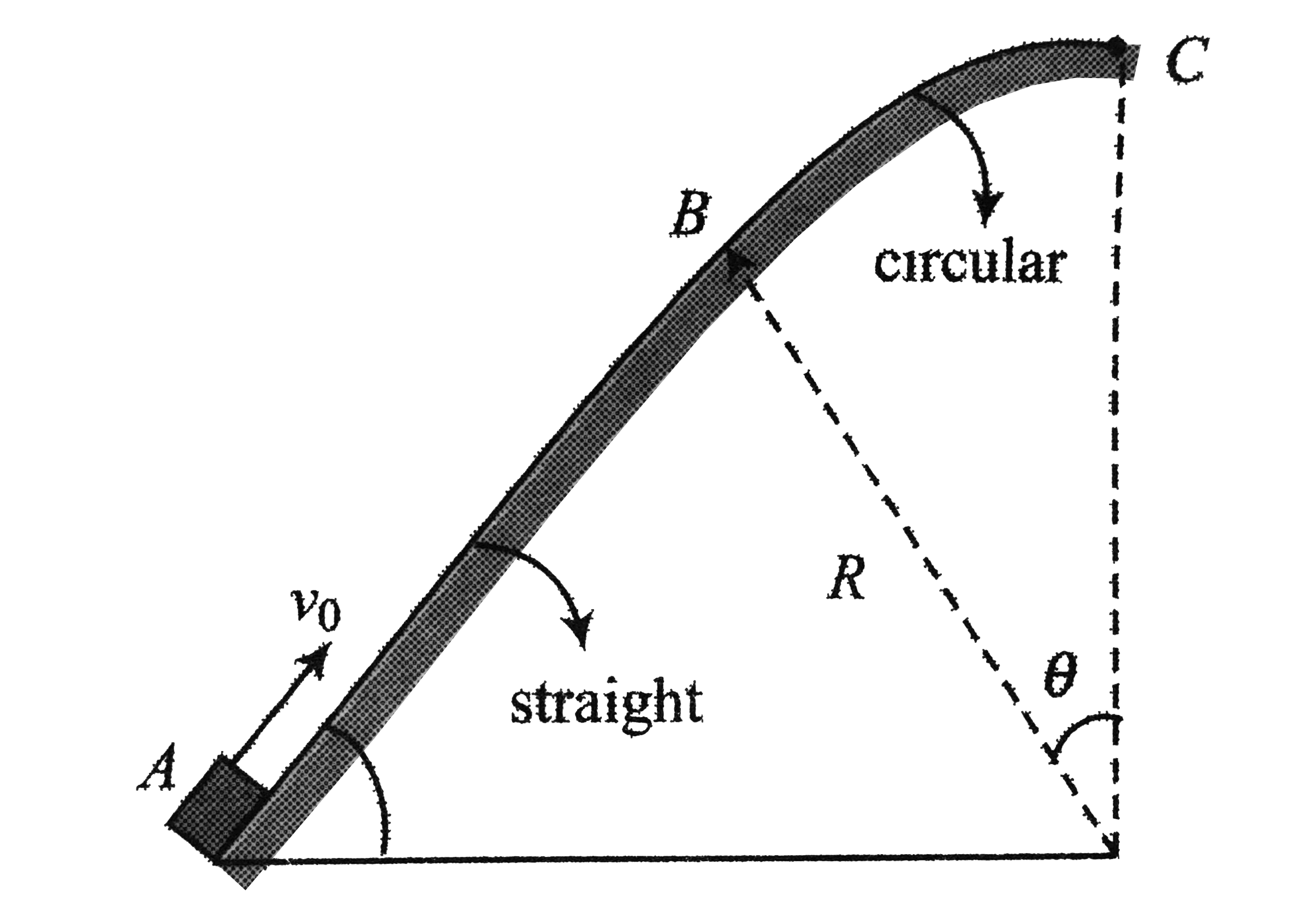 View Solution
View SolutionA plank of mass M and length L is placed at rest on a smooth horizontal surface. A small block of mass m is projected with a velocity v0 from the left end of it as shown in figure. The coefficient of friction between the block and the plank is m, and its value is such that the block becomes stationary with respect to the plank before it reaches the other end.

a. Find the time and common velocity when relative sliding between the block and the plank stops.
b. Find the work done by the friction force on the block during the period it slides on the plank. Is the work positive or negative?
c. Calculate the work done on the plank during the same period. Is the work positive or negative?
d. Also, determine the net work done by friction, Is it positive or negative?View SolutionA small block of mass m is projected on a larger block of mass 10m and length l with a velocity v as shown in the figure. The coefficient of friction between the two block is μ2 while that between the lower block and the ground is μ1. Given that μ2>11μ1.

(a) Find the minimum value of v, such that the mass m falls off the block of mass 10m .
(b) If v has minimum value, find the time taken by block m to do so.View SolutionThe mass of a hoop of radius 0.30 m is 2kg. It rolls along a horizontal floor so that its centre of mass has a speed of 2 m/s. What is the work done to stop it ?
View SolutionA block mass m=2kg is moving with velocityv0 towards a mass less unstretched spring of the force constant k=10N/m. Coefficient of friction between the block and the ground is μ=0.2. Find the maximum value of v0 so that after pressing the spring the block does not return back but stops there permanently.
 View Solution
View SolutionA block of mass m is pushed with a velocity v0 along the surface of a trolley car of mass M. If the horizontal ground is smooth and the coefficient of kinetic friction between the block of plank is μ. Find the minimum distance of relative sliding between the block and plank.
 View Solution
View SolutionOn a stationary block of mass 2kg a horizontal forces F starts acting at t=0 whose veriation with time is shown in figure .The coefficient of friction between the block and ground is 0.5 New answer the following question
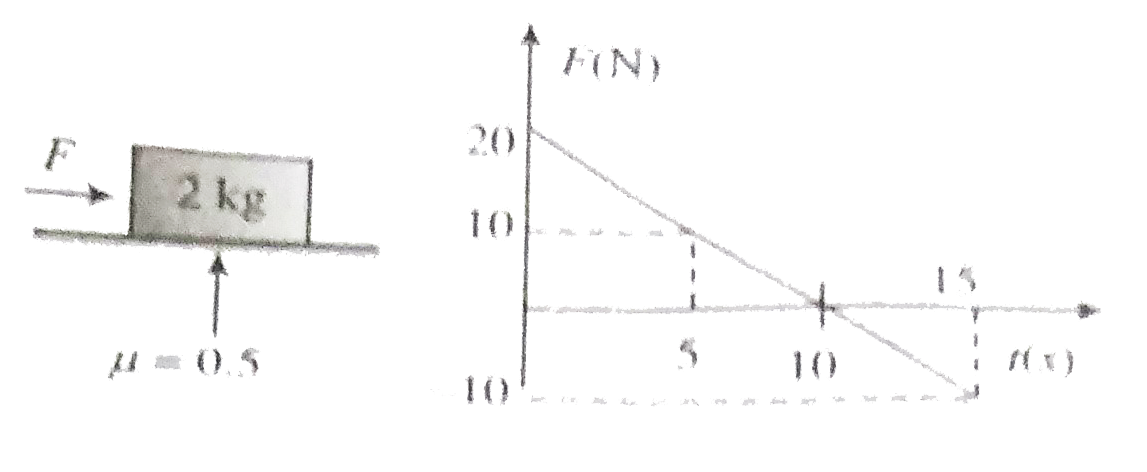
Find the velocity of the block when for the firsst time its acceleration become zeroView SolutionA bullet of mass 50g moving with velocity 600m/s hits block of mass 1.0kg placed on a rough horizontal ground and comes out of the block with a velocity of 400m/s. The coefficient of friction between the block and the ground is 0.25. Neglect loss of mass of the block as the bullet pierces through it.
(a) In spite of the fact that friction acts a an external force, can you apply principle of conservation of momentum during interaction of the ullet with the block?
(b) Find velocity of the block immediately after the bullet pierces through it. (c)FInd the distance the block will travel before it stops.
 View Solution
View Solution

