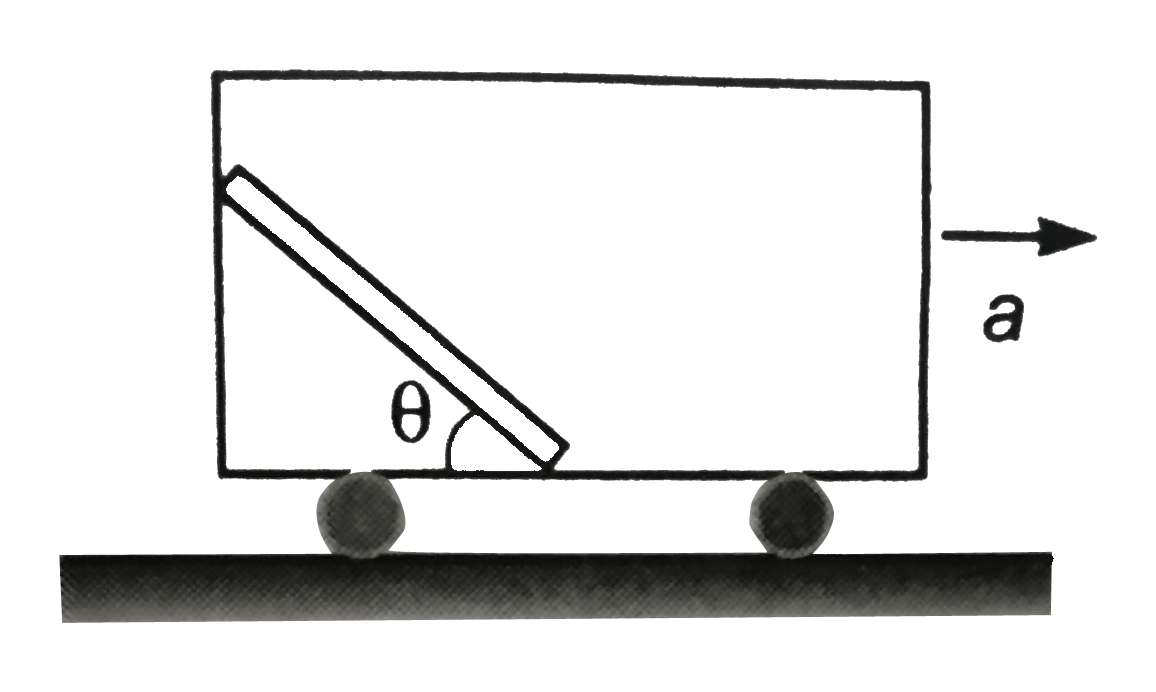
A trolley intially at rest with a solid cylinder placed on its bed such that cylinder axis makes angle $θ$ with direction of motion of trolley as shown in the figure starts to move forward with constant acceleration a. If initial distance of midpoint of cylinder axis from rear edge of trolley bed is $d$ , calculate the distance $s$ which the trolley goes before the cylinder rolls off the edge of its horizontal bed. Assume dimensions of cylinder to be very small in comparision to other dimensions. Neglect slipping.
Calculate als, frictional force acting on the cylinder.

Video Solution

Text Solution

Verified by Experts

Since axis of cylinder is inclined at angle $θ$ with the direction of motion of trolley, therefore components of acceleration a of trolleys, are $a cos θ$ along axis of cylinder and $a sin θ$ norma to axis of the cylinder. Cylinder rolls backward due to this normal component $a sin θ$ .

Due to angular acceleration cylinder axis has acceleration relative trolley bed, which will be equal to $r α$ normal to cylinder axis. But component of accelerations of trolley normal to cylinder axis is $sin θ$ . Therefore, net acceleration of cyinnder axis $(a sin θ - r α)$
normal to axis.
Consider free body diagram of the cylinder as shown in the figure.
$F_{2} = m a sin θ$
$F_{2}$ is not shown in the free body diagram because in this diagram forces acting nromjal to cylinder axis are shown.
For horizontal forces. $F_{1} = m (a sin θ - r α)$ .........i
Taking moment about cyinder axis $F_{1} r = I α$
$I = \frac{m r^{2}}{2} \Rightarrow F_{1} = \frac{1}{2} m r α$ ..............ii
From eqn i and ii $r α = \frac{2}{3} a sin θ$
The cylinder will roll off the edge of trolley bed when its centre of mass reaches the edge. Since, cylinder axis is inclined at an angle $θ$ withdirectionof motion of trolley, therefore, its centre of mass follows a straightline path relative to the trolley bed, and that staightline is normal to cylinder axis. Hence, displacement of centre of mass of the cylinder, relative to trolley is equal to $(d cos e c θ)$ .
Considering motion of cylinder relative to the trolley,
$u = 0$
Acceleration $= r α = \frac{2}{3} a sin θ$
$s = d cos e c θ, t = ?$
Using, $s = u t + \frac{1}{2} a t^{2}, t = \sqrt{\frac{3 d}{a {sin}^{2} θ}}$
Now considering motion of trolley during this interval of time $u = 0$ acceleration =a
$t = \sqrt{\frac{3 d}{a {sin}^{2} θ}, s = ?}$
Using $s = u t + \frac{1}{2} a t^{2}, s = \frac{3}{2} d cos e c^{2} θ$
$F_{1} = \frac{1}{2} m r α = \frac{1}{3} m a sin θ$
total frictional force acting on the cylinder is
$F = \sqrt{F_{1}^{2} + F_{2}^{2}} = \frac{1}{3} m a \sqrt{{sin}^{2} θ + 9 {cos}^{2} θ}$

Updated on:21/07/2023

|

Class 11 PHYSICS RIGID BODY DYNAMICS

Topper's Solved these Questions

Similar Questions

CENGAGE PHYSICS ENGLISH-RIGID BODY DYNAMICS 2-Solved Examples

Home
Ask Doubt
Profile