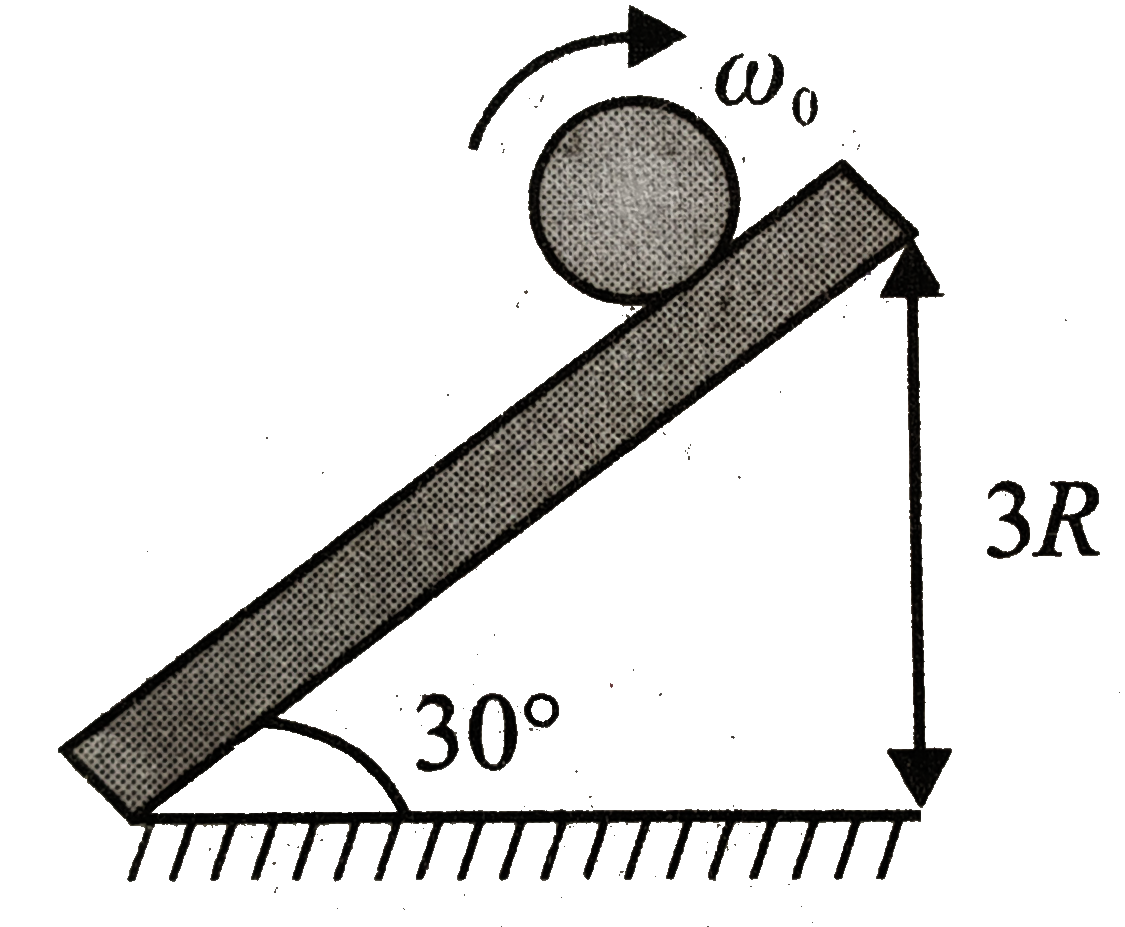
A spinning cylinder with angular velocity $ω_{0}$ of mass $M$ and radius $R$ is lowered on a rough inclined plane of angle $30^{\circ}$ with the horizontal and $μ = 1 / \sqrt{3}$ . The cylinder is released at a height of $3 R$ from horizontal. Find the total time taken by the cylinder to reach the bottom of the incline.

Video Solution

Text Solution

Verified by Experts

The correct Answer is: $\sqrt{\frac{R}{g}}$

We will check whether the clinder slips down the incline or not.
As $m g {sin 30}^{\circ} = μ m g {cos 30}^{\circ}$ , initially the cylinder slips at its place till the agular velocity becomes zero.
$Σ τ = (μ m g cos θ) R = \frac{m R^{2}}{2} α$
$α = \frac{2 μ cos θ}{R} g$
$0 = ω_{0} - α_{1}$ or $t_{1} = \frac{ω_{0}}{α}$

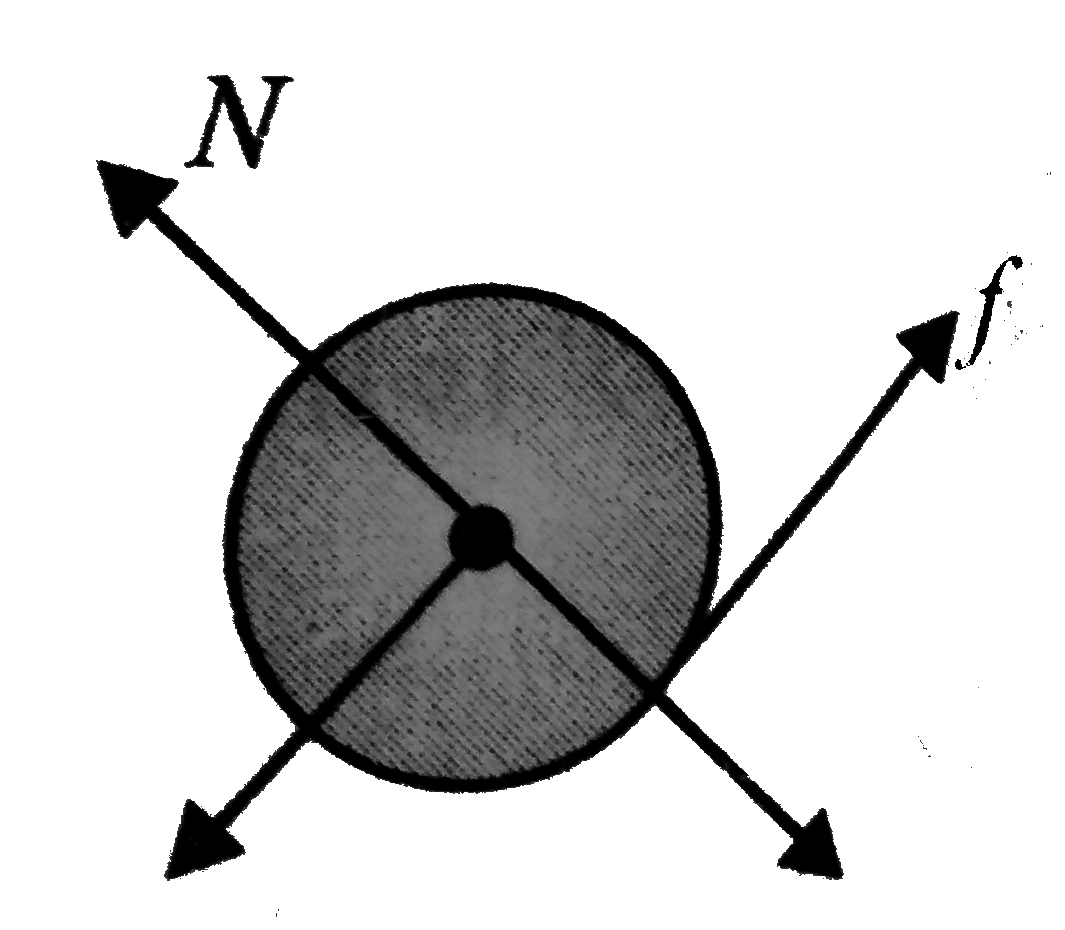
Next the sphere willcome down with the initial angular and linear velocity both being zero.
$fR = \frac{M R^{2}}{2} α, f = \frac{m R α}{2}$
and $m g sin θ - f = m a$
If pure rolling takes place, $R = R α$
$f - m g sin θ - 2 f$ or $f = \frac{1}{3} m g sin θ = \frac{m g}{6}$
As $f_{max} = μ m g cos θ = \frac{1}{\sqrt{3}} = m g \times \frac{\sqrt{3}}{2} = \frac{m g}{2}$
$and f_{max} < f,$ so pure rolling is possible.
$a = \frac{2 F}{m} = \frac{2 - (m g / 6)}{m} = \frac{g}{3}$
Let $t_{2}$ be the time taken to reach the foot of the incline
$\frac{3 R}{{sin 30}^{\circ}} = \frac{1}{2} \frac{g}{3} t_{2}^{2}$ or $t_{2} = 6 \sqrt{\frac{R}{6}}$
Hence, the total time $t = t_{1} + t_{2}$
$= (\frac{ω_{0} R}{g} = g \sqrt{\frac{R}{g}})$

|

Updated on:21/07/2023

Class 11 PHYSICS RIGID BODY DYNAMICS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
A solid cylinder of mass $M$ and radius $R$ rolls without slipping down an inclined plane making an angle $6$ with the horizontal. Then its acceleration is.
A1/3 g sin $θ$
B2/3 g sin $θ$
C2/5 g sin $θ$
D2/7 g sin $θ$

CENGAGE PHYSICS ENGLISH-RIGID BODY DYNAMICS 2-Subjective

Home
Ask Doubt
Profile