A gardener presses the grasscutter with a force F at an angle θ. Assume the motion of grasscutter as pure rolling. Find the:

friction between the grasscutter (assumed as a disc) and ground.
Fsinθ3
Fcosθ3
2F3
2Fcosθ3
The correct Answer is:B
Fcosθ−f=ma …………i
fR=12mR2α⇒fR=12mR2aR
⇒f=ma2………ii
From i and ii
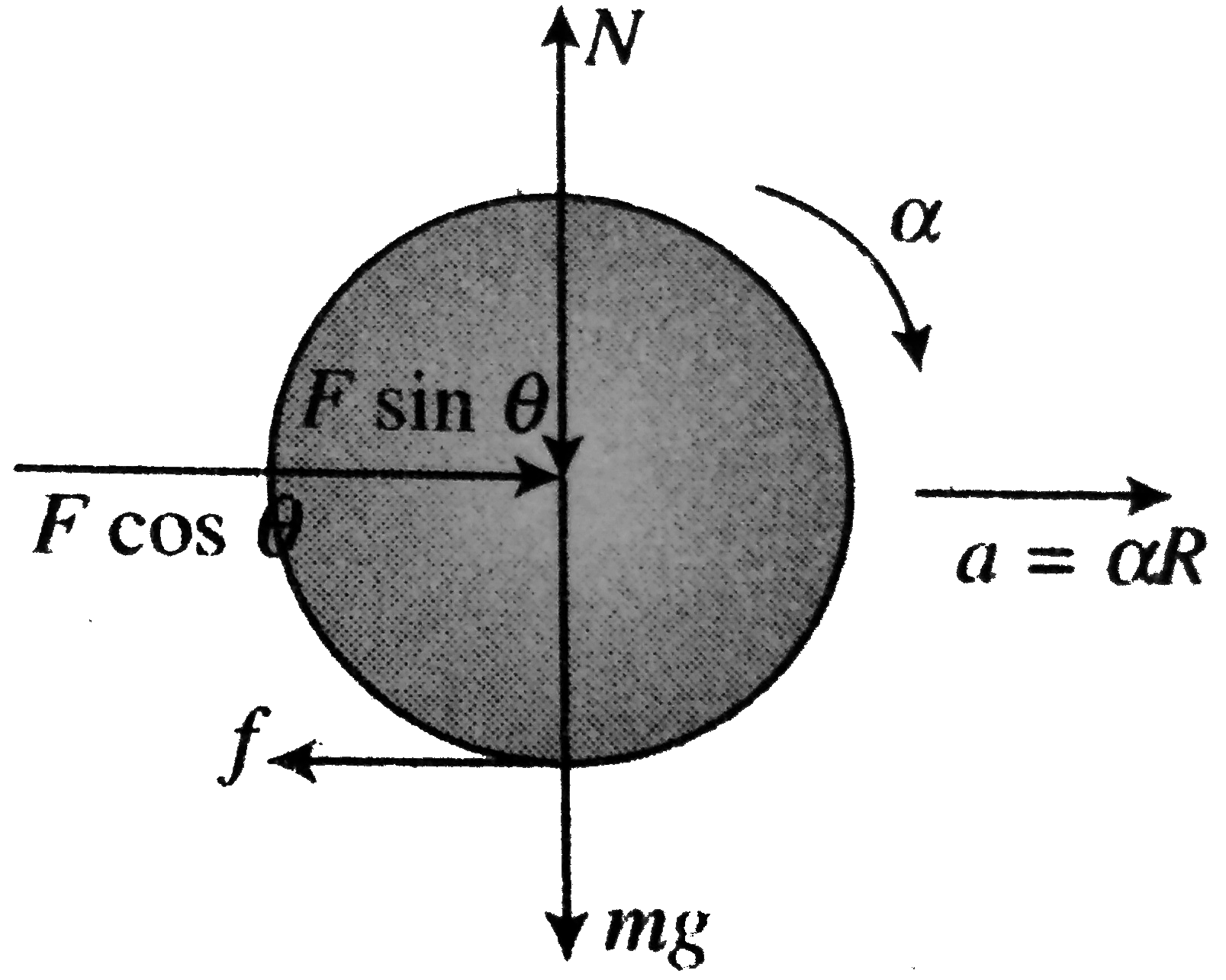
f=Fcosθ3
Now a=2fm=2Fcosθ3m
f≤f1⇒Fcosθ3≤μN
⇒Foscosθ3≤μ(mg+Fsinθ)⇒F≤3μmgcosθ−3μsinθ
Topper's Solved these Questions
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Integer
7 Videos
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Fill In The Blanks
7 Videos
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Multiple Correct
26 Videos
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Integer
11 Videos
- SOUND WAVES AND DOPPLER EFFECTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOUND WAVES AND DOPPLER EFFECTEXERCISE - Integer
16 Videos
Similar Questions
A gardener presses the grasscutter with a force F at an angle θ. Assume the motion of grasscutter as pure rolling. Find the:
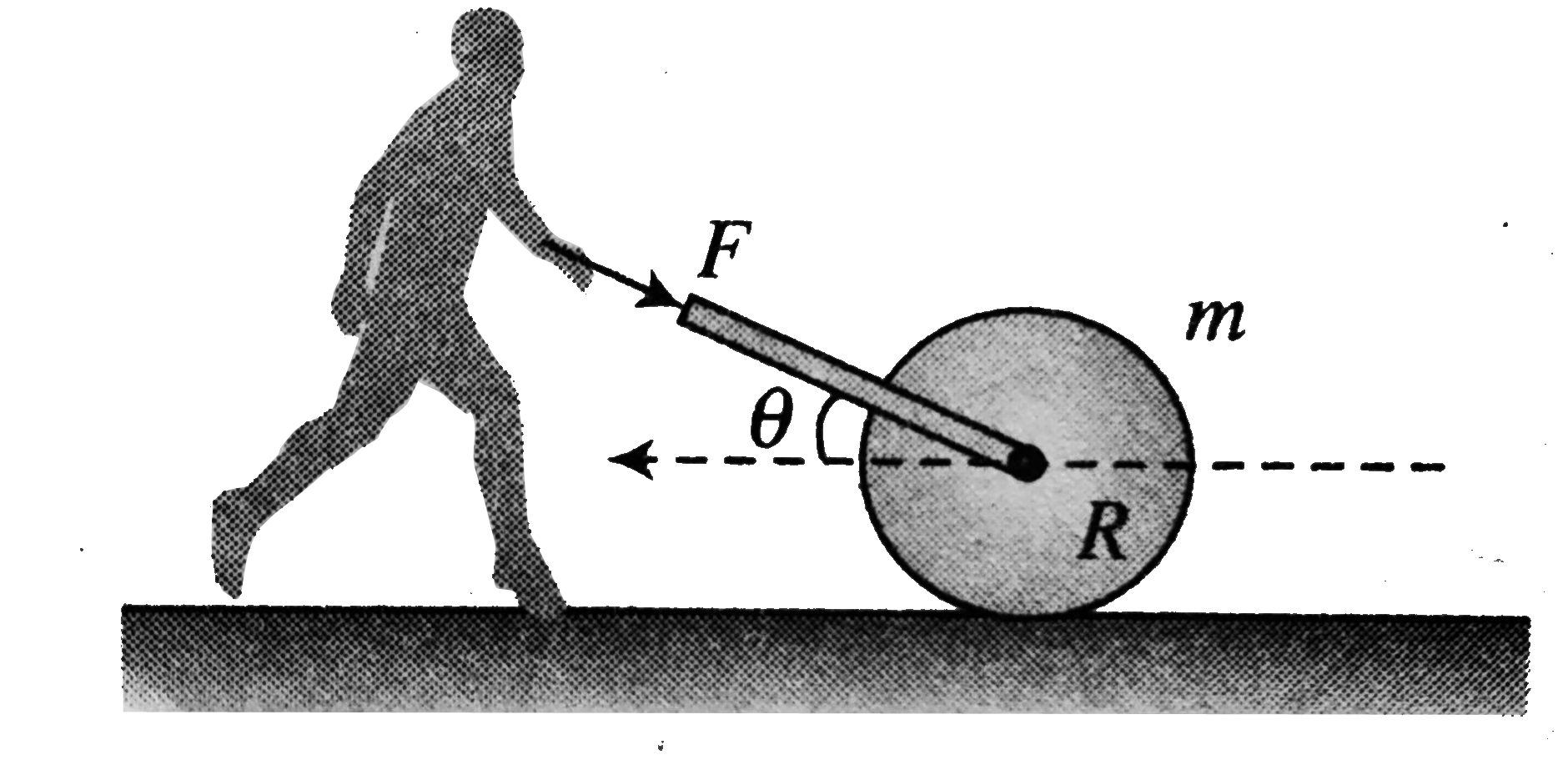
Acceleration of CM of the roller (disc). Assume that the mass of the disc is m and neglect the mass of the connecting rod.
View SolutionA gardener presses the grasscutter with a force F at an angle θ. Assume the motion of grasscutter as pure rolling. Find the:
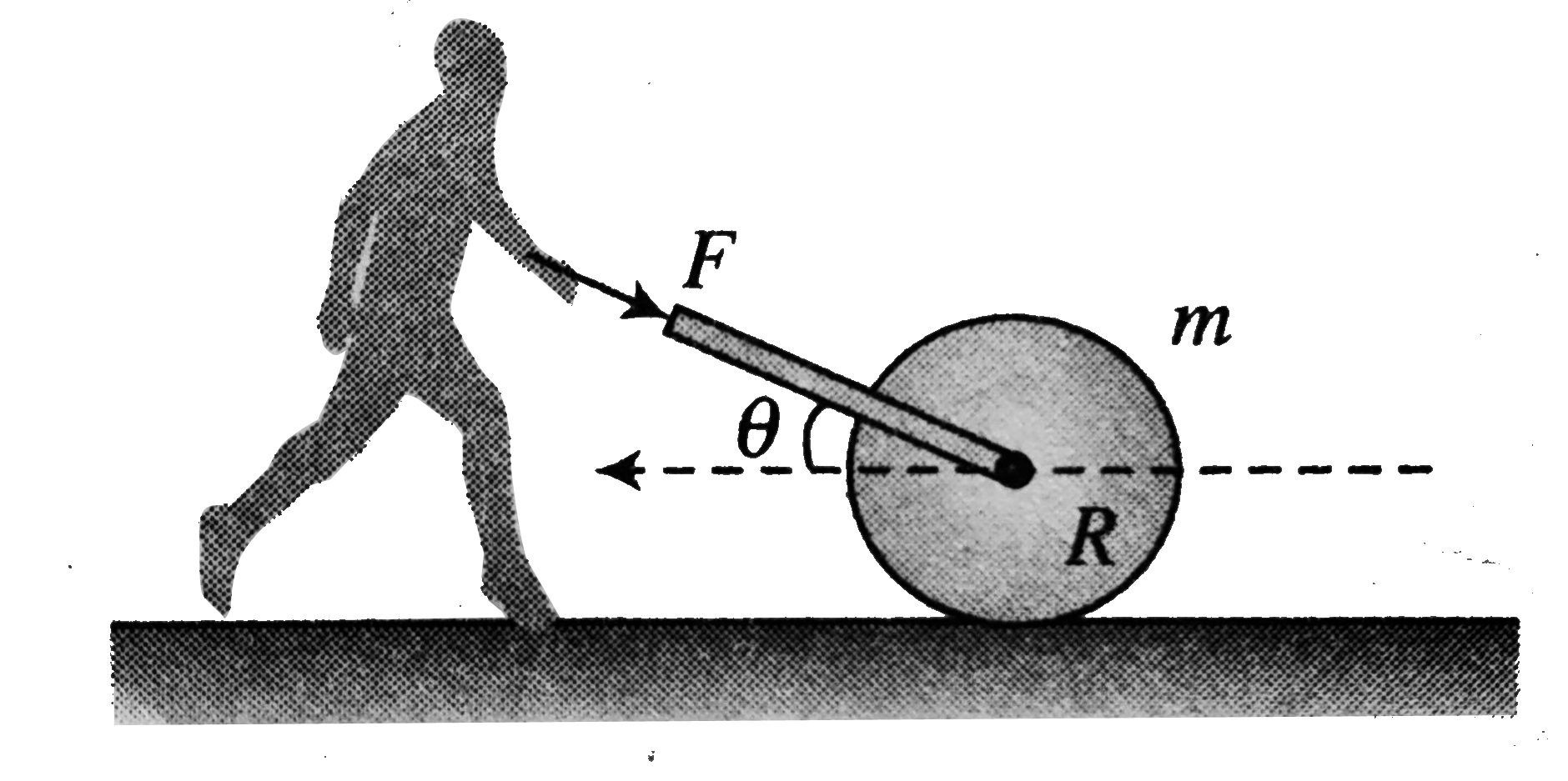
Maximum force F for no relative slidng if th coeficient of friction between the roller and ground is μ
View Solution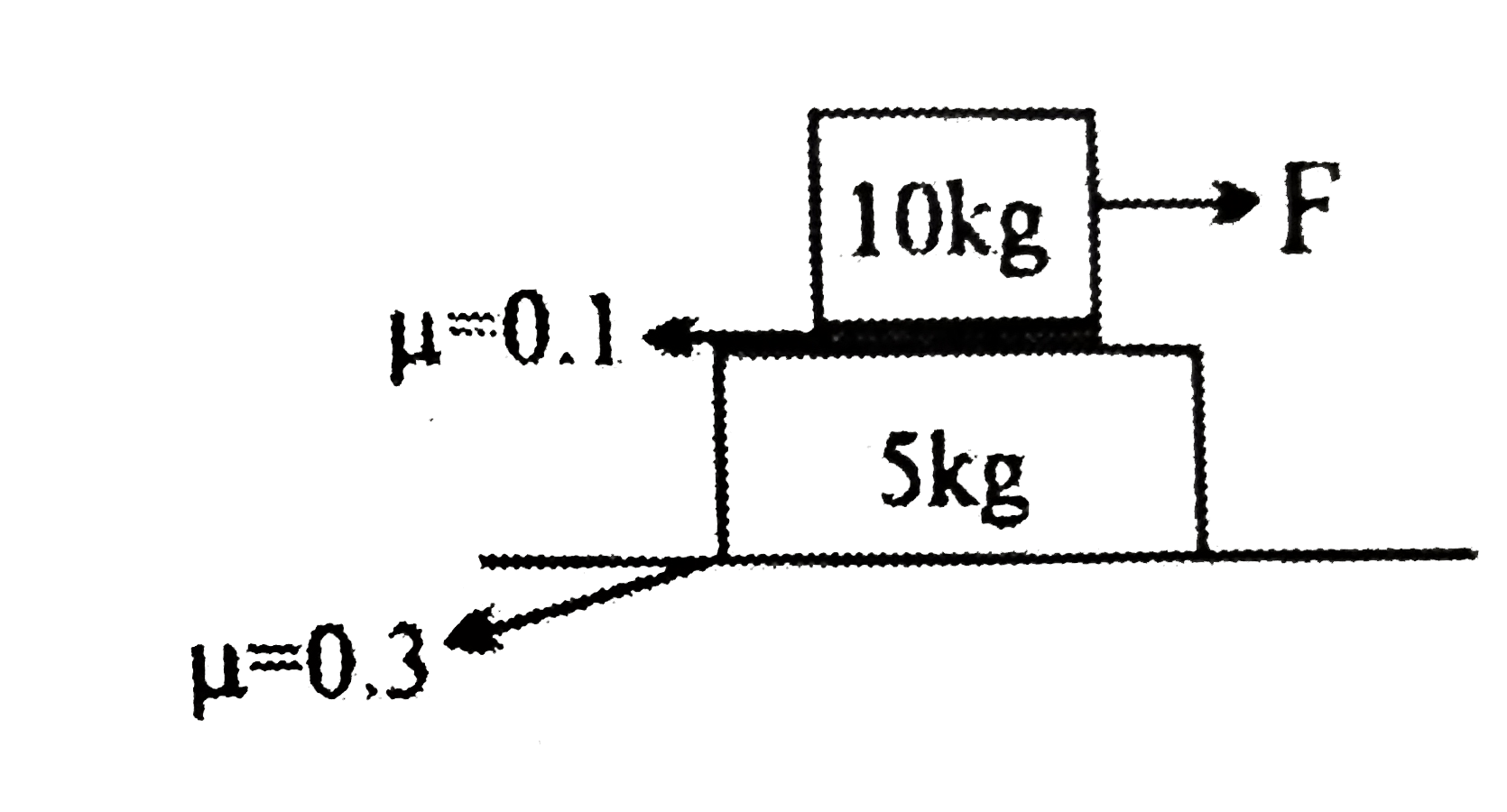
When F = 2N, the frictional force between 5 kg block and ground is
View SolutionA stick o fmas density λ=8kg/m rests on a disc of radius R=20cm as shown in the figure. The stick makes an angle θ=37∘ with the horizontal and is tangent to the disc at its upper end. Friction exists at all point of contact and assume that it is large enough to keep the system at rest. Find the friction force (in Newton) between the ground and the disc. (take g=10m/s2)

View SolutionA block of mass m is pressed against a wall which is moving with an acceleration a as shown in figure If the block is pulled at an angle θ with downward vertical by a force F and it does not slide relative to the wall . Find the
a. friction force between the block and wall
b.inimum magnitude of F so as to cayse a relative sliding between the block and wall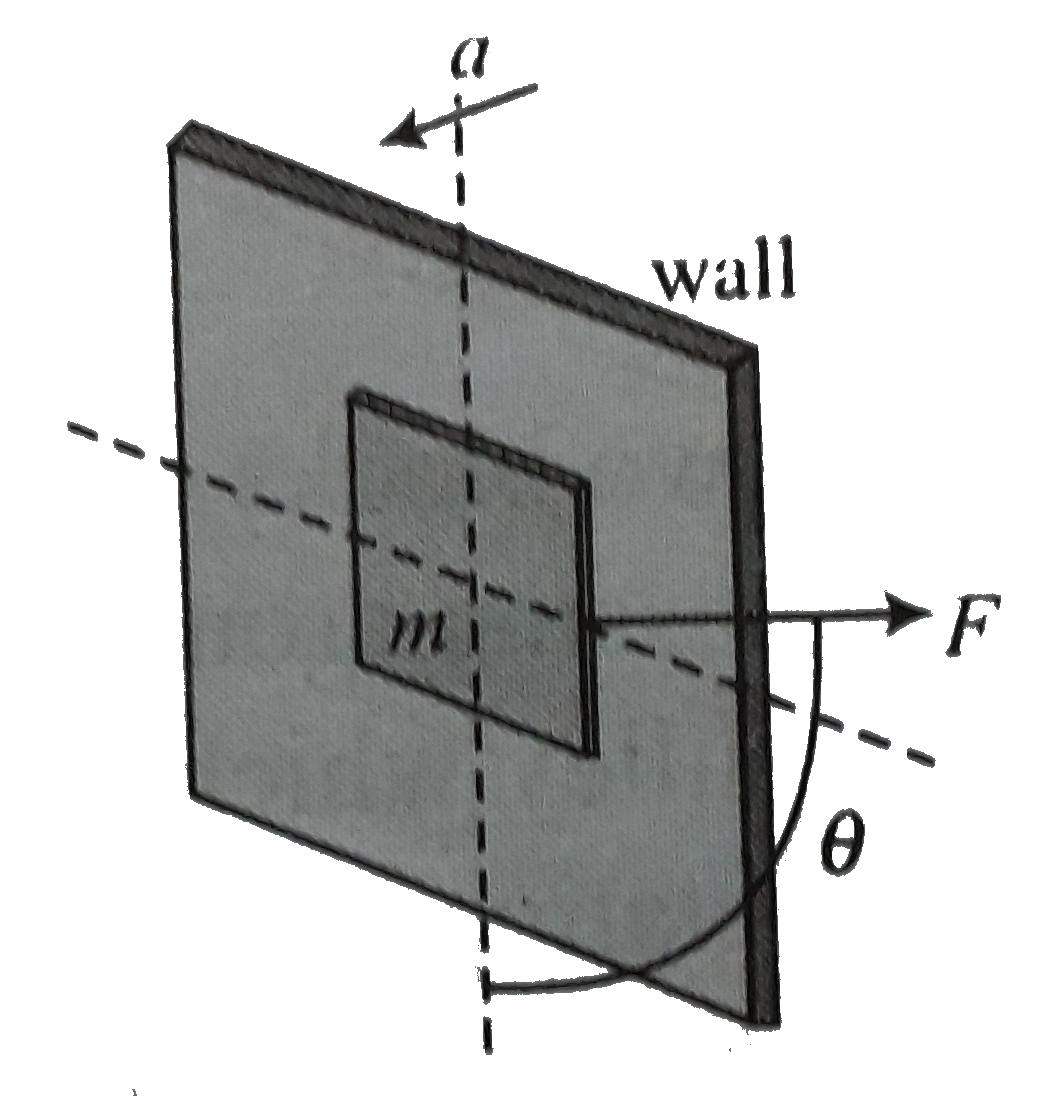
View SolutionA uniform ring of mass 'm' and radius 'R' is projected horizontally with velcoty v0 on a rough horizontal floor, so that it starts off with a purely sliding motion and it acquires a pure rolling motion after moving a distance d. If the coefficient of friction between the ground and ring is μ, then work done by the friction in the process is
View SolutionA disc of radius R and mass M is under pure rolling under the action of a force F applied at the topmost point as shown in figure. There is sufficient friciton between the disc and the horizontal surface. The acceleration is given as

View SolutionA uniform disc is acted by two equal forces of magnitude F. One of them, acts tangentially to the disc, while other one is acting at the central point of the disc. The friction between disc surface and ground surface in nF. If r be the radius of the disc, then the value of n would be (in N)
View Solutionfind the resultant of two forces each having magnitude F0 and angle between them is θ.
View SolutionAn aeroplane requires a speed of 72 kmph for a take off with 150m run on the ground. The mass of the plane is 1500kg and the coefficient of friction between the aeroplane and the ground is 0.4. Assuming that the aeroplane acceleration uniformly during take off, find the minimum force exerted by the engine of the aeroplane for take off.
View Solution
