A rocket ejects the fuel (hot gases) of density ρ from the chamber which is maintained at a pressure P1, say. The atmospheric pressure is P0. If the base area of the cylindrical chamber is A1 and the area of the hole through which hot gases escape from the rocket is A2 find (a) velocity of efflux of the fuel, (b) thrust exerted on the rocket given by the escaping fuel.
The correct Answer is:(P−P0)
To solve the problem step by step, we will break it down into two parts: (a) finding the velocity of efflux of the fuel and (b) calculating the thrust exerted on the rocket.
Part (a): Velocity of Efflux of the Fuel
1. Understanding the System:
We have a cylindrical chamber with base area A1 and a hole with area A2 through which the fuel (hot gases) is ejected. The pressure inside the chamber is P1 and the atmospheric pressure outside is P0.
2. Applying the Continuity Equation:
The volume flow rate must be conserved. Therefore, we can write:
A1V1=A2V2
where V1 is the velocity of the fluid inside the chamber and V2 is the velocity of the fluid as it exits through the hole.
3. Applying Bernoulli's Equation:
According to Bernoulli's theorem, we can relate the pressures and velocities at two points (inside the chamber and at the exit). We can express this as:
P1+12ρV21=P0+12ρV22
Rearranging gives:
P1−P0=12ρV22−12ρV21
This simplifies to:
P1−P0=ρ2(V22−V21)
4. Assuming V1 is Small:
If the hole area A2 is much smaller than the base area A1, we can assume that V1 is much smaller than V2 (i.e., V1≈0). Thus, the equation simplifies to:
P1−P0=ρ2V22
5. Solving for V2:
Rearranging the equation gives:
V22=2(P1−P0)ρ
Taking the square root:
V2=√2(P1−P0)ρ
Part (b): Thrust Exerted on the Rocket
1. Understanding Thrust:
The thrust F exerted on the rocket is due to the change in momentum of the escaping fuel. It can be expressed as:
F=(mass flow rate)×V2
2. Calculating Mass Flow Rate:
The mass flow rate ˙m can be calculated using the density and the volume flow rate:
˙m=ρ⋅(volume flow rate)=ρA2V2
3. Substituting into the Thrust Equation:
Therefore, the thrust can be expressed as:
F=˙m⋅V2=(ρA2V2)V2=ρA2V22
4. Substituting V2:
Now substituting V22 from part (a):
F=ρA2(2(P1−P0)ρ)=2A2(P1−P0)
Final Answers
- (a) The velocity of efflux of the fuel is:
V2=√2(P1−P0)ρ
- (b) The thrust exerted on the rocket is:
F=2A2(P1−P0)
We have a cylindrical chamber with base area A1 and a hole with area A2 through which the fuel (hot gases) is ejected. The pressure inside the chamber is P1 and the atmospheric pressure outside is P0.
The volume flow rate must be conserved. Therefore, we can write:
A1V1=A2V2
where V1 is the velocity of the fluid inside the chamber and V2 is the velocity of the fluid as it exits through the hole.
According to Bernoulli's theorem, we can relate the pressures and velocities at two points (inside the chamber and at the exit). We can express this as:
P1+12ρV21=P0+12ρV22
Rearranging gives:
P1−P0=12ρV22−12ρV21
This simplifies to:
P1−P0=ρ2(V22−V21)
If the hole area A2 is much smaller than the base area A1, we can assume that V1 is much smaller than V2 (i.e., V1≈0). Thus, the equation simplifies to:
P1−P0=ρ2V22
Rearranging the equation gives:
V22=2(P1−P0)ρ
Taking the square root:
V2=√2(P1−P0)ρ
The thrust F exerted on the rocket is due to the change in momentum of the escaping fuel. It can be expressed as:
F=(mass flow rate)×V2
The mass flow rate ˙m can be calculated using the density and the volume flow rate:
˙m=ρ⋅(volume flow rate)=ρA2V2
Therefore, the thrust can be expressed as:
F=˙m⋅V2=(ρA2V2)V2=ρA2V22
Now substituting V22 from part (a):
F=ρA2(2(P1−P0)ρ)=2A2(P1−P0)
- (a) The velocity of efflux of the fuel is:
V2=√2(P1−P0)ρ
- (b) The thrust exerted on the rocket is:
F=2A2(P1−P0)
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Single Correct95videos
FLUID MECHANICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Multipe Correct15videos
FLUID MECHANICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Exercise 4.410videos
FLUID MECHANICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Integer2videos
DIMENSIONS & MEASUREMENT
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GRAVITATIONEXERCISE - INTEGER_TYPE1videos
GRAVITATION
Similar Questions
In a rocket, fuel burns at the rate of 2 kg/s. This fuel gets ejected from the rocket with a velocity of 80 km/s. Force exerted on the rocket is -
View SolutionIn a rocket, fuel burns at the rate of 2 kg/s. This fuel gets ejected from the rocket with a velocity of 80 km/s. Force exerted on the rocket is -
View SolutionThe pressure of the gas in a cylindrical chamber is p0. The vertical force exerted by the gas on its hemispherical end is
 View Solution
View SolutionIn a rocket, fuel bums at the rate of 1 kg/s. This fuel is ejected from the rocket with a velocity of 60 km/s. This exerts a force on the rocket equal to
View SolutionIf velocity of efflux is v and area of orifice is A0 then
 View Solution
View SolutionIn the figure shown the velocity and pressure of the liquid at the cross section (2) are given by (If P0 is the atmospheric pressure).
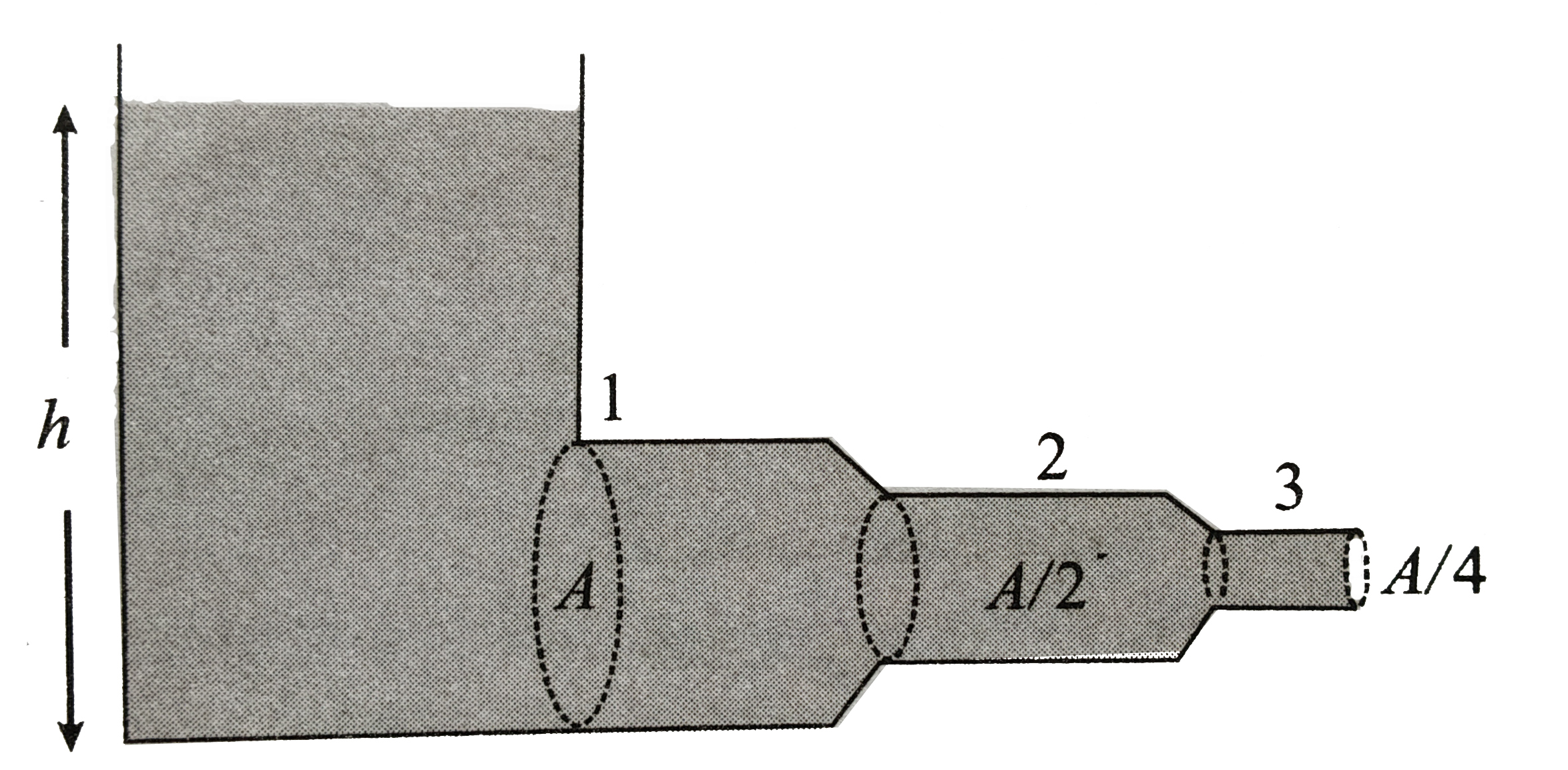 View Solution
View SolutionA diwali rocket is ejecting 0.05kg of gases per second at a velocity of 400m/sec. The accelerating force on the rocket is
View SolutionWhich of the following is used as rocket fuel?
View SolutionA rocket burns 50g of fuel per second ejecting it as a gas with a velocity of 5×10cms−1. What force is exerted by the gas on the rocket?
View SolutionA rocket is launched vertical from the surface of the earth of radius R with an initial speed v. If atmospheric resistance is neglected, then maximum height attained by the rocket is
View Solution

