An open tank 10m long and 2m deep is filled up to 1.5m height of oil of specific gravity 0.82. The tank is uniformly accelerated along its length from rest to a speed of 20m/s horizontally. The shortest time in which the speed may be attained without spilling any oil is
20s
18s
10s
5s
The correct Answer is:A
To solve the problem, we need to determine the shortest time in which the tank can accelerate to a speed of 20 m/s without spilling any oil. Here’s a step-by-step solution:
Step 1: Understand the problem
We have an open tank that is 10 m long and 2 m deep, filled with oil to a height of 1.5 m. The specific gravity of the oil is 0.82. The tank is accelerated horizontally, and we need to find the time it takes to reach a speed of 20 m/s without spilling the oil.
Step 2: Calculate the density of the oil
The specific gravity (SG) of the oil is given as 0.82. The density of water is approximately 1000 kg/m³. Therefore, the density of the oil (ρ_oil) can be calculated as:
ρoil=SG×ρwater=0.82×1000kg/m3=820kg/m3
Step 3: Determine the angle of the oil surface due to acceleration
When the tank accelerates, the oil surface will tilt. The angle (θ) can be determined using the relationship between the acceleration (a) of the tank and the gravitational acceleration (g = 9.81 m/s²):
tan(θ)=ag
Step 4: Relate the tilt of the oil surface to the height difference
The height difference (h) across the length of the tank (10 m) can be expressed as:
h=L⋅tan(θ)=10⋅tan(θ)
Substituting for tan(θ):
h=10⋅ag
Step 5: Calculate the maximum height difference before spilling
To avoid spilling, the height of the oil must not exceed the tank's height of 1.5 m. Therefore:
h≤1.5m
Substituting for h:
10⋅ag≤1.5
ag≤0.15
a≤0.15⋅g=0.15⋅9.81≈1.4715m/s2
Step 6: Calculate the required acceleration to reach 20 m/s
Using the first equation of motion:
v=u+at
Where:
- v = final velocity = 20 m/s
- u = initial velocity = 0 m/s
- a = acceleration
- t = time
Rearranging gives:
t=v−ua=20a
Step 7: Substitute the maximum acceleration
Substituting the maximum acceleration we found:
t=201.4715≈13.59s
Conclusion
The shortest time in which the speed may be attained without spilling any oil is approximately 13.59 seconds.
---
We have an open tank that is 10 m long and 2 m deep, filled with oil to a height of 1.5 m. The specific gravity of the oil is 0.82. The tank is accelerated horizontally, and we need to find the time it takes to reach a speed of 20 m/s without spilling the oil.
The specific gravity (SG) of the oil is given as 0.82. The density of water is approximately 1000 kg/m³. Therefore, the density of the oil (ρ_oil) can be calculated as:
ρoil=SG×ρwater=0.82×1000kg/m3=820kg/m3
When the tank accelerates, the oil surface will tilt. The angle (θ) can be determined using the relationship between the acceleration (a) of the tank and the gravitational acceleration (g = 9.81 m/s²):
tan(θ)=ag
The height difference (h) across the length of the tank (10 m) can be expressed as:
h=L⋅tan(θ)=10⋅tan(θ)
Substituting for tan(θ):
h=10⋅ag
To avoid spilling, the height of the oil must not exceed the tank's height of 1.5 m. Therefore:
h≤1.5m
Substituting for h:
10⋅ag≤1.5
ag≤0.15
a≤0.15⋅g=0.15⋅9.81≈1.4715m/s2
Using the first equation of motion:
v=u+at
Where:
- v = final velocity = 20 m/s
- u = initial velocity = 0 m/s
- a = acceleration
- t = time
t=v−ua=20a
Substituting the maximum acceleration we found:
t=201.4715≈13.59s
The shortest time in which the speed may be attained without spilling any oil is approximately 13.59 seconds.
Topper's Solved these Questions
- FLUID MECHANICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Multipe Correct
15 Videos
- FLUID MECHANICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Assertion-Reasoning
8 Videos
- FLUID MECHANICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Subjective
25 Videos
- DIMENSIONS & MEASUREMENTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Integer
2 Videos
- GRAVITATIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GRAVITATIONEXERCISE - INTEGER_TYPE
1 Videos
Similar Questions
A block of mass 10 kg accelerates uniformly from rest to a speed of 2 m/s in 20 sec. The average power developed in time interval of 0 to 20 sec is
View SolutionA closed rectangular tank 10m long, 5m wide and 3m deep is completely filled with an oil of specific gravity 0.92. Find the pressure difference between the rear and front corners of the tank, if it is moving with an acceleration of 3m/s2 in the horizontal direction.
View Solution
Knowledge Check
A car accelerates by 50 m//s^(2). It would, attain a speed of 100 km per hour from rest in
A0.28 sB0.56 sC1.12 sD2.00 s
A ball is thrown at a speed of 20 m/s at an angle of 30∘ with the horizontal . The maximum height reached by the ball is
(Use g=10m/s2)
View SolutionA spherical tank of 1.2m radius is half filled with oil of relative density 0.8. If the tank is given a horizontal acceleration of 10m/s2, the maximum pressure on the tank is √2P pascal. Find the value of P.
View SolutionA particle is projected at an angle 60∘ with horizontal with a speed v=20m/s. Taking g=10m/s2. Find the time after which the speed of the particle remains half of its initial speed.
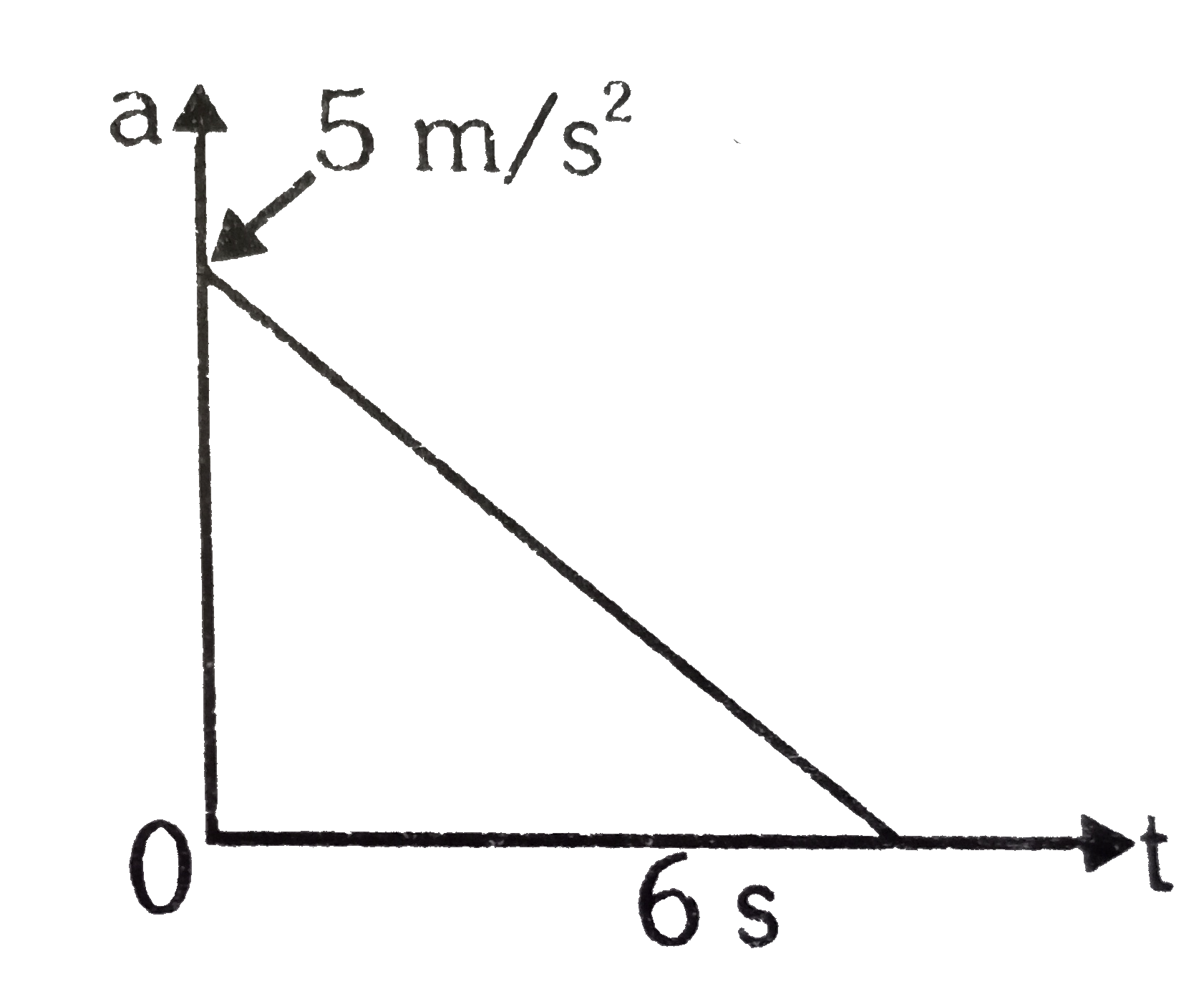
View SolutionA particle starts from rest. Its acceleration at time t=0 is 5m/s2 which varies with time as shown in the figure. The maximum speed of the particle will be
View SolutionA tank 30 m long. 24 m wide and 4.5 m deep is to be made. It is open from the top. Find the cost of iron- sheet required at the rate of rupes 65 per m2. To make the tank.
View SolutionA car moving on a straight road accelerates from a speed of 4.1 m/s to a speed of 6.9 m/s in 5.0 s. What was its average acceleration?
View SolutionA ball is thrown up at a speed of 4.0 m/s. Find the maximum height reached by the ball. Take g=10m/s2.
View Solution
