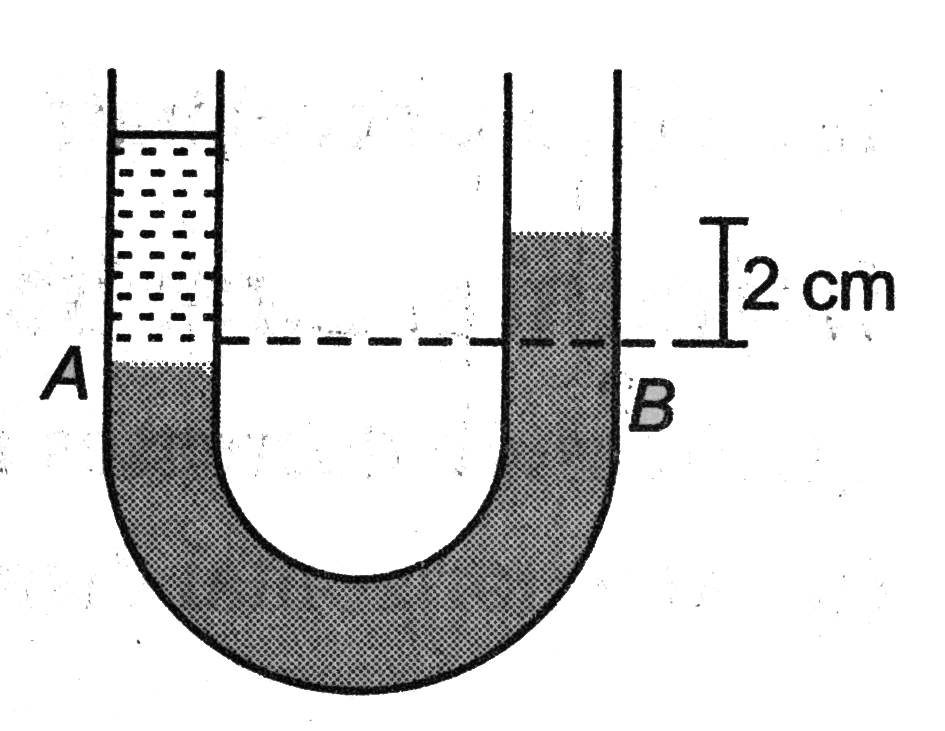
The liquids shown in figure in the two arms are mercury (specific gravity=13.6) and water. If the difference of heights of the mercury columns is 2 cm. Find the height h of the water column.
 .
.
6.8cm
13.6cm
27.2cm
54cm
The correct Answer is:C
h×1000×g=2100×13600×g
or h=2×13.6100m=27.2cm
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Multipe Correct15videos
FLUID MECHANICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Assertion-Reasoning8videos
FLUID MECHANICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Subjective25videos
FLUID MECHANICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Integer2videos
DIMENSIONS & MEASUREMENT
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GRAVITATIONEXERCISE - INTEGER_TYPE1videos
GRAVITATION
Similar Questions
The liquids shown in figure in the two arms are mercury (specific gravity =13.6) and water. If the difference of heights of the mercury columns is 2 cm, find the height of the water column.
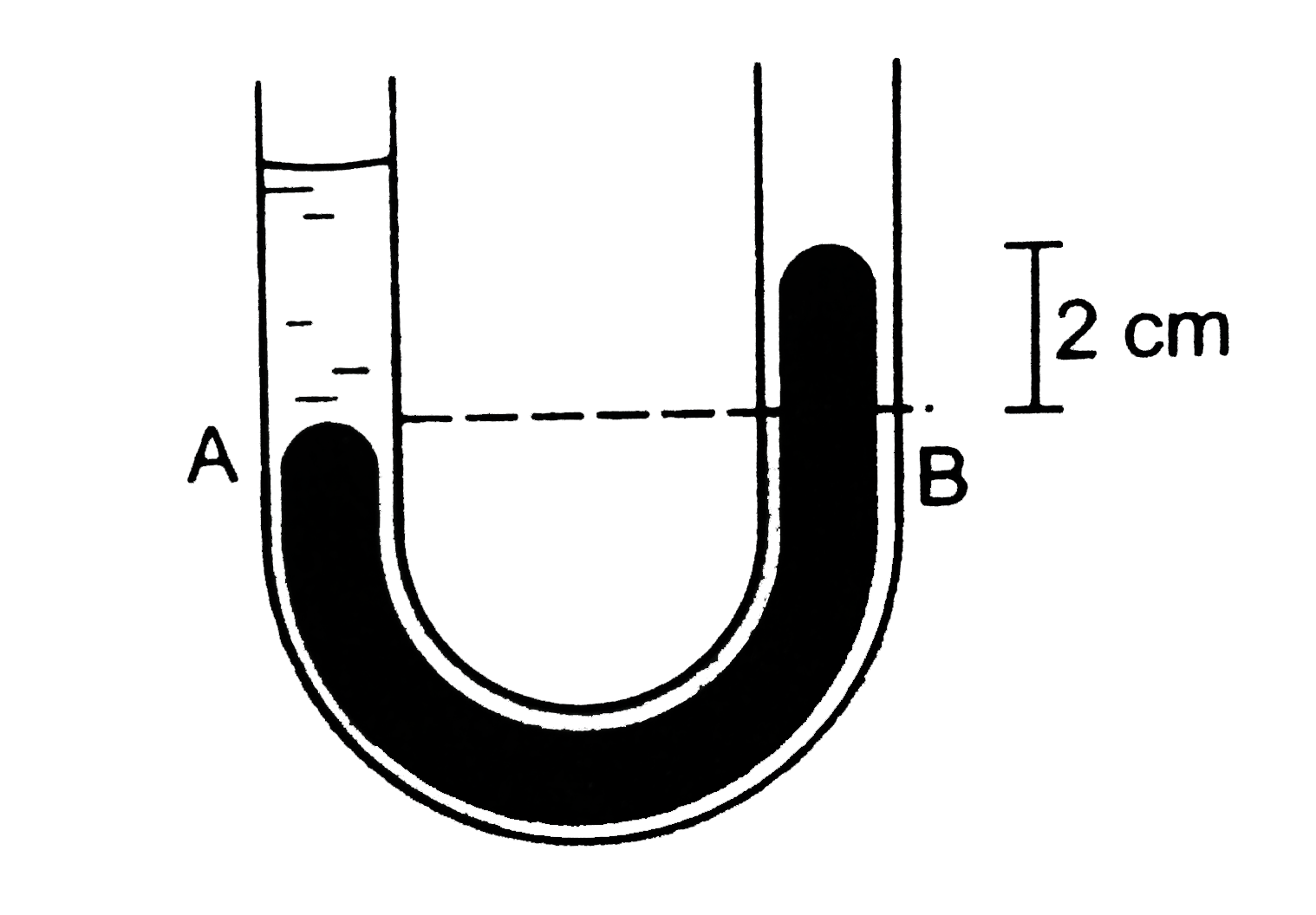 ,View Solution
,View SolutionThe liquids shown in figure in the two arms are mercury (specific gravity =13.6) and water. If the difference of heights of the mercury columns is 2 cm, find the height of the water column.
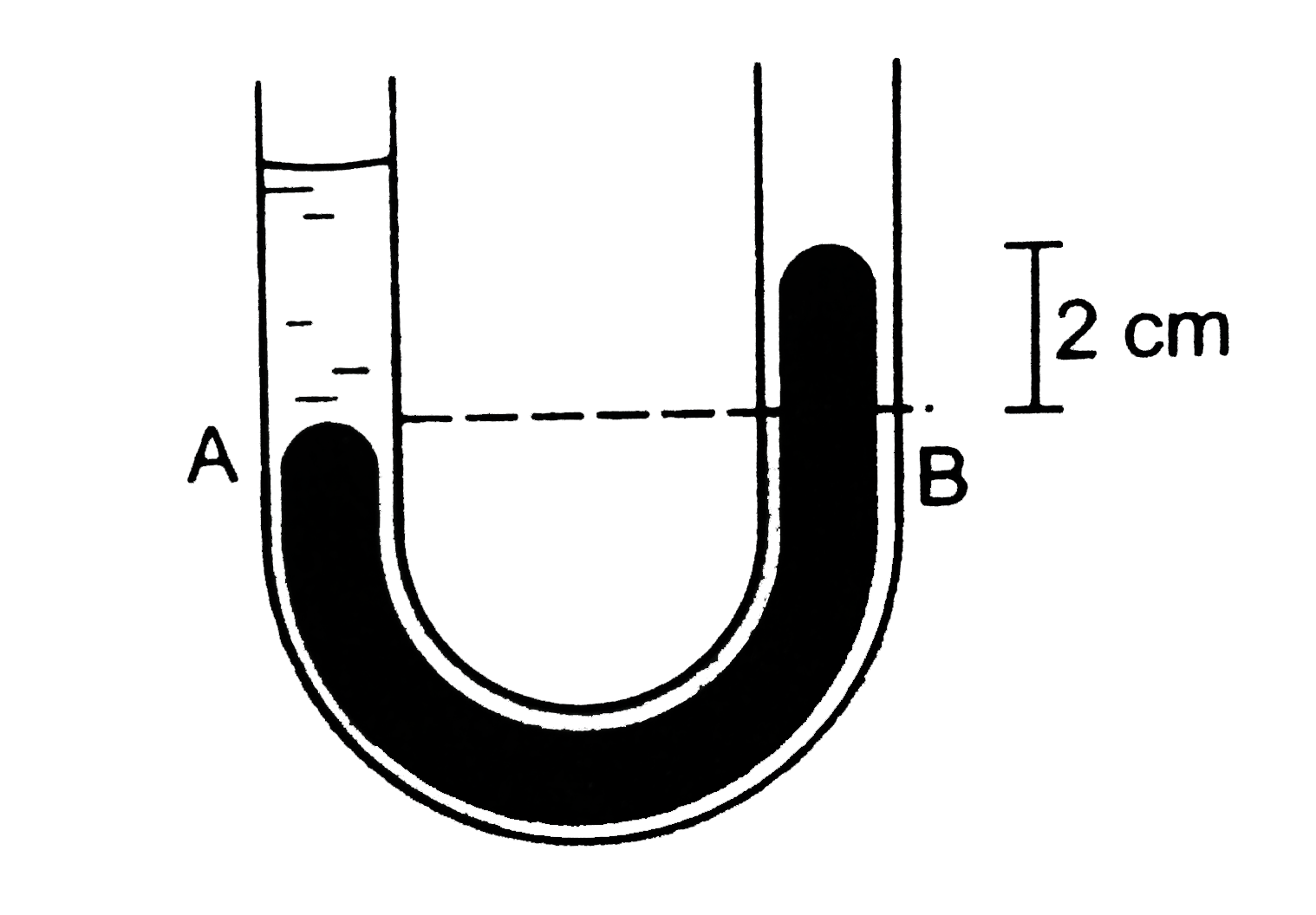 ,View Solution
,View SolutionExpress one atm pressure in terms of the height of mercury column.
View SolutionWill the height of the water column change if the cross section of the water column is made wider ?
View SolutionA cone of a radius 5 cm is filled with water. If the water poured in a cylinder of radius 10cm, the height of the water rises 2 cm, find the height of the cone.
View SolutionA cone of a radius 5cm is filled with water. If the water poured in a cylinder of radius 10cm, the height of the water rises 2cm, find the height of the cone.
View SolutionWater and oil are poured into the two limbs of a U-tube containig mercury. The interface of the mercury and the liquids are at the same height in both limbs.
Determine the height of the water columnh1 if that of the oil h2=20cm. The density of the oil is 0.9.
 .View Solution
.View SolutionMercury of density ρm is poured into cylinderical communicating vessels of cross-sectional area 2A and A respectively. A solid iron cube of volume V0 and relative density 2 is dropped into the broad vessel, and as a result the level of the mercury in it rises. Then, water is poured into the broader vessel until the mercury reaches the previous level in it. Find the height of water column if it does not submerge the block.
View SolutionBy taking two J- tubes at constant temperature what is the difference in the levels of mercury in two columns ?
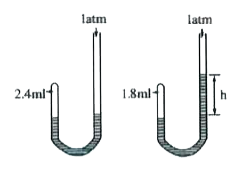 View Solution
View Solution(a) Calculate the height of a water column which will exert on its base the same pressure as the 70 cm column of mercury. Density of mercury is 13.6gcm−3
(b) Will the height of the water column in part (a) change if the cross section of the water column is made wider ?View Solution

