A non-uniform cylinder of mass m, length l and radius r is having its centre of mass at a distance l.4 from the centre and lying on the axis of the cylinder. The cylinder is kept in a liquid of uniform density ρ. The moment of inertia of the rod about the centre of mass is l. The angular acceleration of point A relative to point B just after the rod is released from the position as shown in the figure is

(a)πρgl2r2I
(b)πρgl2r24I
(c)πρgl2r22I
(d)3πρgl2r24I
The correct Answer is:B
Torque about CM 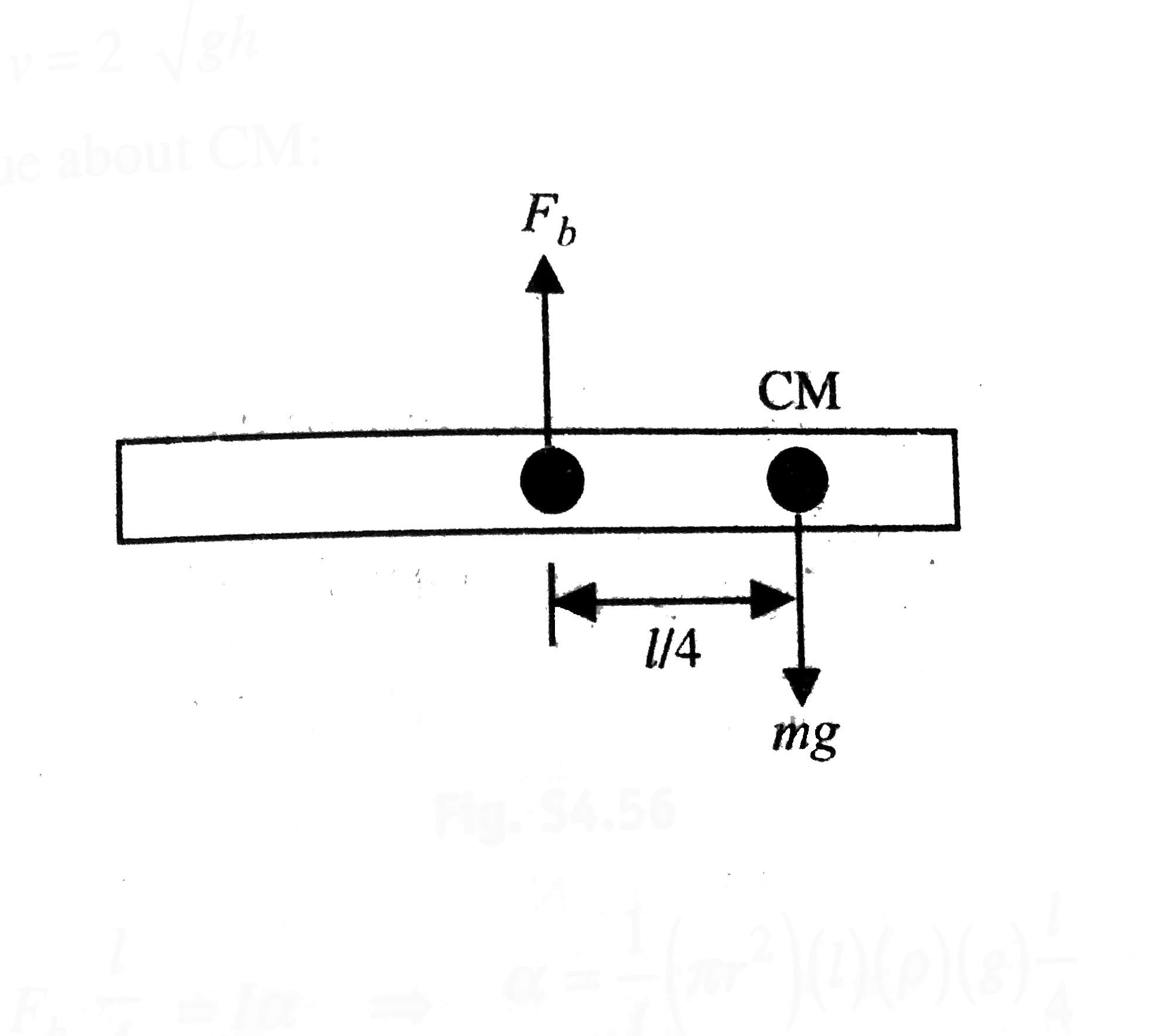
Fbl4=Iα⇒α=1I(πr2)(l)(ρ)(g)l4
⇒α=πr2l2gρ4I
Topper's Solved these Questions
- FLUID MECHANICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Multipe Correct
15 Videos
- FLUID MECHANICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Assertion-Reasoning
8 Videos
- FLUID MECHANICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Subjective
25 Videos
- DIMENSIONS & MEASUREMENTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Integer
2 Videos
- GRAVITATIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GRAVITATIONEXERCISE - INTEGER_TYPE
1 Videos
Similar Questions
A non-uniform rod of mass m, length l and radius r is having its centre of mass at a distance l/4 from the centre and lying on the axis of the cylinder. The cylinder is kept in a liquid of uniform density ρ. The moment of inertia of the rod about the centre of mass is I. The angular acceleration of point A relative to point B just after the rod is released from the position as shown in the figure is

View SolutionA non uniform cylinder of mass m, length l and radius r having its C.O.M at a distance l4 from centre and lying on axis of cylinder . The cylinder is kept in a liquid of unifrom density ρ. The moment of inertia of the rod about C.O.M is I. The angular acceleration of point A relative to point B just after the rod is released from position shown in figure is .

View SolutionA thin wire of length L and uniform linear mass density ρ is bent into a circular loop with centre at O as shown. The moment of inertia of the loop about the axis XX' is
View SolutionThe mass of the cylinder is 25 kg and radius of cylinder is 5 m. Find the moment of inertia of a solid cylinder about a tangent to the cylinder.
View SolutionA cylinder of mass m and radius R is kept on a rough surface after giving its centre a horizontal speed v0. Find the speed of the centre of the cylinder when it stops slipping.
View Solution
Find the moment of inertia of the rod AB about an axis yy as shown in figure. Mass of the rod is m and length is l.
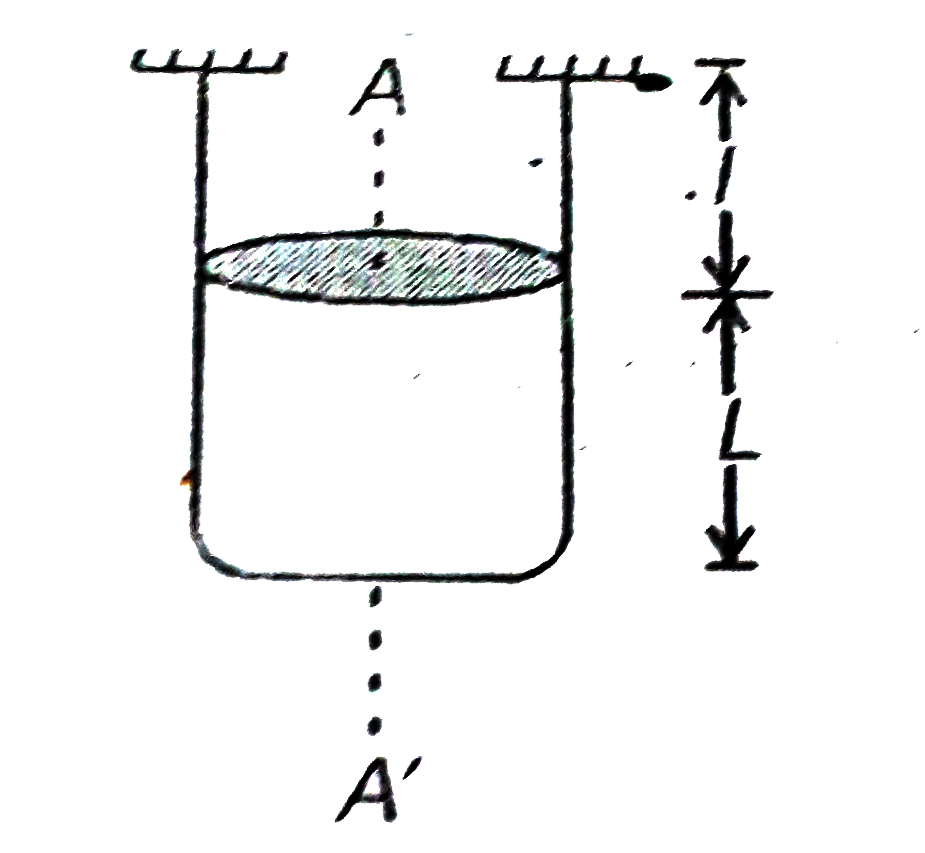
View SolutionA solid cylinder of mass m length L and radius R is suspended by means of two ropes of length l each as shown. Find the time period of small angular oscillations of the cylinder about its axis AA'
View SolutionA body has mass M and radius 2r. If the body assumes four shapes, solid cylinder, solid sphere, disc and ring of same radius, then the moment of inertia will be maximum about axis through centre of mass for:
View SolutionMoment of inertia of a cylinder of mass M, length L and radius R about an axis passing through its centre and perpendicular to the axis of the cylinder is I=M(R24+L212). If such a cylinder is to be made for a given mass of a material, the ratio L/R for it to have minimum possible I is :
View SolutionThe radius of gyration of a uniform rod of length L about an axis passing through its centre of mass is
View Solution
