A horizontal force of magnitude Facts at the end P of a uniform rigid rod which is welded at point Q. In each case 1 and 2, as shown in Fig., find the reaction. force acting at a point C at a distance x from the fixed end Q of the rod.
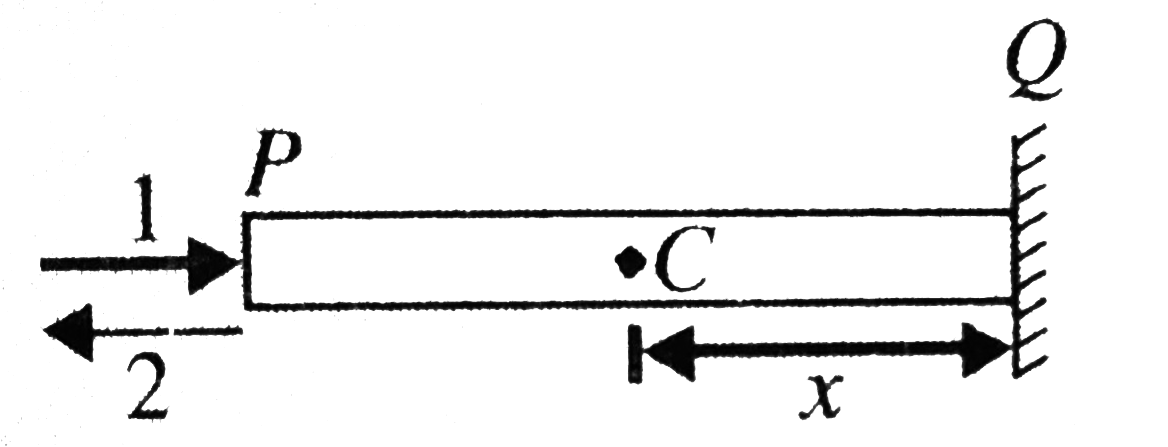
Since the shaded segment is in translational equilibrium at rest
∑F=|F−F|=0 in both the figures
This givs F'=F.

Since the rod is in rotational equilibrium
∑τ=F'x−Fl=0
This gives F'=Flx
Compresive forces compres the rod tensile forces elongate the rod and shearing forces twise (bend) the rod. The tensile and compresive forces are equal to the applied force when the rod is in eqilibrium horizontally. Whereas the shearing force need be equal to the applied force.
Topper's Solved these Questions
- PROPERTIES OF SOLIDS AND FLUIDSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - Exercise 5.2
6 Videos
- PROPERTIES OF SOLIDS AND FLUIDSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - Exercise 5.3
9 Videos
- PROPERTIES OF SOLIDS AND FLUIDSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - Solved Examples
11 Videos
- NEWTON'S LAWS OF MOTION 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Integer type
1 Videos
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Integer
11 Videos
Similar Questions
Two uniform solid of masses m1 and m2 and radii r1 and r2 respectively, are connected at the ends of a uniform rod of length l and mass m. Find the moment of inertia of the system about an axis perpendicular to the rod and passing through a point at a distance of a from the centre of mass of the rod as shown in figure.

View SolutionA thin uniform rod AB of mass m and length L is placed on a smooth horizontal table. A constant horizontal force of magnitude F starts acting on the rod at one of the ends AB, Initially, the force is perpendicular to the length of the rod. Taking the moment at which force starts acting as t=0, find.
(a) Distance moved by centre of mass of the rod in time t0.
(b) Magnitude of initial acceleration of the end A of the rod.
View SolutionA uniform rod of length L pivoted at the bottom of a pond of depth L/2 stays in stable equilibrium as shown in the figure.

Find the force acting at the pivoted end of the rod in terms of mass m of the rod.
View SolutionA point negative charge -Q is placed at a distance r from a dipole with dipole moment P in the xy plane as shown in fig. The x-component of force acting on the charge-Q is
View SolutionA rod of length L and mass M is acted on by two unequal force F1andF2(<F1) as shown in the following figure.

The tension in the rod at a distance y from the end a is given by
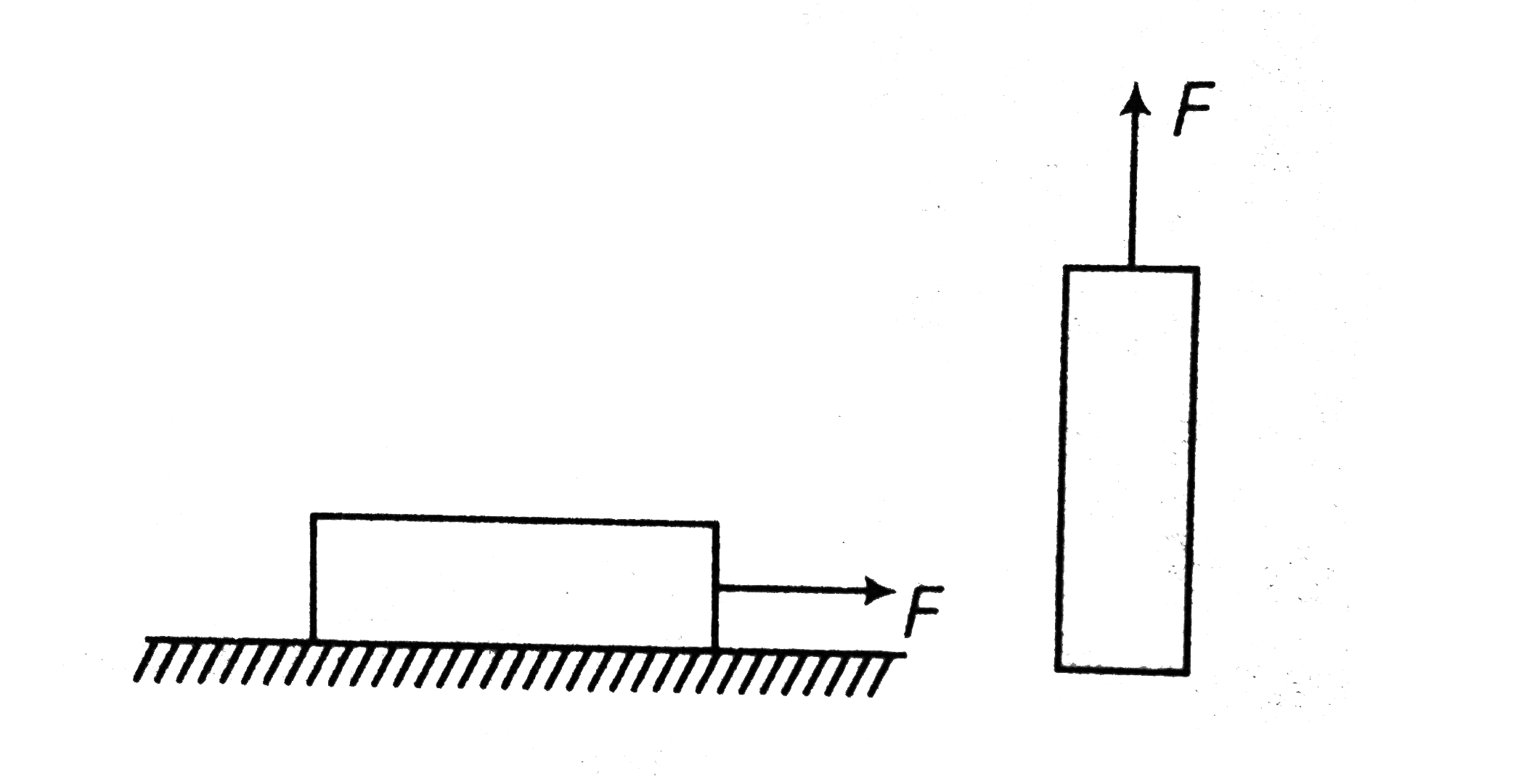
View SolutionAssertion: A uniform elastic rod lying on smooth horizontal surface is pulled by a constant horizontal force of magnitude F as shown in the figure. Another identical elastic rod is pulled vertically upwards by a constant vertical force of magnitude F as shown in the figure . the extensions in both the rods will be same.
Reason : In a uniform elastic rod, the extension depends only on forces acting at the ends of rods.
View SolutionA particle of mass m is situated at a distance d from one end of a rod of mass M and length L as shown in diagram. Find the magnitude of the gravitational force between them

View SolutionThe forces each of magnitude 10N act vertically upwards and downwards respectively at the two ends A and B of a uniform rod of length 4m which is pivoted at its mid point O as shown is fig. 1.30, Determine the magnitude of the resultant moment of forces about the pivot O.

View SolutionTwo forces each of magnitude 2N act vertically upwards and downwards respectively at the two ends of a uniform rod of length 1m which is pivoted at its centre. Draw a diagram of the arrangement and determine the resultant moment of forces about the mid point of the rod.
View SolutionA rod of length l, has a uniform positive charge per unit length and a total charge Q. calculate the electric field at a point P located along the long axis of the rod and at a distance a from one end

View Solution
