A space vehicle approaching a planet has a speed v when it is very far from the planet At that moment tangent of its trajectory would miss the centre of the planet by distance R if the planet has mass M and radius r what is the smallest value of R in order that the resulting orbit of the space vehicle will just miss the surface of the planet?
a) rv[v2+2GMr]12
b) vr[1+2GMr]
c) rv[v2+2GMr]
d) 2GMvr
The correct Answer is:A
To solve the problem, we need to determine the smallest value of R such that the space vehicle just misses the surface of the planet while approaching with speed v. We will use the principles of conservation of momentum and conservation of energy.
1. Understanding the Setup:
- Let the mass of the planet be M and its radius be r.
- The space vehicle has a speed v when it is very far from the planet.
- The trajectory of the vehicle will miss the center of the planet by a distance R.
2. Conservation of Momentum:
- At point A (far away from the planet), the momentum of the vehicle is mv.
- At point B (just missing the planet), the momentum is mv′, where v′ is the speed of the vehicle at that point.
- The perpendicular distance from the center of the planet to the trajectory is R.
- From conservation of momentum, we can write:
mv=mv′⋅Rr
- Rearranging gives:
v′=vRr
3. Conservation of Energy:
- At point A, the total energy is purely kinetic:
EA=12mv2
- At point B, the total energy includes both kinetic and potential energy:
EB=12mv′2−GMmR
- Setting EA=EB:
12mv2=12mv′2−GMmR
4. Substituting for v′:
- Substitute v′=vRr into the energy equation:
12mv2=12m(vRr)2−GMmR
- Simplifying gives:
12mv2=12mv2R2r2−GMmR
5. Eliminating m:
- Since m appears in every term, we can cancel it out:
12v2=12v2R2r2−GMR
6. Rearranging the Equation:
- Rearranging gives:
GMR=12v2R2r2−12v2
- Multiply through by 2R:
2GM=v2R3r2−v2R
- Rearranging leads to:
v2R3r2−v2R−2GM=0
7. Solving the Cubic Equation:
- This is a cubic equation in R. Using the cubic formula or numerical methods, we can find the smallest positive root.
8. Final Expression for R:
- The smallest value of R can be expressed as:
R=2GMv2(1+√1+4GMv2r2)
- Let the mass of the planet be M and its radius be r.
- The space vehicle has a speed v when it is very far from the planet.
- The trajectory of the vehicle will miss the center of the planet by a distance R.
- At point A (far away from the planet), the momentum of the vehicle is mv.
- At point B (just missing the planet), the momentum is mv′, where v′ is the speed of the vehicle at that point.
- The perpendicular distance from the center of the planet to the trajectory is R.
- From conservation of momentum, we can write:
mv=mv′⋅Rr
- Rearranging gives:
v′=vRr
- At point A, the total energy is purely kinetic:
EA=12mv2
- At point B, the total energy includes both kinetic and potential energy:
EB=12mv′2−GMmR
- Setting EA=EB:
12mv2=12mv′2−GMmR
- Substitute v′=vRr into the energy equation:
12mv2=12m(vRr)2−GMmR
- Simplifying gives:
12mv2=12mv2R2r2−GMmR
- Since m appears in every term, we can cancel it out:
12v2=12v2R2r2−GMR
- Rearranging gives:
GMR=12v2R2r2−12v2
- Multiply through by 2R:
2GM=v2R3r2−v2R
- Rearranging leads to:
v2R3r2−v2R−2GM=0
- This is a cubic equation in R. Using the cubic formula or numerical methods, we can find the smallest positive root.
- The smallest value of R can be expressed as:
R=2GMv2(1+√1+4GMv2r2)
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GRAVITATIONEXERCISE - Multiple Correct24videos
GRAVITATION
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GRAVITATIONEXERCISE - Assertion- Reasoning13videos
GRAVITATION
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GRAVITATIONEXERCISE - Subjective15videos
GRAVITATION
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - INTEGER_TYPE1videos
FLUID MECHANICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-1EXERCISE - Integer9videos
KINEMATICS-1
Similar Questions
A spaceship is sent to investigate a planet of mass M and radius R. While hanging motionless in space at a distance 5R from the centre of the planet, the spaceship fires an instrument package of mass m, which is much smaller than the mass of the spaceship. For what angle θ will the package just graze the surface of the planet?
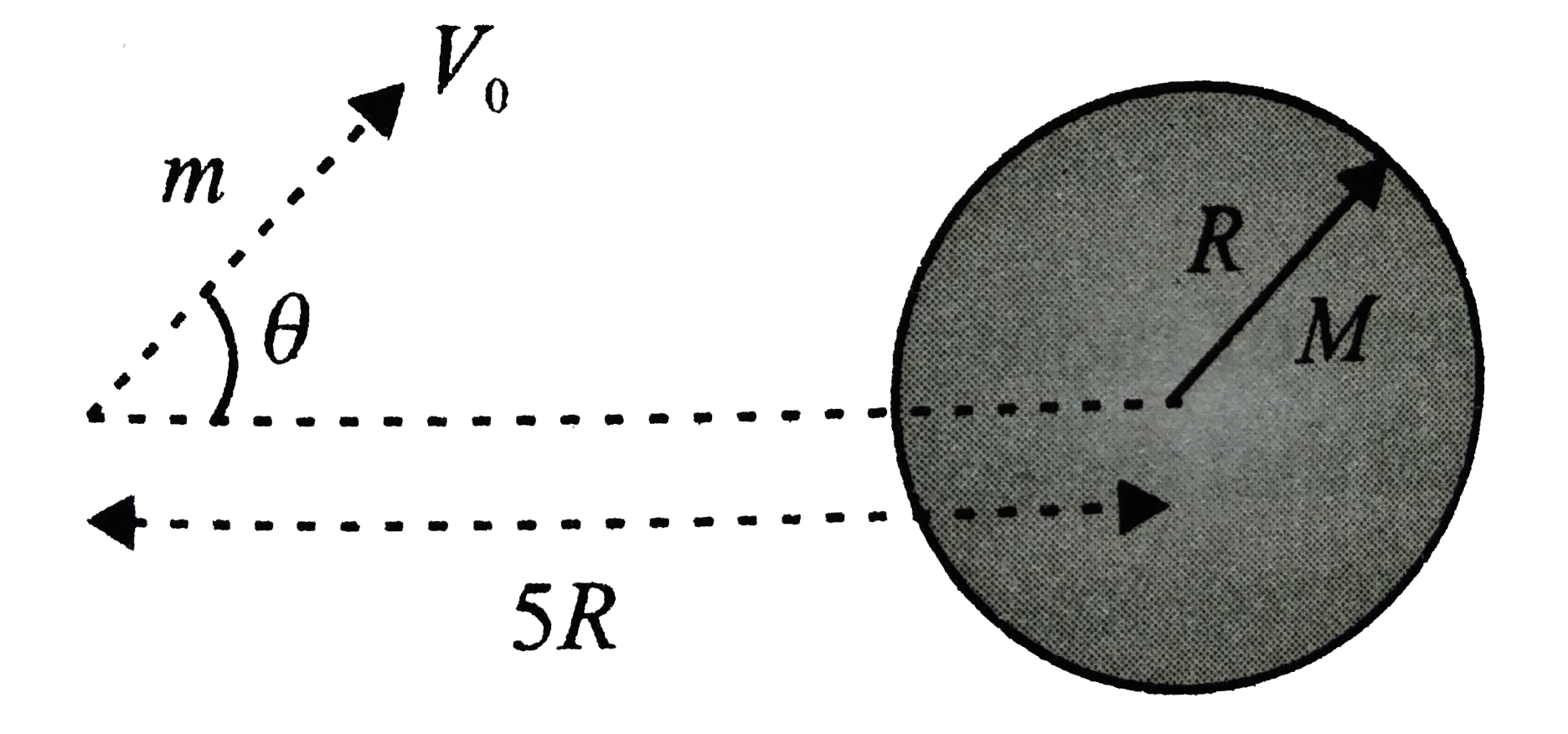 View Solution
View SolutionA spaceship is sent to investigate a planet of mass M and radius R. While hanging motionless in space at a distance 5R from the centre of the planet, the spaceship fires an instrument package of mass m, which is much smaller than the mass of the spaceship. For what angle θ will the package just graze the surface of the planet?
 View Solution
View SolutionWhat is the mass of the planet that has a satellite whose time period is T and orbital radius is r?
View SolutionA body is moving in a low circular orbit about a planet of mass M and radius R. The radius of the orbit can be taken to be R itself. Then the ratio of the speed of this body in the orbit to the escape velocity from the planet is :
View SolutionA spherical planet far out in space has mass 2M and radius a. A particle of mass m is falling freely near its surface. What will be the acceleration of that particle ?
View SolutionA body of mass m at inifnity is approaching the centre of a hypothetical hollow planet of mass M and radius R. The speed of the body when it passes the centre of the planet through a diametrical tunnel is
View SolutionWhat is the minimum energy required to launch a satellite of mass m from the surface of a planet of mass M and radius R in a circular orbit at an altitude of 2R?
View SolutionA planet is revolving round the sun in an elliptical orbit, If v is the velocity of the planet when its position vector from the sun is r, then areal velocity of the planet is
View SolutionA hypothetical planet in the shape of a sphere is completely made of an incompressible fluid and has a mass M and radius R. If the pressure at the surface of the planet is zero, then the pressure at the centre of the planet is [G = universal constant of gravitation]
View SolutionThe work done by gravitational force on a point mass m0in moving from the surface of a planet off mass M and radius R to a height R2 is
View Solution

