A double star consists of two stars having masses M and 2M. The distance between their centres is equal to r. They revolve under their mutual gravitational interaction. Then, which of the following statements are not correct?
r32
r
m12
m−12
The correct Answer is:A, D
r2=2mrm+2m=2r3
T22=4π2r22GM⇒T22=32π2r327Gm
T2∝r22 and T2∝m12 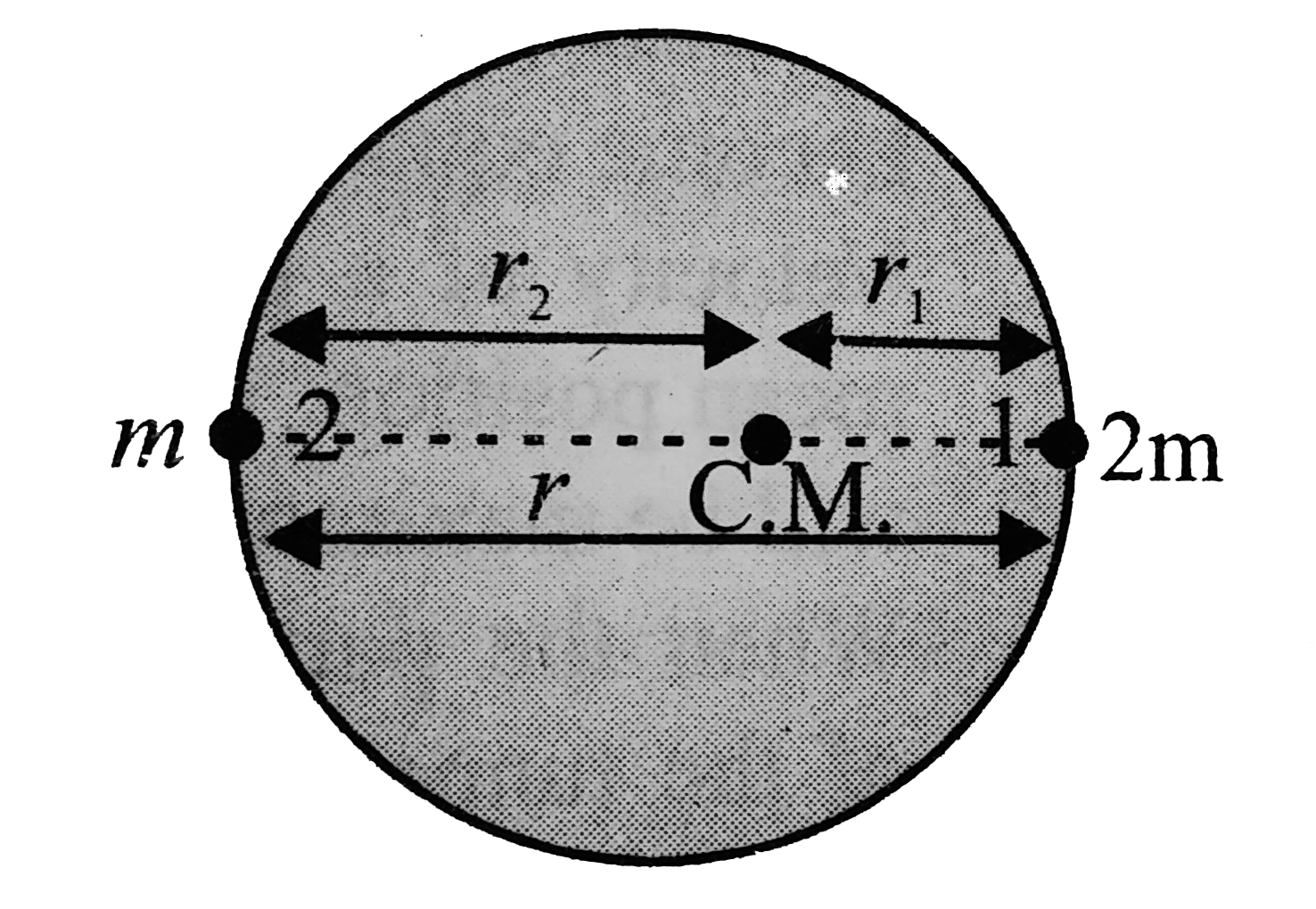
Topper's Solved these Questions
- GRAVITATIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GRAVITATIONEXERCISE - Multiple Correct
24 Videos
- GRAVITATIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GRAVITATIONEXERCISE - Assertion- Reasoning
13 Videos
- GRAVITATIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GRAVITATIONEXERCISE - Subjective
15 Videos
- FLUID MECHANICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - INTEGER_TYPE
1 Video
- KINEMATICS-1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-1EXERCISE - Integer
9 Videos
Similar Questions
A double star is a system of two stars of masses m and 2m, rotating about their centre of mass only under their mutual gravitational attraction. If r is the separation between these two stars then their time period of rotation about their centre of mass will be proportional to
View Solution_E01_055_Q01.png)
For the double star system, the two stars having masses m1 and m2are separated b a distance r. They are revolving about their common centre of mass in radii r1 and r2 respectively. Which of the following is/are incorrect.?
View Solution
Knowledge Check
Two stars of masses m1 and m2 distance r apart, revolve about their centre of mass. The period of revolution is :
A2π√r32G(m1+m2)B2π√r3(m1+m2)2G(m1m2)C2π√2r3G(m1+m2)D2π√r3G(m1+m2)Two particles of equal mass go around a circle of radius R under the action of their mutual gravitational attraction. The speed v of each particle is
A12R√(1Gm)B√(Gm2R)C12√(GmR)D√(4GmR)
If the masses of two bodies are quadrupled and the distance between their centres is doubled, then how many times the force of gravitation between them will be changed ?
View SolutionTwo stars of masses m1 and m2 distance r apart, revolve about their centre of mass. The period of revolution is :
View SolutionTwo bodies of different masses 2kg and 4kg are moving with velocities 2m/s and 10m/s towards each other due to mutual gravitational attraction. Then the velocity of the centre of mass is
View SolutionThree particles of equal mass M each are moving on a circular path with radius r under their mutual gravitational attraction. The speed of each particle is
View SolutionTwo objects of masses m and 4m are at rest at an infinite separation. They move towards each other under mutual gravitational attraction. If G is the universal gravitaitonal constant, then at separation r
View SolutionTwo particles of equal mass go round a circle of radius R under the action of their mutual gravitational attraction. Find the speed of each particle.
View Solution