A flat square sheet of charge (side 50 cm) carries a uniform surface charge density. An electrons0.5 cm form a point near the center of the sheet experiences a force of 1.8×10−12N directed away from the sheet. Determine the total charge on the sheet.
The correct Answer is:−50μC
To determine the total charge on the square sheet, we will follow these steps:
Step 1: Understand the relationship between electric field (E), surface charge density (σ), and total charge (Q).
The electric field (E) due to an infinite sheet of charge is given by the formula:
E=σ2ϵ0
where:
- σ is the surface charge density,
- ϵ0 is the permittivity of free space, approximately 8.854×10−12C2/N m2.
Step 2: Relate surface charge density to total charge.
The surface charge density (σ) can also be expressed in terms of total charge (Q) and area (A):
σ=QA
where A is the area of the sheet.
Step 3: Calculate the area of the square sheet.
Given that the side of the square sheet is 50 cm, we convert this to meters:
Side=0.5m
Thus, the area A is:
A=Side2=(0.5m)2=0.25m2
Step 4: Substitute the expression for σ into the electric field formula.
Substituting σ into the electric field formula gives:
E=Q2ϵ0A
Step 5: Relate the force experienced by the electron to the electric field.
The force F experienced by a charge e (the charge of the electron) in an electric field E is given by:
F=eE
where e=1.6×10−19C.
Step 6: Substitute the expression for E into the force equation.
We can substitute the expression for E into the force equation:
F=e(Q2ϵ0A)
Step 7: Rearrange the equation to solve for total charge Q.
Rearranging the equation for Q gives:
Q=2ϵ0AFe
Step 8: Substitute the known values into the equation.
Now we can substitute the known values:
- ϵ0=8.854×10−12C2/N m2
- A=0.25m2
- F=1.8×10−12N
- e=1.6×10−19C
Substituting these values:
Q=2×(8.854×10−12)×(0.25)×(1.8×10−12)1.6×10−19
Step 9: Calculate the total charge Q.
Calculating this gives:
Q≈2×8.854×10−12×0.25×1.8×10−121.6×10−19
Q≈−5.0×10−5C
or
Q≈−50μC
Final Answer:
The total charge on the sheet is approximately −50μC.
---
The electric field (E) due to an infinite sheet of charge is given by the formula:
E=σ2ϵ0
where:
- σ is the surface charge density,
- ϵ0 is the permittivity of free space, approximately 8.854×10−12C2/N m2.
The surface charge density (σ) can also be expressed in terms of total charge (Q) and area (A):
σ=QA
where A is the area of the sheet.
Given that the side of the square sheet is 50 cm, we convert this to meters:
Side=0.5m
Thus, the area A is:
A=Side2=(0.5m)2=0.25m2
Substituting σ into the electric field formula gives:
E=Q2ϵ0A
The force F experienced by a charge e (the charge of the electron) in an electric field E is given by:
F=eE
where e=1.6×10−19C.
We can substitute the expression for E into the force equation:
F=e(Q2ϵ0A)
Rearranging the equation for Q gives:
Q=2ϵ0AFe
Now we can substitute the known values:
- ϵ0=8.854×10−12C2/N m2
- A=0.25m2
- F=1.8×10−12N
- e=1.6×10−19C
Q=2×(8.854×10−12)×(0.25)×(1.8×10−12)1.6×10−19
Calculating this gives:
Q≈2×8.854×10−12×0.25×1.8×10−121.6×10−19
Q≈−5.0×10−5C
or
Q≈−50μC
The total charge on the sheet is approximately −50μC.
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - COULOMB LAW AND ELECTRIC FIELDEXERCISE - Single Correct47videos
COULOMB LAW AND ELECTRIC FIELD
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - COULOMB LAW AND ELECTRIC FIELDEXERCISE - Multiple Correct8videos
COULOMB LAW AND ELECTRIC FIELD
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - COULOMB LAW AND ELECTRIC FIELDEXERCISE - Subjective Type15videos
COULOMB LAW AND ELECTRIC FIELD
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENGAGE PHYSICS DPPEXERCISE - subjective type51videos
CENGAGE PHYSICS DPP
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC CURRENT & CIRCUITSEXERCISE - Kirchhoff s law and simple circuits15videos
ELECTRIC CURRENT & CIRCUITS
Similar Questions
A long thin flat sheet has a uniform surface charge density σ. The magnitude of the electric field at a distance .r. from it is given by
View SolutionA conducting sphere fo radius 10 cm has an unknown charge. If the electric field 20 cm from the center of the sphere is 1.5×103N/C and points radially inwards, what is the net charge on the sphere ?
View SolutionA uniformly charged square plate having side L carries a uniform surface charge density σ. The plate lies in the y−z plane with its centre at the origin. A point charge q lies on the x-axis. The flux of the electric field of q through the plate is ϕ0, while the foce on the point charge q due to the plate is F0, along the x-axis. Then,
View SolutionTwo infinite, non-conducting sheets of charge are parallel to each other, as shown in figure. The sheet on the left has a uniform surface charge density σ, and the one on the right has a uniform charge density −σ. Calculate the electric field at points (a) to the left of, (b) in between, and (c) to the right of the two sheets.
 View Solution
View SolutionAn infinite thin plane sheet of charge density 7.08×10−11(C/m2) is held in air. Find the electric field at a point very close to the sheet.
View SolutionWhat is the net charge on a conducting sphere of radius 10 cm ? Given that the electric field 15 cm from the center of the sphere is equal to 3×103 N/C and is directed inward
View SolutionIn the figure shown there is a large sheet of charge of uniform surface charge density'σ'.A charge particle of charge '−q' and mass 'm' is projected from a point A on the sheet with a speed 'u' with the angle of projection such that it lands at maximum distance from A on the sheet. Neglecting gravity, find the time flight
 View Solution
View SolutionA large insulating thick sheet of thickness 2d is charged with a uniform volume charge density p. A particle of mass m, carrying a charge q having a sign opposite to that of the sheet, is released from the surface of the sheet. The sheet does not offer any mechanical resistance to the motion of the particle. Find the oscillation frequency v of the particle inside the sheet
View SolutionA large sheet carries uniform surface charge density σ . A rod of length 2l has a linear charge density λ on one half and −λ on the second half. The rod is hinged at the midpoint O and makes an angle θ with the normal to the sheet. The torque experience by the rod is
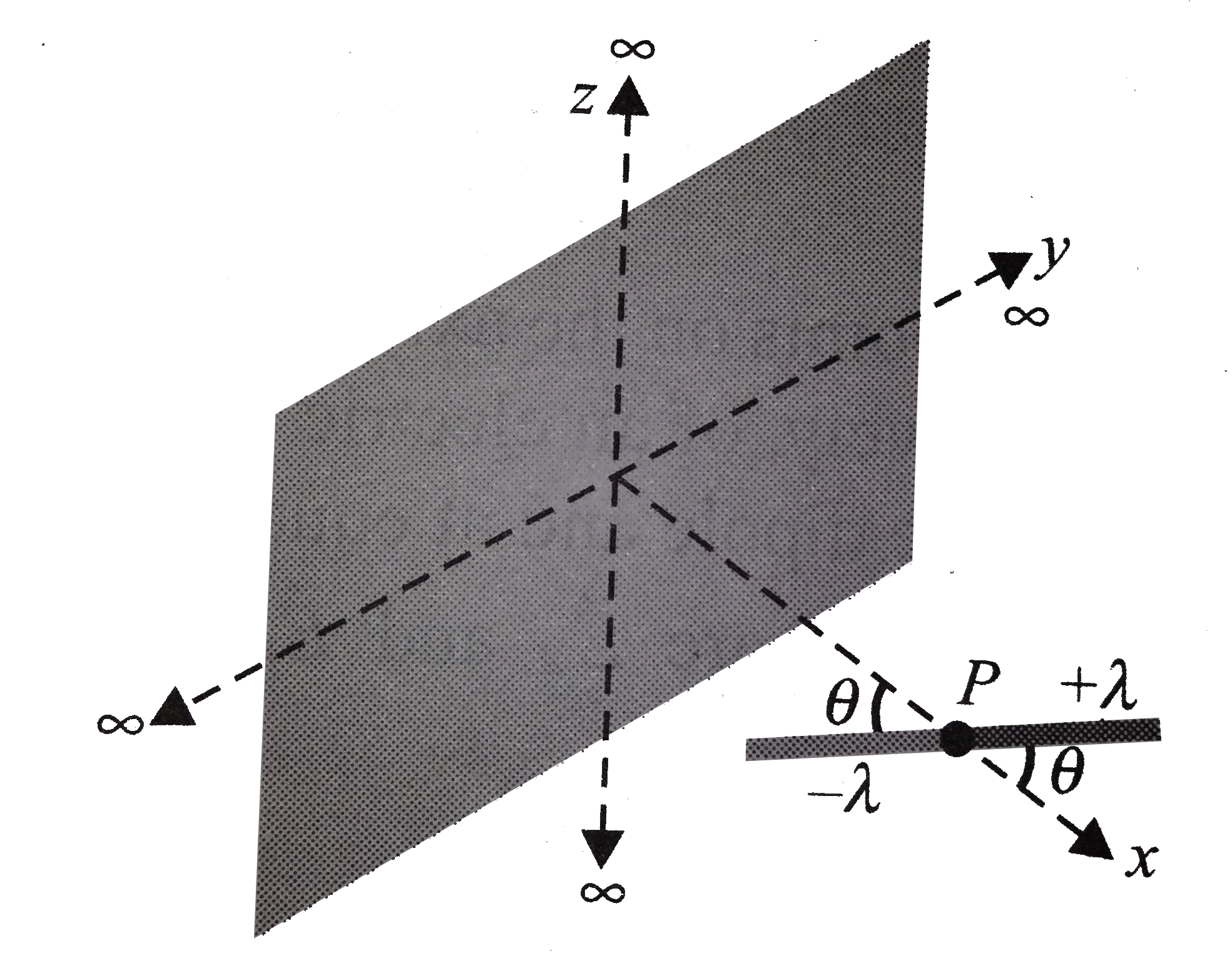 View Solution
View SolutionAn infinite sheet of charge has a surfaces charge density of 10−7Cm2. The separation between two equipotential surfce whose potentials differ by 5V is
View Solution

