A positively charged ball hangs from a long silk thread. Electric filed at a certain point (at the same horizontal level of ball) due to this charge is E. Let us put a positive test charge q0 at this point and measure F/q0 on this charges. then E
>F/q0
<F/q0
=F/q0
none of these
The correct Answer is:A
To solve the problem, we need to analyze the situation of a positively charged ball hanging from a silk thread and the effect of placing a positive test charge q0 at a certain point in the electric field created by the charged ball.
1. Understanding the Setup:
- We have a positively charged ball with charge Q hanging from a silk thread.
- The electric field E at a certain horizontal point P (at the same level as the ball) due to this charge is given by the formula:
E=kQr2
where k is Coulomb's constant and r is the distance from the charge to point P.
Hint: Remember that the electric field due to a point charge is directed away from the charge if it is positive.
2. Placing the Test Charge:
- We place a positive test charge q0 at point P.
- The force F experienced by the test charge due to the electric field E is given by:
F=q0E
Hint: The force on a charge in an electric field is the product of the charge and the electric field strength.
3. Calculating the Electric Field with the Test Charge:
- When we place the test charge q0, it will experience a repulsive force due to the charged ball. This will cause the silk thread to move, changing the distance between the ball and the point P to a new distance r′.
- The new electric field E′ at point P (after placing q0) can be expressed as:
E′=Fq0=kQr′2
Hint: The electric field is still defined as the force per unit charge, but now the distance has changed.
4. Comparing Distances:
- Since the test charge q0 is repelled by the positively charged ball, the new distance r′ will be greater than the original distance r (i.e., r′>r).
- Therefore, we can conclude that:
E′=kQr′2<kQr2=E
Hint: The electric field decreases with increasing distance from the charge.
5. Final Conclusion:
- Since E′<E, we can state that:
E>Fq0
- Thus, the electric field E at point P is greater than the force per unit charge Fq0.
Hint: This relationship shows how the presence of the test charge affects the electric field and the forces involved.
Final Answer:
E>Fq0
- We have a positively charged ball with charge Q hanging from a silk thread.
- The electric field E at a certain horizontal point P (at the same level as the ball) due to this charge is given by the formula:
E=kQr2
where k is Coulomb's constant and r is the distance from the charge to point P.
- We place a positive test charge q0 at point P.
- The force F experienced by the test charge due to the electric field E is given by:
F=q0E
- When we place the test charge q0, it will experience a repulsive force due to the charged ball. This will cause the silk thread to move, changing the distance between the ball and the point P to a new distance r′.
- The new electric field E′ at point P (after placing q0) can be expressed as:
E′=Fq0=kQr′2
- Since the test charge q0 is repelled by the positively charged ball, the new distance r′ will be greater than the original distance r (i.e., r′>r).
- Therefore, we can conclude that:
E′=kQr′2<kQr2=E
- Since E′<E, we can state that:
E>Fq0
- Thus, the electric field E at point P is greater than the force per unit charge Fq0.
E>Fq0
Topper's Solved these Questions
- COULOMB LAW AND ELECTRIC FIELDBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - COULOMB LAW AND ELECTRIC FIELDEXERCISE - Multiple Correct
8 Videos
- COULOMB LAW AND ELECTRIC FIELDBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - COULOMB LAW AND ELECTRIC FIELDEXERCISE - Comprehension
25 Videos
- COULOMB LAW AND ELECTRIC FIELDBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - COULOMB LAW AND ELECTRIC FIELDEXERCISE - Subjective
32 Videos
- CENGAGE PHYSICS DPPBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENGAGE PHYSICS DPPEXERCISE - subjective type
51 Videos
- ELECTRIC CURRENT & CIRCUITSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC CURRENT & CIRCUITSEXERCISE - Kirchhoff s law and simple circuits
15 Videos
Similar Questions
A positive point charge Q is bruought mear an isolated metal cube.
View SolutionA positive point charge q is brought near a neutral metal sphere.
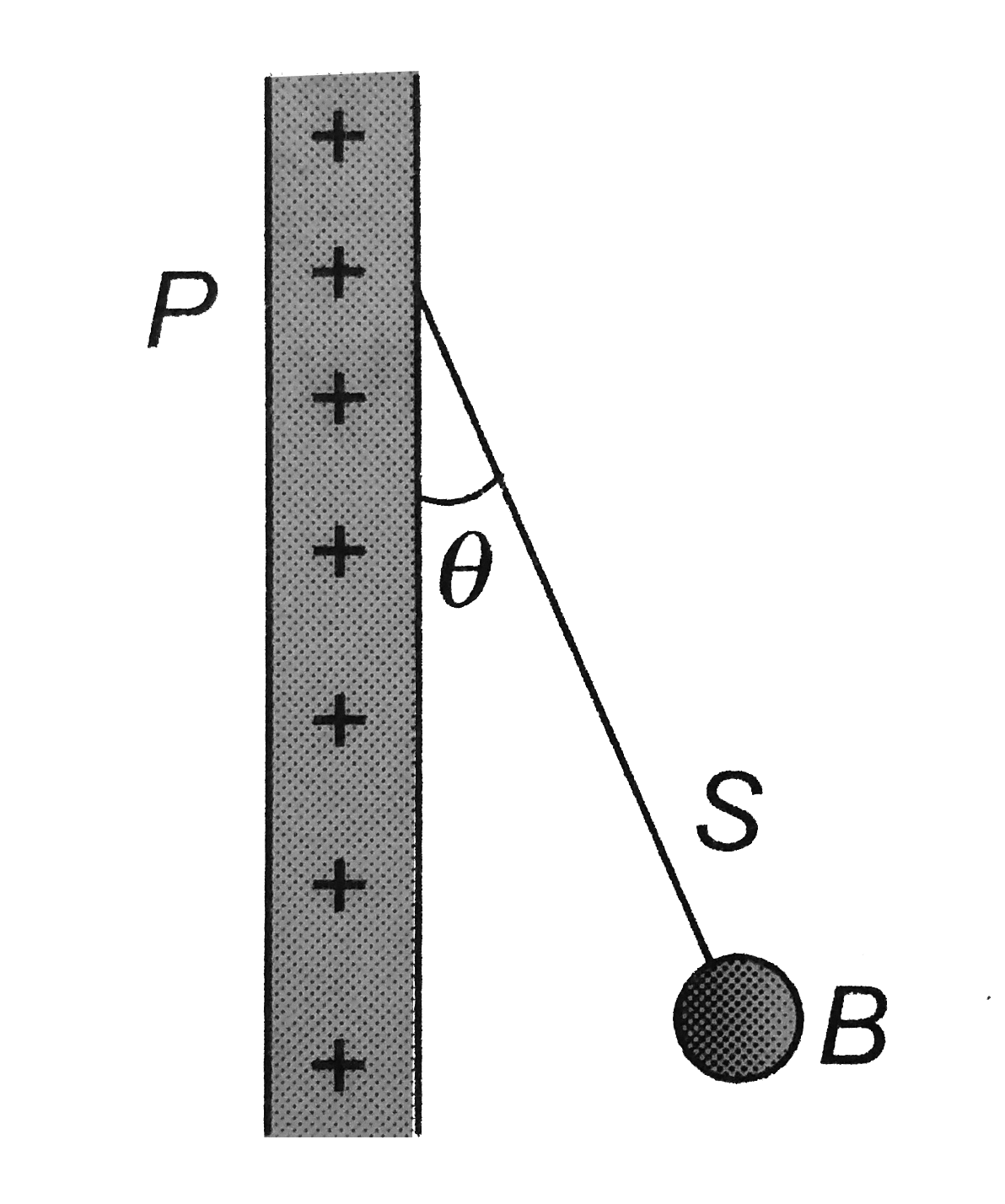
View SolutionA charged ball B hangs from a silk thread S, which makes an angle θ with a large charged conducting sheet P, as shown in the figure. The surface charge density σ of the sheet is proportional to
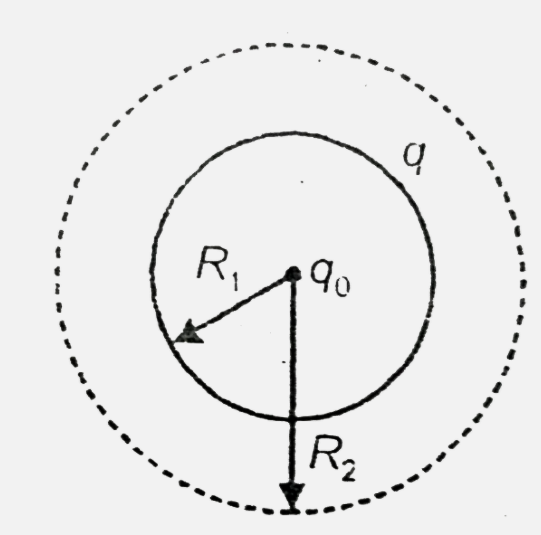
View SolutionA sperical shell is uniformly charged by a charge q. A point charge q0 is at its centre , then
View SolutionA positive point charge Q is brought near an isolated metal cube then what will happen to the charge of cube?
View SolutionA positively charged ring is in y - z plane with its centre at origin . A positive test charge qe , held at origin is released along x axis, then its speed
View SolutionA positive point charge q is placed at a distance 2 R from the surface of a metallic shell of radius R. the electric field at centre of shell due to indouced charge has magnitude
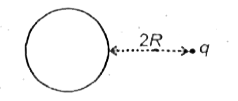
View SolutionA positive point charge q1 is placed at (a,0) and another positive point charge q2 is placed at (0,a) . Find the force acting on q1.
View SolutionTwo point charges +Q and -Q are separated by a certain distance. The resultant electric field is parallel to the line joining the charges at the points
View SolutionA point charge q is placed at the origin . How does the electric field due to the charge very with distance r from the origin ?
View Solution
