Threee charges +Q1,+Q2 and q are placed on a straight line such that q is somewhere in between +Q1and Q2. If this system of charges is in equlibirium what should be the magnitude and sign of charge q?
Q1Q2(√Q1+√Q2)2, positive
Q1+Q22, positive
Q1Q2(√Q1+√Q2)2, Negative
Q1+Q22,Negative
The correct Answer is:C
To solve the problem of finding the magnitude and sign of charge q placed between two positive charges +Q1 and +Q2 such that the system is in equilibrium, we can follow these steps:
Step 1: Understand the Forces Acting on Charge q
Since +Q1 and +Q2 are both positive charges, they will repel each other. The charge q must be negative for it to be attracted to both +Q1 and +Q2 to maintain equilibrium. Therefore, we conclude that:
- Charge q must be negative.
Step 2: Set Up the Equilibrium Condition
For the charge q to be in equilibrium, the net force acting on it must be zero. The forces acting on q due to +Q1 and +Q2 can be expressed as:
- The force exerted by +Q1 on q (attractive force) is given by:
F1=kQ1|q|x2
- The force exerted by +Q2 on q (also attractive) is given by:
F2=kQ2|q|(L−x)2
Where:
- k is Coulomb's constant,
- x is the distance from +Q1 to q,
- L is the total distance between +Q1 and +Q2.
Step 3: Equate the Forces
For equilibrium, we set the magnitudes of these forces equal to each other:
F1=F2
This gives us:
kQ1|q|x2=kQ2|q|(L−x)2
We can cancel k and |q| (since q is negative, we consider the magnitude):
Q1x2=Q2(L−x)2
Step 4: Cross-Multiply and Rearrange
Cross-multiplying gives:
Q1(L−x)2=Q2x2
Expanding this leads to:
Q1(L2−2Lx+x2)=Q2x2
Rearranging gives:
Q1L2−2Q1Lx+(Q1−Q2)x2=0
Step 5: Solve the Quadratic Equation
This is a quadratic equation in x:
(Q1−Q2)x2−2Q1Lx+Q1L2=0
Using the quadratic formula x=−b±√b2−4ac2a, where:
- a=Q1−Q2,
- b=−2Q1L,
- c=Q1L2.
Step 6: Find the Magnitude of Charge q
From the equilibrium condition, we can express the magnitude of charge q:
|q|=Q1Q2(Q1Q2⋅(L−x)2)
Substituting x from the previous step will give us the magnitude of q.
Final Result
Thus, the magnitude and sign of charge q is:
q=−Q1Q2(√Q1+√Q2)2
Since +Q1 and +Q2 are both positive charges, they will repel each other. The charge q must be negative for it to be attracted to both +Q1 and +Q2 to maintain equilibrium. Therefore, we conclude that:
- Charge q must be negative.
For the charge q to be in equilibrium, the net force acting on it must be zero. The forces acting on q due to +Q1 and +Q2 can be expressed as:
- The force exerted by +Q1 on q (attractive force) is given by:
F1=kQ1|q|x2
- The force exerted by +Q2 on q (also attractive) is given by:
F2=kQ2|q|(L−x)2
- k is Coulomb's constant,
- x is the distance from +Q1 to q,
- L is the total distance between +Q1 and +Q2.
For equilibrium, we set the magnitudes of these forces equal to each other:
F1=F2
This gives us:
kQ1|q|x2=kQ2|q|(L−x)2
We can cancel k and |q| (since q is negative, we consider the magnitude):
Q1x2=Q2(L−x)2
Cross-multiplying gives:
Q1(L−x)2=Q2x2
Expanding this leads to:
Q1(L2−2Lx+x2)=Q2x2
Rearranging gives:
Q1L2−2Q1Lx+(Q1−Q2)x2=0
This is a quadratic equation in x:
(Q1−Q2)x2−2Q1Lx+Q1L2=0
Using the quadratic formula x=−b±√b2−4ac2a, where:
- a=Q1−Q2,
- b=−2Q1L,
- c=Q1L2.
From the equilibrium condition, we can express the magnitude of charge q:
|q|=Q1Q2(Q1Q2⋅(L−x)2)
Substituting x from the previous step will give us the magnitude of q.
Thus, the magnitude and sign of charge q is:
q=−Q1Q2(√Q1+√Q2)2
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - COULOMB LAW AND ELECTRIC FIELDEXERCISE - Multiple Correct8videos
COULOMB LAW AND ELECTRIC FIELD
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - COULOMB LAW AND ELECTRIC FIELDEXERCISE - Comprehension25videos
COULOMB LAW AND ELECTRIC FIELD
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - COULOMB LAW AND ELECTRIC FIELDEXERCISE - Subjective32videos
COULOMB LAW AND ELECTRIC FIELD
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENGAGE PHYSICS DPPEXERCISE - subjective type51videos
CENGAGE PHYSICS DPP
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC CURRENT & CIRCUITSEXERCISE - Kirchhoff s law and simple circuits15videos
ELECTRIC CURRENT & CIRCUITS
Similar Questions
Three charges −q,+Q and −q are placed in a straight line as shown

If the total potential energy of the system is zero, then the ratio qQ isView SolutionThree charges −q1,+q2 and −q3 are placed as shown in the figure. The x-component of the force on −q1 is proportional to
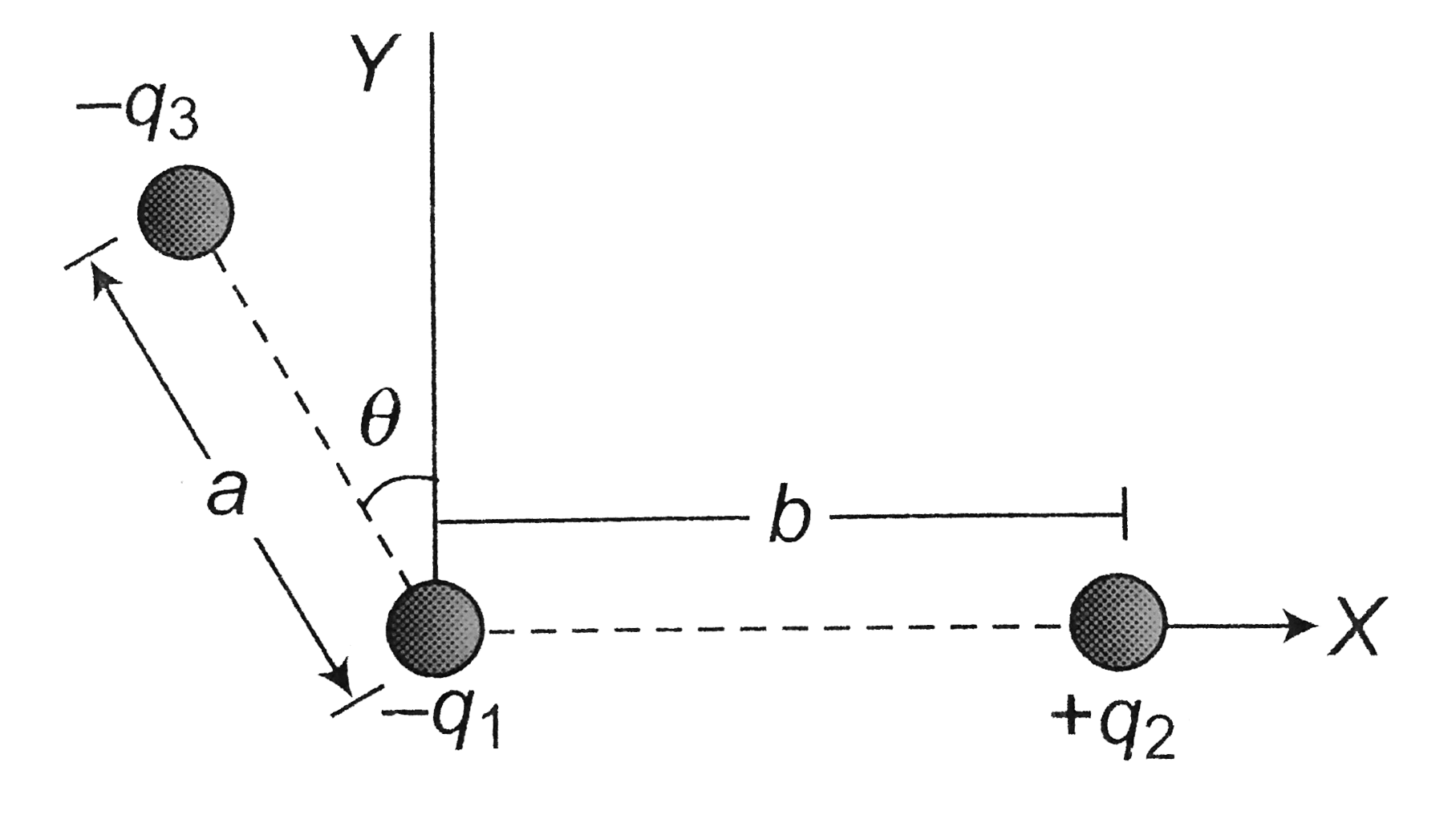 View Solution
View SolutionThree point charge Q,4Q and 16Q are placed on a straight line 9cm long.Charges are placed in such a way that the system has minimum potential energy .Then
View SolutionA charge q is placed at the centre of the line joining two equal charges Q. The system of the three charges will be in equilibrium if q is equal to:
View SolutionA charge q is placed at the centre of the line joining two equal charges Q. The system of the three charges will be in equilibrium if q is equal to:
View SolutionA charge q is placed at the centre of the line joining two equal charges Q. The system of the three charges will be in equilibrium if q is equal to:
View SolutionCharges−q,Q,and−q are placed at an equal distance on a straight liner. If the total potential energy of the system of three charges is zero, then find the ratio Q/q.
 .View Solution
.View SolutionThree point charges -Q, Q and Q are placed on a straight line with distance d between charges as shown. Find the magnitude of the electric field at the point P in the configuration shown which is at a distance a from middle charge Q in the system provided that a>>d. Take 2Qd=p.
 View Solution
View SolutionThe figure shown is a plot of electric field lines due to two charges Q1 and Q2 . The sign of charges is
 View Solution
View SolutionTwo point charges +q and +4q are a distance l apart. A third charge q1 is so placed that the entire system is in equilibrium. Find the location, magnitude and sign of the third charge.
View Solution

