A cube of side a is placed such that the nearest face , which is parallel to the yz plane , is at a distance a from the origin . The electric field components are
Ex=αx1/2,Ey=Ez=0.
The charge within the cube is

√2αε0a5/2
αε0a5/2
(√2−1)αε0a5/2
zero
The correct Answer is:C
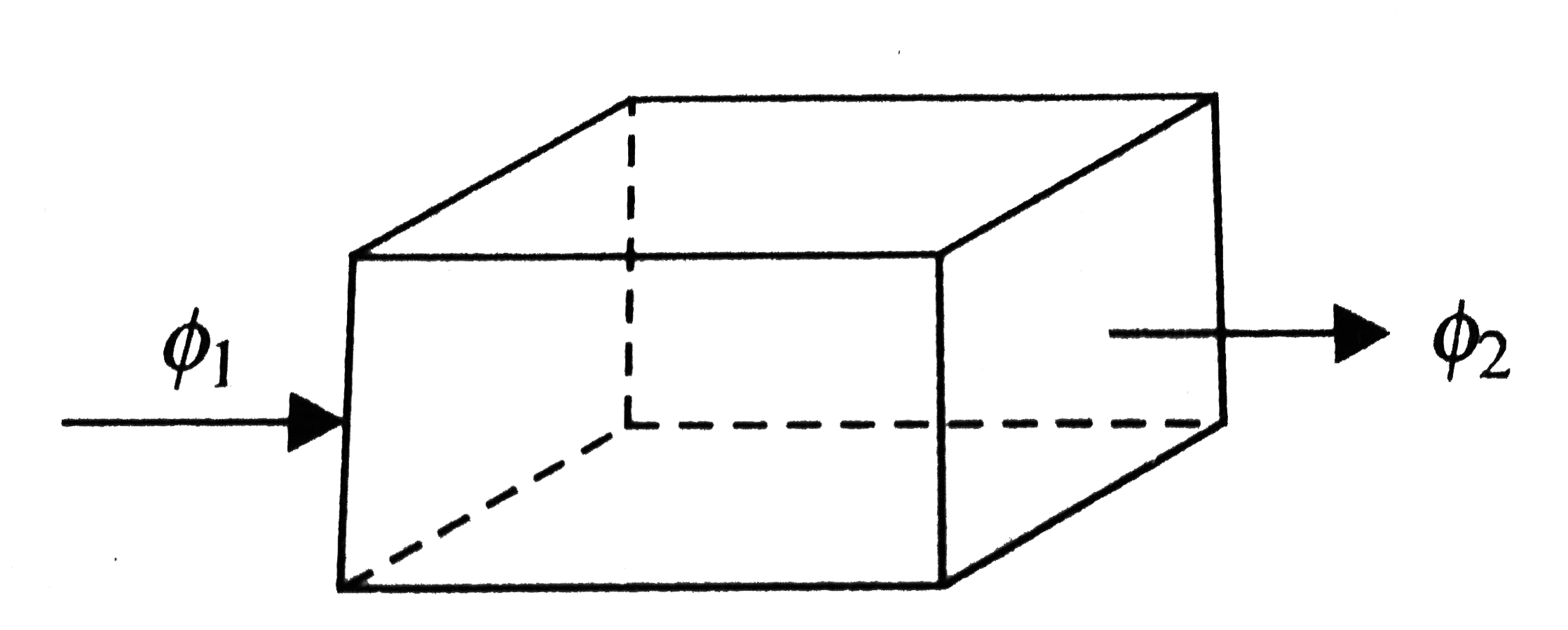
ϕ1=E1a2=−αa1/2a2=−αa5/2
and ϕ2=E2a2=α(2a)1/2a2=√2αa5/2
ϕnet=(√2−1)αa5/2
Using the Gauss theorem , we get
ϕ=q∈ε0
or q∈=ϕε0=(√2−1)ε0αa5/2
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC FLUX AND GAUSS LAWEXERCISE - Subjective type7videos
ELECTRIC FLUX AND GAUSS LAW
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC FLUX AND GAUSS LAWEXERCISE - MCQ s38videos
ELECTRIC FLUX AND GAUSS LAW
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC FLUX AND GAUSS LAWEXERCISE - Multiple Correct8videos
ELECTRIC FLUX AND GAUSS LAW
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC CURRENT AND CIRCUITEXERCISE - Interger8videos
ELECTRIC CURRENT AND CIRCUIT
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC POTENTIALEXERCISE - DPP 3.515videos
ELECTRIC POTENTIAL
Similar Questions
A cube of side a is placed such that the nearest face , which is parallel to the yz plane , is at a distance a from the origin . The electric field components are
Ex=αx1/2,Ey=Ez=0.
The flux ϕE through the cube is
 View Solution
View SolutionDue to a charge inside a cube the electric field is Ex=600x1/2,Ey=0,Ez=0. The charge inside the cube is (approximately):
 View Solution
View SolutionAn equation of a plane parallel to the plane x−2y+2z−5=0 and at a unit distance from the origin is
View SolutionFind the equations of the planes parallel to the plane x−2y+2z−3=0 which is at a unit distance from the point (1,2,3).
View SolutionThe electric components in the figure are Ex=αx1/2,Ey=0,Ez=0 where α=800N/m2 if a=0.1m is the side of cube then the charge with in the cube is
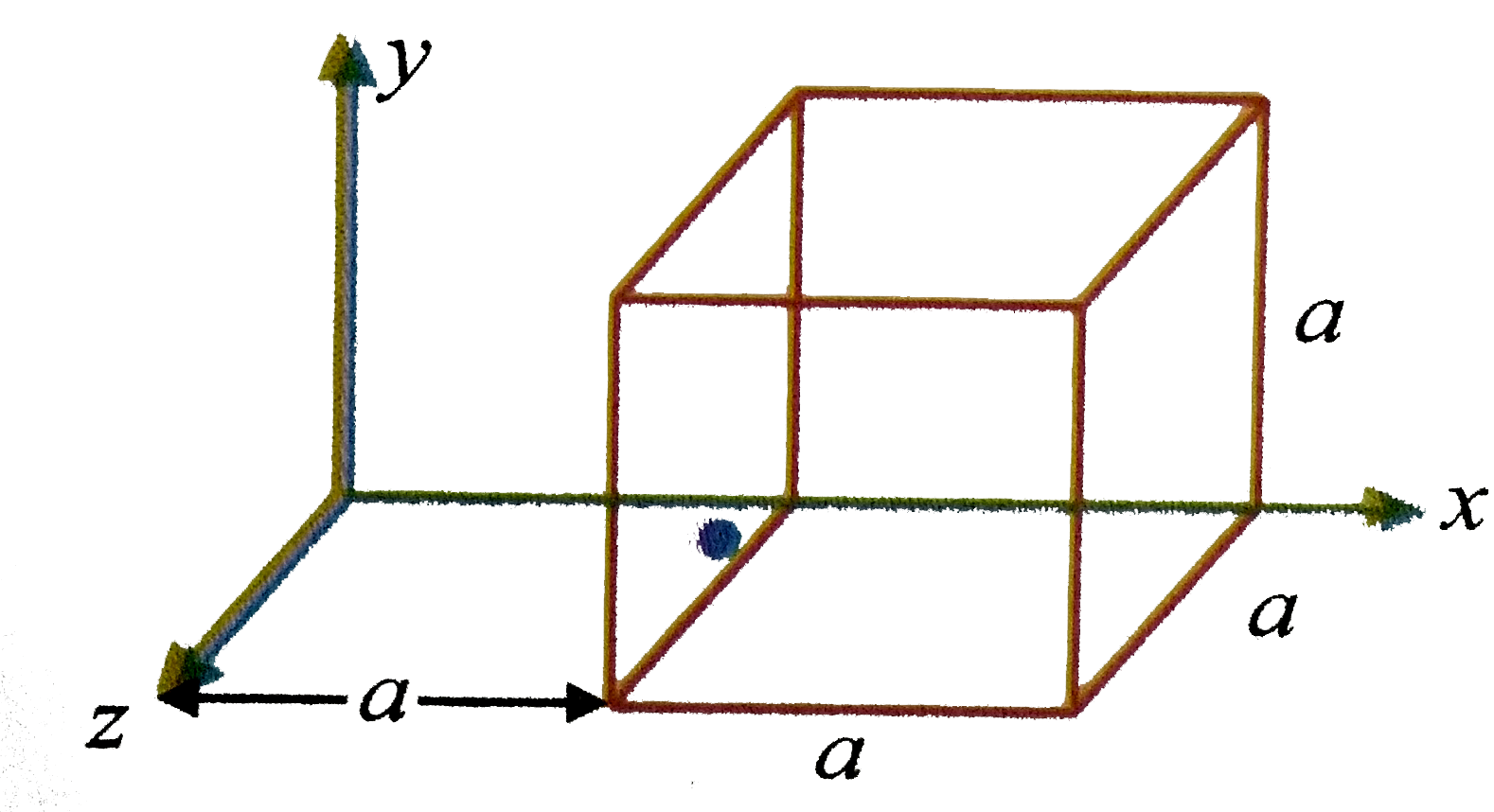 View Solution
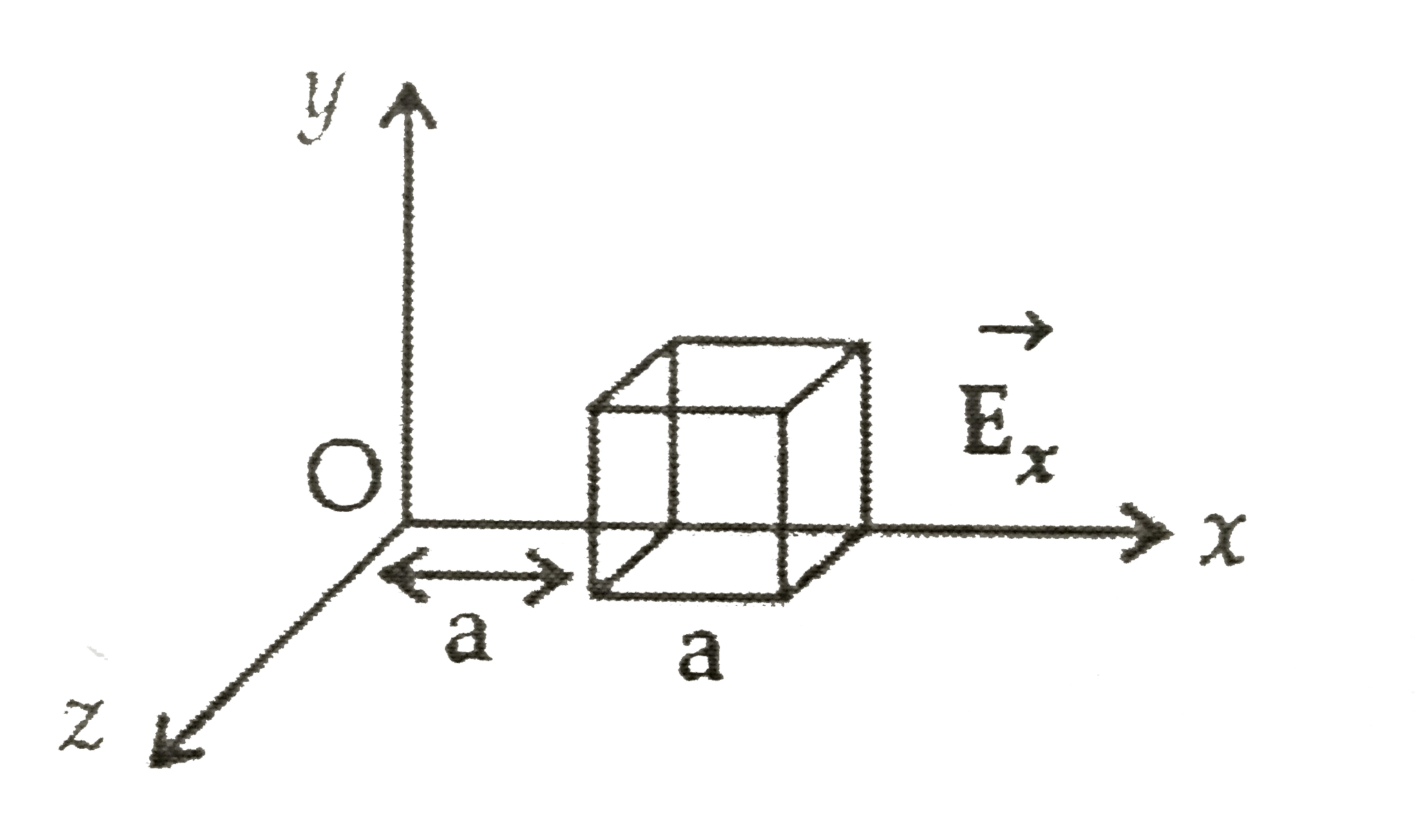
View SolutionDefine electric flux and write its SI unit . The electric field components in the figure shown are : Ex=αx,Ey=0,Ez=0 where α=100NCm.
Calculate the charge within the cube , assuming a = 0.1 m .
 View Solution
View SolutionFind the equations of the plane parallel to the plane x−2y+2z−3=0 and which are at a unit distance from the point (1, 1, 1).
View SolutionTwo charges e and 3e are placed at a distance r. The distance of the point where the electric field intensity will be zero is
View SolutionAn electromagnetic wave is propagating in vacuum along z-axis, the electric field component is given by Ex=E0sin(kz−ωt). Then magnetic components is
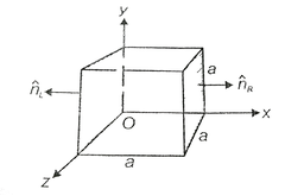
View SolutionThe electric field components in the figure below are Ex=800x2N/C,Ey=Ez=0.
Calculate
(1) The flux throught he cube and
(2) The charge withing the cube
Assume that a =0.1 m
 View Solution
View Solution

