Two small particles A and B having masses m=0.5kg each and charges q1=(−155/18μC) and q2=(+100μC), respectively, are connected at the ends of a nonconducting, flexible, and inextensible string of length r=0.5m.
Particle A is fixed and B is whirled along a vertical circle with center at A. if a vertically upward electric field of Strength E=1.1×105NC−1 exists in the space, calculate the minimum velocity of particle B required at the highest point so that it may just complete the circle (g=10ms−2).
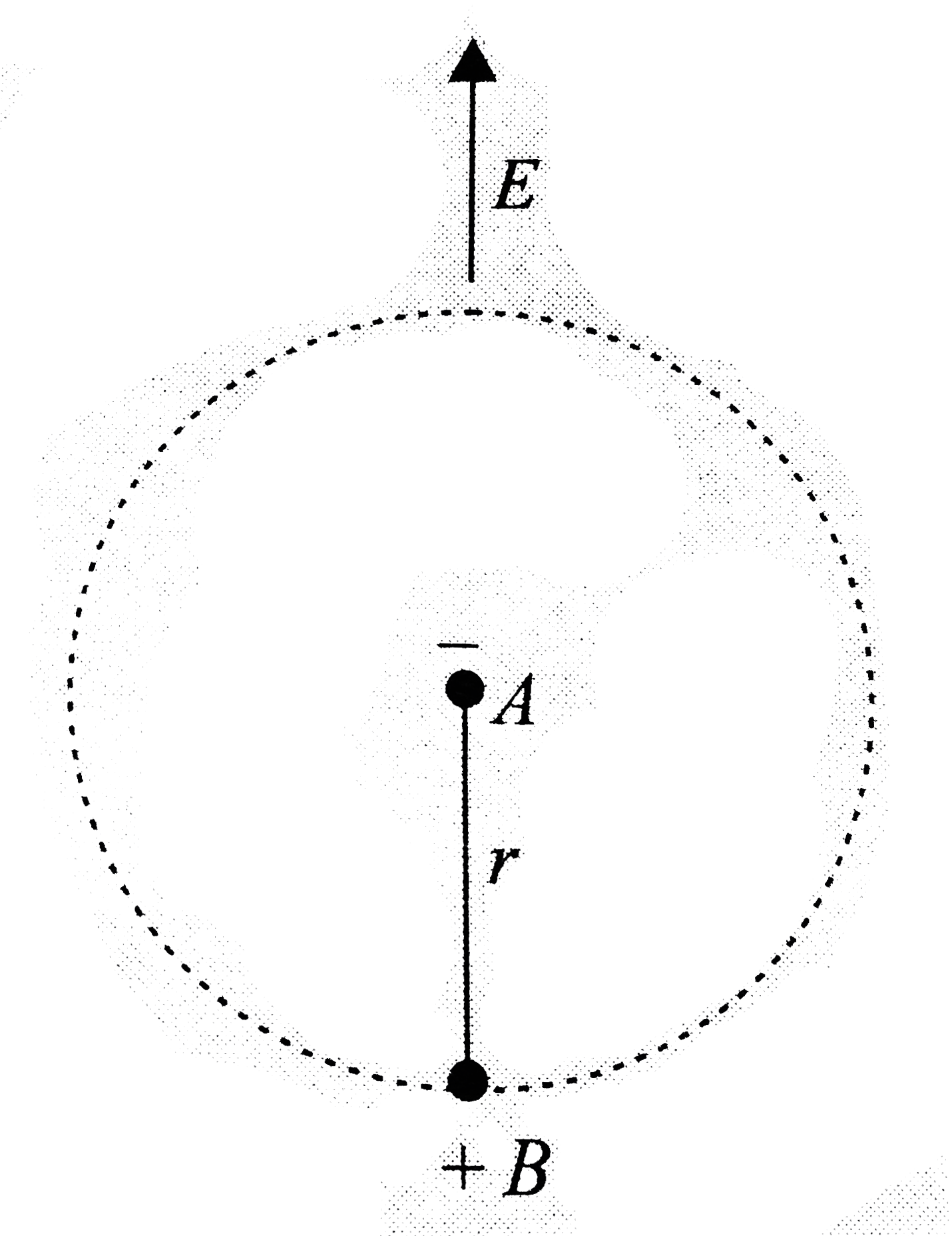 .
.
Let us analyse the forces acting on charge B.
(i) Force of attraction between charges An and B
F1=14πε0q1q2r2
=9×109×(15518×10−6)(100×10−6)(0.5)2=31N
(acts in radial direction, always directed toward the center)
(ii) Force due to electric field
F2=q2E
=(100×10−6)×(1.1×105)
=11N (directed vertically upward)
(iii) Weight W=mg=0.5×10=5N (vertically downward)
(iv) Tension T in the string, acting downward.
Since F1 is always directed toward the center, the critical position depends on F2 and W. their resultant is 6 N (vertically upward). At the critical position, this resultant must be directed toward the center. hence, the tension in the thread is minimum when particle B us at the lowest position. Considering free body diagram at this position, we have
mv20r=F1+F2+T−W
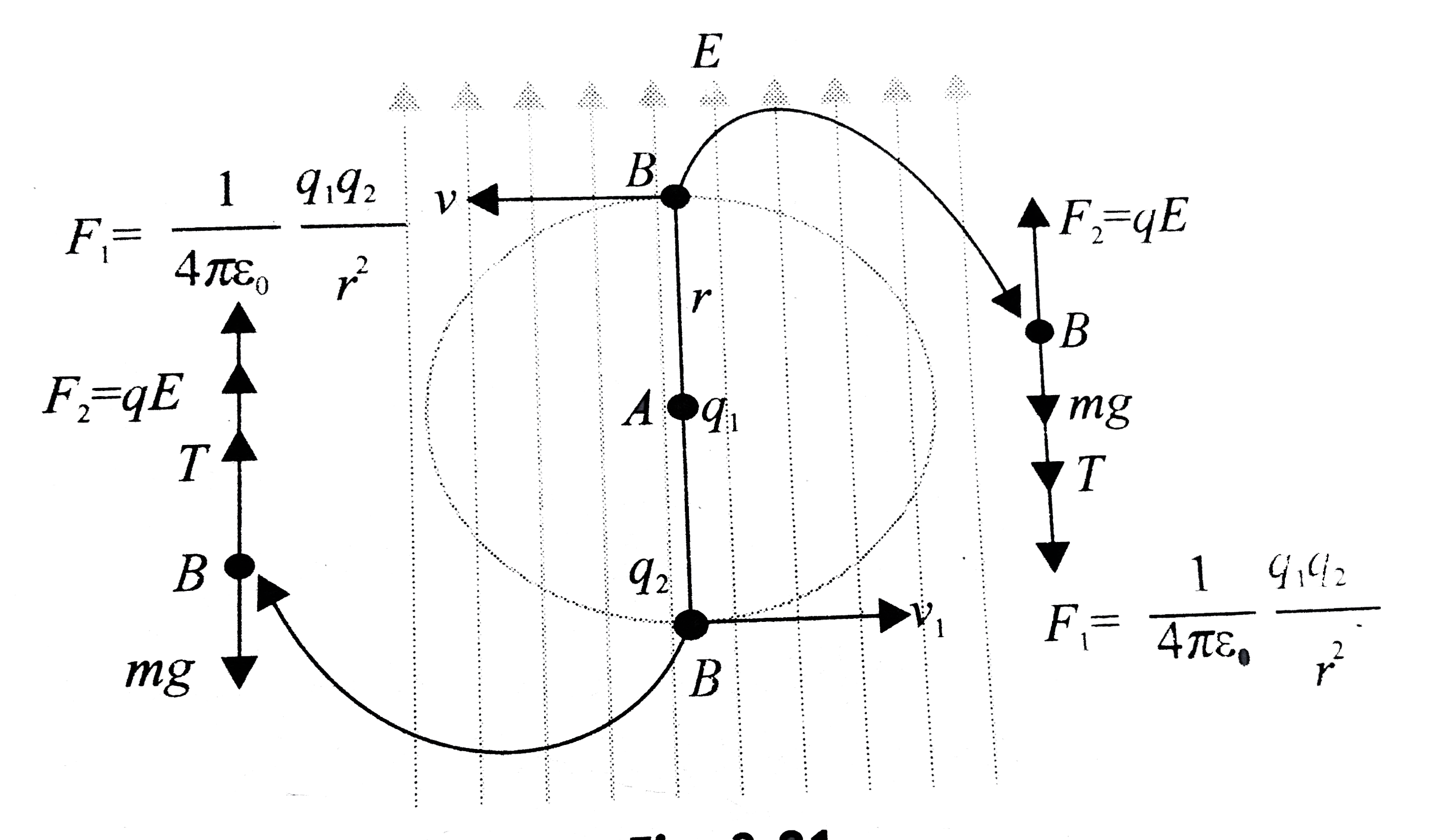 .
.
But for T=0, we get v0=√37ms−1. When the particle moves from the lowest to the hight position, work is done on it by force F2 , however, gravitational potential energy increases and no work is done by F1 . Let minimum velocity required at the highest point be v. Using work energy theorem between the lowest and highest position on circle,
Wtotal=ΔK
or Welectric+Wgravity=ΔKorqE(2r)−mg(2r)=12mv2−12mv20
which gives v=√16ms−1.
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC POTENTIALEXERCISE - Examples9videos
ELECTRIC POTENTIAL
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC POTENTIALEXERCISE - Exercise 3.123videos
ELECTRIC POTENTIAL
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC FLUX AND GAUSS LAWEXERCISE - MCQ s38videos
ELECTRIC FLUX AND GAUSS LAW
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRICAL MEASURING INSTRUMENTSEXERCISE - M.C.Q2videos
ELECTRICAL MEASURING INSTRUMENTS
Similar Questions
A small sphere of mass m=0.5kg carrying a positive charge q=110μC is connected with a light, flexible, and inextensible string of length of length r=60cm and whirled in a vertical circle. If a vertically upward electric field of strength E=105NC−1 exists in the space, calculate the minimum velocity of the sphere required at the highest point so that it may just complete the circle (g=10ms−2).
View SolutionA small sphere of mass m=0.6kg carrying a positive charge q=80μC is connected with a light, flexible, and inextensible string of length r=30cm and whirled in a vertical circle. If a horizontal rightward electric field of strength E=105NC−1 exists in the space, calculate the minimum velocity of the sphere required at the highest point so that it may just complete the circle (g=10ms−2).
View SolutionA particle is fastened at the end of a string and whirled in a vertical circle with the other end of the string being fixed. The motion of the particle is
View SolutionTwo small balls A and B of positive charge Q each and masses m and 2m, respectively, are connected by a nonconducting light rod of length L. This system is released in a uniform electric field of strength E as shown. Just after the release (assume no other force acts on the system)
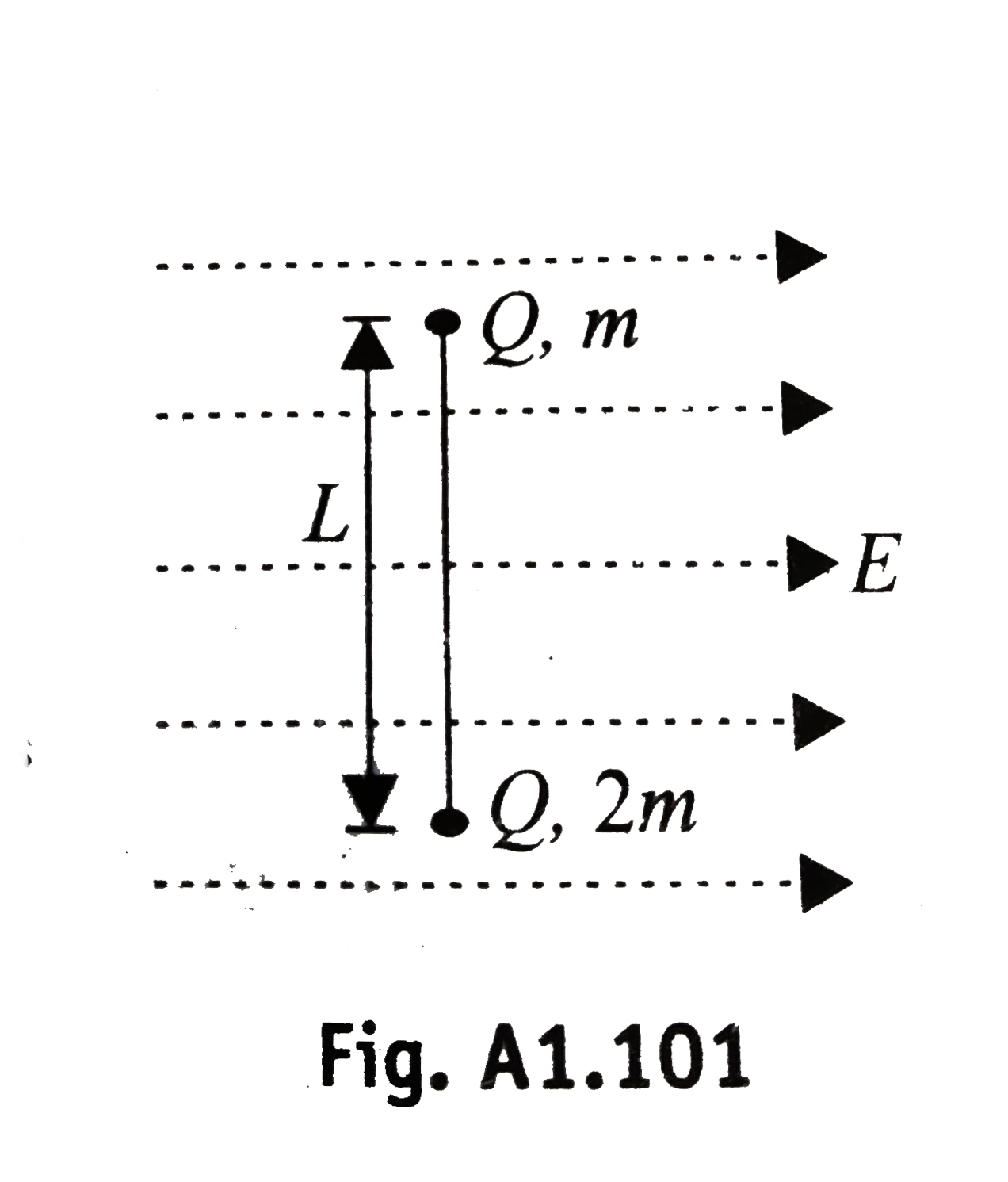 View Solution
View SolutionA particle is rotated in a vertical circle by connecting it to a string of length l and keeping the other end of the string fixed. The minimum speed of the particle when the string is horizontal for which the particle will complete the circle is
View SolutionA particle of mass m and charge Q is attached to a string of length l. It is whirled in a vertical circle in the region of an electric field E as shown in the figure-5.105.What is the speed given to the particle at the point B,so that tension in the string when the particle is at A is ten times the weight of the particle?
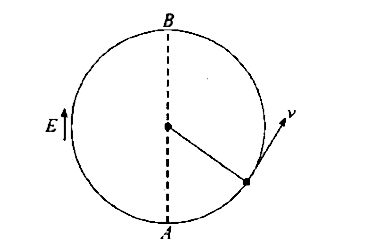 View Solution
View SolutionA particle of mass m and charge q is thrown in a region where uniform gravitational field and electric field are present. The path of particle:
View SolutionTwo point charges Q1=400μCand Q2=100μC are kept fixed, 60 cm apart in vacuum. Find intensity of the electric field at midpoint of the line joining Q1 and Q2.
View SolutionThree charges q1=1μC,q2=2μC and q3=3μC are placed on the vertices of an equilateral triangle of side 1.0 m. Find the net electric force acting on charge q1
 View Solution
View SolutionA charged particle of mass 5×10−5kg is held stationary in space by placing it in an electric field of strength 107NC−1 directed vertically downwards. The charge on the particle is
View Solution

