An electron is fired directly towards the center of a large metal plate that has excess negative charge with surface charge density =2.0×10−6C/m2. If the initial kinetic energy of electron is 100 eV and if it is to stop due to repulsion just as it reaches the plate, how far from the plate must it be fired ?
0.44 mm
0.20 mm
1 mm
0.30 mm
The correct Answer is:a
To solve the problem, we will follow these steps:
Step 1: Understand the Problem
We have an electron that is fired towards a negatively charged metal plate. The initial kinetic energy of the electron is given as 100 eV, and the surface charge density of the plate is σ=2.0×10−6C/m2. We need to find the distance from which the electron must be fired so that it stops just as it reaches the plate.
Step 2: Convert Kinetic Energy to Joules
The initial kinetic energy (KE) of the electron is given in electron volts (eV). We need to convert this to joules (J) using the conversion factor 1eV=1.6×10−19J.
KE=100eV=100×1.6×10−19J=1.6×10−17J
Step 3: Calculate the Electric Field (E) due to the Plate
The electric field E created by an infinite plane sheet with surface charge density σ is given by:
E=σϵ0
where ϵ0 (the permittivity of free space) is approximately 8.85×10−12C2/N m2.
Substituting the values:
E=2.0×10−68.85×10−12≈2.26×105N/C
Step 4: Relate Work Done to Change in Kinetic Energy
According to the work-energy theorem, the work done by the electric field on the electron as it moves towards the plate is equal to the change in kinetic energy. Since the electron comes to a stop, the work done is equal to the initial kinetic energy:
W=KE=F⋅s
where F is the force on the electron and s is the distance from which it is fired.
Step 5: Calculate the Force (F) on the Electron
The force F on the electron due to the electric field is given by:
F=qE
where q is the charge of the electron, q=−1.6×10−19C. Thus,
F=−1.6×10−19×2.26×105≈−3.62×10−14N
Step 6: Substitute into the Work Equation
Now substituting F into the work equation:
1.6×10−17=3.62×10−14⋅s
Step 7: Solve for Distance (s)
Rearranging the equation to find s:
s=1.6×10−173.62×10−14≈4.43×10−4m
Step 8: Convert to Millimeters
To convert meters to millimeters, we multiply by 1000:
s≈4.43×10−4m×1000=0.443mm
Final Answer
The distance from which the electron must be fired is approximately 0.44mm.
---
We have an electron that is fired towards a negatively charged metal plate. The initial kinetic energy of the electron is given as 100 eV, and the surface charge density of the plate is σ=2.0×10−6C/m2. We need to find the distance from which the electron must be fired so that it stops just as it reaches the plate.
The initial kinetic energy (KE) of the electron is given in electron volts (eV). We need to convert this to joules (J) using the conversion factor 1eV=1.6×10−19J.
The electric field E created by an infinite plane sheet with surface charge density σ is given by:
According to the work-energy theorem, the work done by the electric field on the electron as it moves towards the plate is equal to the change in kinetic energy. Since the electron comes to a stop, the work done is equal to the initial kinetic energy:
The force F on the electron due to the electric field is given by:
Now substituting F into the work equation:
Rearranging the equation to find s:
To convert meters to millimeters, we multiply by 1000:
The distance from which the electron must be fired is approximately 0.44mm.
Topper's Solved these Questions
- ELECTRIC POTENTIALBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC POTENTIALEXERCISE - Multiple Correct
10 Videos
- ELECTRIC POTENTIALBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC POTENTIALEXERCISE - Comprehension
31 Videos
- ELECTRIC POTENTIALBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC POTENTIALEXERCISE - Subjective
28 Videos
- ELECTRIC FLUX AND GAUSS LAWBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC FLUX AND GAUSS LAWEXERCISE - MCQ s
38 Videos
- ELECTRICAL MEASURING INSTRUMENTSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRICAL MEASURING INSTRUMENTSEXERCISE - M.C.Q
2 Videos
Similar Questions
Two parallel large thin metal sheets have equal surface charge densities (σ=26.4×10−12C/m2) of opposite signs. The electric field between these sheets is
View SolutionFrom what distance should a 100 eV electron be fired towards a large metal plate having a surface charge of −2.0×10−6Cm−2, so that it just fails to strike the plate ?
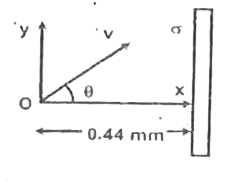
View SolutionAn electron is projected with a velocity of 1.186×107m/s at an angle θ with the x-axis, towards a large metallic plate kept 0.44 mm away from the electron. The plate has a surface charge density −2×10−6C/m2. Find the minimum value of θ, for which it fails to strike the plate.
View SolutionA large conducting plane has a surface charge density 1.0x10−4Cm−2 . Find the electrostatic energy stored in a cubical volume of edge 1 cm in the front plane.
View SolutionA charged partical having a charge of −2.0×10−6C is placed close to a nonconducting plate having a surface charge density 4.0 xx 10^(-6) C m^(-2). Fine the force of attraction between the particle and the plate.
View SolutionA light of intensity 16 mW and energy of each photon 10 eV incident on a metal plate of work function 5 eV and area 10−4m2 then find the maximum kinetic energy of emitted electrons and the number of photoelectrons emitted per second if photon efficiency is 10%.
View SolutionA small piece of cesium metal ϕ=1.9eV is kept at a distance of 20 cm form a large metal plate having a charge density of 1.0×10−9Cm−2 on the surface facing the cesium piece. A monochromatic light of wavelength 400nm is incident on the cesium piece. Find the minimum and the maximum kinetic energy of the photoelectrons reaching the large metal plate. Neglect any change in electric field due to the small piece of cesium present.
View SolutionTwo large thin metal plates are parallel and close to each other. On their inner faces, the plates have surface charge densities of opposite signs and magnitude 27×10−22Cm−2. The electric field →E in region II in between the plates is

View SolutionTwo large this metal plates are parallel and close to each other. On their inner faces, the plates have surface charge densities of opposite signs and magnitude 17.0×10−22C/m2. What is →E : (a) In the outer region of the first plate. (b) In the outer region of the secound plate, and (c) Between the plates ? See Fig.
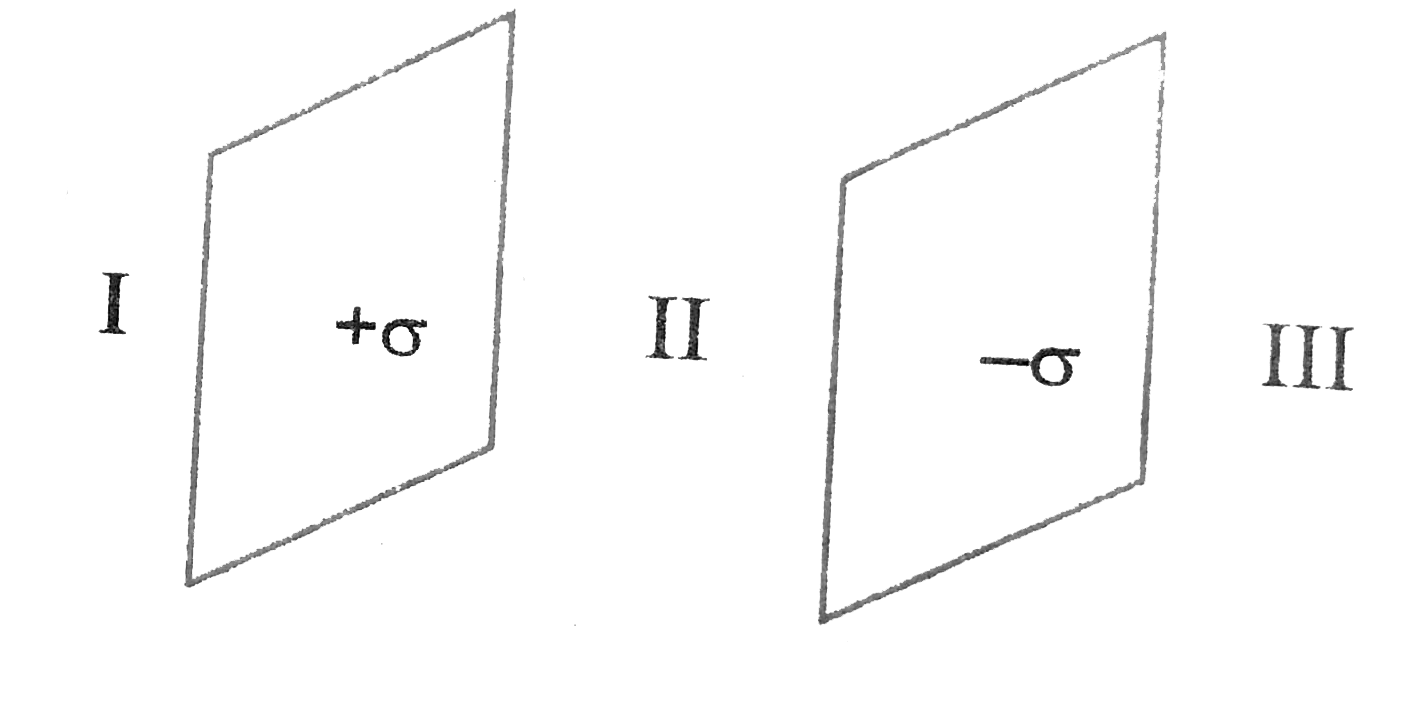
View SolutionTwo large, thin metal plates are parallel and close to each other. On their inner faces, the plates have surface charge densities of opposite signs and of magnitude 17.0×10−22C/m2. What is E : between the plates?
View Solution
