A charged partical having a charge of is placed close to a nonconducting plate having a surface charge density 4.0 xx 10^(-6) C m^(-2). Fine the force of attraction between the particle and the plate.
To find the force of attraction between a charged particle and a non-conducting plate with a given surface charge density, we can follow these steps:
Step 1: Identify the Given Values
- Charge of the particle, q=−2.0×10−6C
- Surface charge density of the plate, σ=4.0×10−6C/m2
Step 2: Calculate the Electric Field (E) due to the Plate
For an infinite non-conducting sheet with surface charge density σ, the electric field E produced is given by the formula:
E=σ2ε0
where ε0 (the permittivity of free space) is approximately 8.85×10−12C2/N m2.
Substituting the values:
E=4.0×10−62×8.85×10−12
Step 3: Calculate the Electric Field Value
Calculating the denominator:
2×8.85×10−12=1.77×10−11C2/N m2
Now, substituting back into the equation for E:
E=4.0×10−61.77×10−11≈226.56N/C
Step 4: Calculate the Force (F) on the Charged Particle
The force F acting on the charged particle in the electric field is given by:
F=qE
Substituting the values:
F=(−2.0×10−6)×(226.56)
Step 5: Calculate the Force Value
Calculating the force:
F≈−4.53×10−4N
The negative sign indicates that the force is attractive (since the charge of the particle is negative and the electric field direction is away from the plate).
Step 6: Final Result
The magnitude of the force of attraction between the particle and the plate is:
F≈0.45N
Summary
The force of attraction between the charged particle and the plate is approximately 0.45N.
---
- Charge of the particle, q=−2.0×10−6C
- Surface charge density of the plate, σ=4.0×10−6C/m2
For an infinite non-conducting sheet with surface charge density σ, the electric field E produced is given by the formula:
E=σ2ε0
where ε0 (the permittivity of free space) is approximately 8.85×10−12C2/N m2.
E=4.0×10−62×8.85×10−12
Calculating the denominator:
2×8.85×10−12=1.77×10−11C2/N m2
Now, substituting back into the equation for E:
E=4.0×10−61.77×10−11≈226.56N/C
The force F acting on the charged particle in the electric field is given by:
F=qE
Substituting the values:
F=(−2.0×10−6)×(226.56)
Calculating the force:
F≈−4.53×10−4N
The negative sign indicates that the force is attractive (since the charge of the particle is negative and the electric field direction is away from the plate).
The magnitude of the force of attraction between the particle and the plate is:
F≈0.45N
The force of attraction between the charged particle and the plate is approximately 0.45N.
Topper's Solved these Questions
- BOOK - HC VERMA ENGLISHCHAPTER - GAUSS LAWEXERCISE - Short Question7videos
GAUSS LAW
- BOOK - HC VERMA ENGLISHCHAPTER - GAUSS LAWEXERCISE - Objective 28videos
GAUSS LAW
- BOOK - HC VERMA ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Exercise8videos
ELECTROMAGNETIC WAVES
- BOOK - HC VERMA ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - Question For short Answer18videos
GEOMETRICAL OPTICS
Similar Questions
An infinite nonconducting sheet of charge has a surface charge density of 107C/m2. The separation between two equipotential surfaces near the whose potential differ by 5V is
View SolutionAn electric dipole consists of charges ±2.0×108C separated by a distance of 2.0×10−3 m. It is placed near a long ilne charge of linear charge density 4.0×10−4Cm−1 as shown in figure (30-W4), Such thet the negative charge is at a distance of 2.0 cm from the line charge. Find the force acting on the dipole.
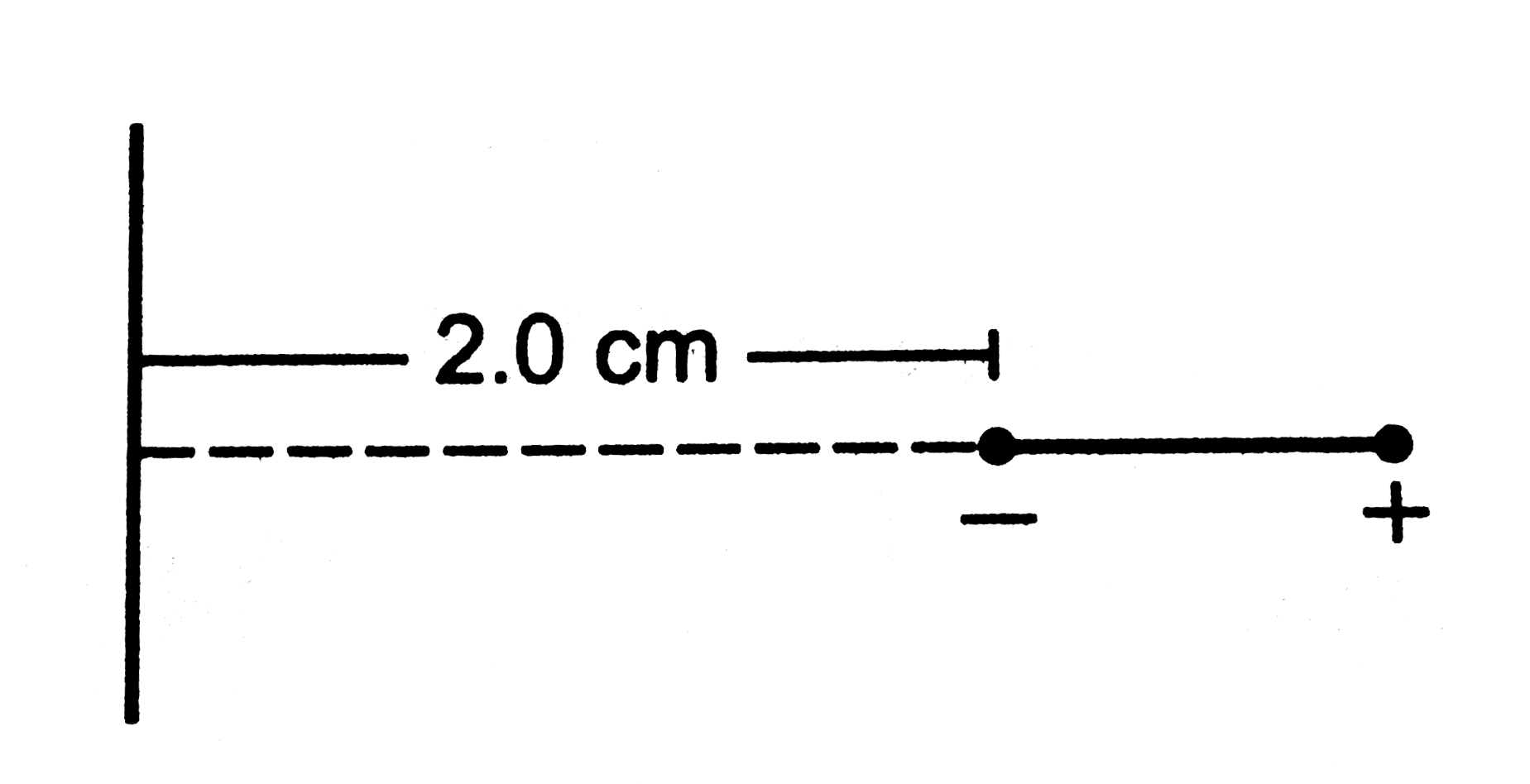 View Solution
View SolutionAn electric dipole consists of charges ±2.0×10−8C separated by a distance of 2.0×10−3 m. It is placed near a long line charge of linear charge density 4.0×10−4Cm−1 as shown in figure (30-W4), Such that the negative charge is at a distance of 2.0 cm from the line charge. Find the force acting on the dipole.
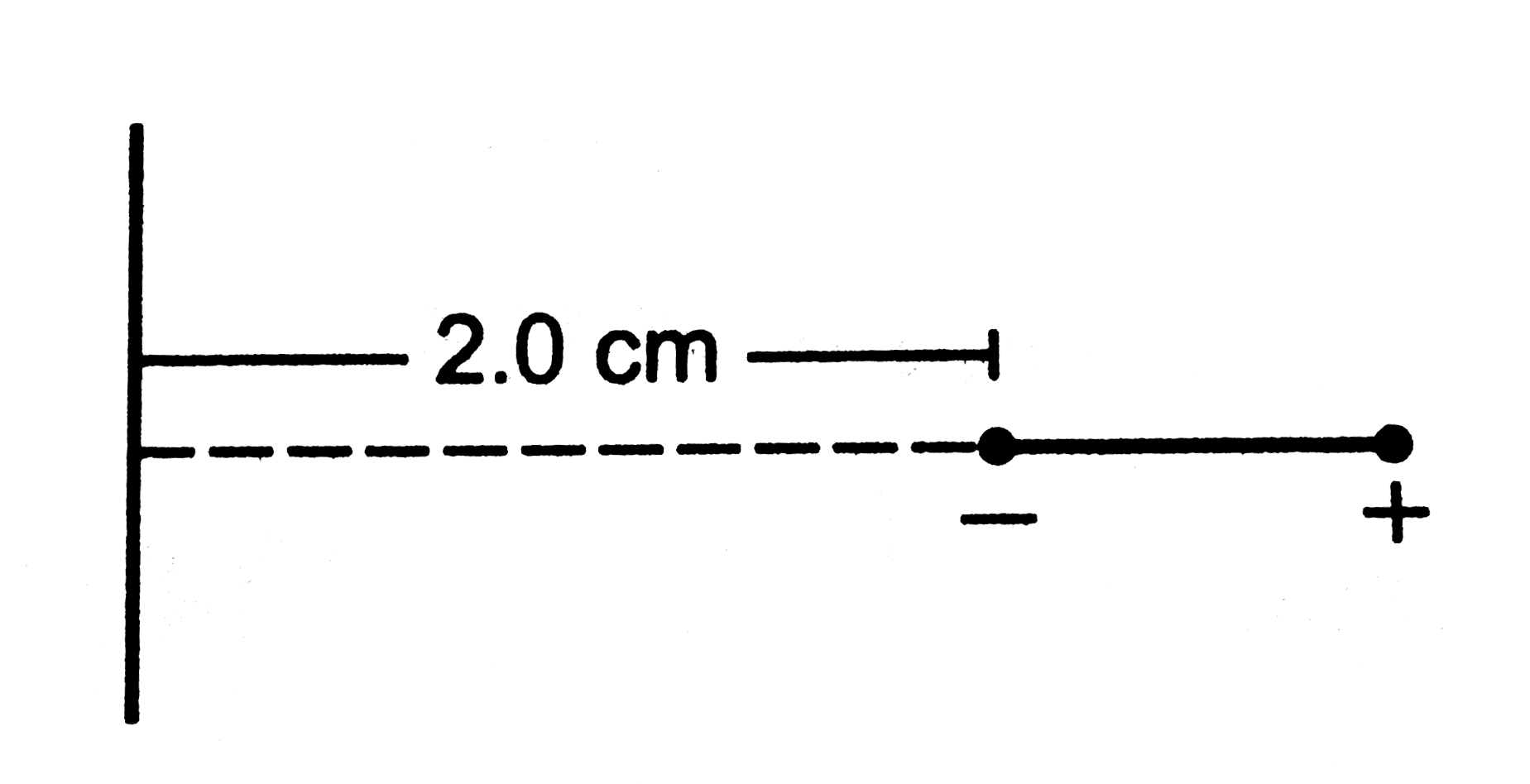 View Solution
View SolutionFrom what distance should a 100 eV electron be fired towards a large metal plate having a surface charge of −2.0×10−6Cm−2, so that it just fails to strike the plate ?
View SolutionAn electric dipole consists of charges ±2.0×10−8 C separated by distance of ±2.0×10−3m. It is placed at a distance of 6 cm from a line charge of linear charge density 4.0×10−4Cm−1 as shown in figure such that the dipole makes an angle of θ=60∘ with line AB. Find the force acting on the dipole.
 View Solution
View SolutionWhat is the force between two small charged of 2×10−7 C placed 30 cm apart in air?
View SolutionTwo charged particles, having equal charges of 2.0×10−5C each, are brought from infinity to within a separation of 10 cm. Find the increase in the electric potential energy during the process.
View SolutionFind the magnitude of the electric field at a point 4 cm away from a line charge of density 2×10−6Cm−1.
View SolutionA particle of mass 5×10−6g is kept over a large horizantal sheet of charge of denisity 4.0×10−6Cm−2 (Figure 30-W5). What charge should be given to this partical so that if released, it does not fall down? How many electrons are to be removed to give this charge? How much mass is decreased due to the removal of these electrons?
 View Solution
View SolutionTwo parallel large thin metal sheets have equal surface charge densities (σ=26.4×10−12C/m2) of opposite signs. The electric field between these sheets is
View Solution

