If you have several 2.0μF capacitrors, each capable of withstanding 200V without breakdown, how would you assemble a combination that has an equivalent capacitance of
a. 0.4μF
b. 1.2μF each with standing 1000V?
To solve the problem, we need to find the arrangements of capacitors that will give us the desired equivalent capacitance while also ensuring that the voltage rating is met.
Part a: Achieving an Equivalent Capacitance of 0.4 µF
1. Understanding Series Connection: Since we need an equivalent capacitance that is less than the capacitance of each capacitor (2.0 µF), we will connect the capacitors in series. The formula for the equivalent capacitance Ceq in series is given by:
1Ceq=1C1+1C2+…+1Cn
2. Substituting Values: For n capacitors of 2.0μF:
1Ceq=n2.0μF
We want Ceq=0.4μF. Therefore:
10.4=n2.0
3. Calculating n:
10.4=2.5(taking the reciprocal)
2.5=n2.0⟹n=2.5×2.0=5
Thus, we need 5 capacitors connected in series to achieve an equivalent capacitance of 0.4μF.
Part b: Achieving an Equivalent Capacitance of 1.2 µF withstanding 1000 V
1. Understanding Parallel Connection: Now, we need to achieve 1.2μF. Since 1.2μF is greater than 0.4μF, we can use the 0.4μF we just calculated and connect it in parallel with additional capacitors.
2. Using the Series Result: We have already established that connecting 5 capacitors in series gives us 0.4μF.
3. Finding the Number of Parallel Capacitors: To achieve 1.2μF:
Ceq=C1+C2+…+Cn
If we connect n capacitors of 0.4μF in parallel:
Ceq=0.4μF×n
We want:
0.4μF×n=1.2μF
4. Calculating n:
n=1.20.4=3
Thus, we need 3 sets of 5 capacitors (each set in series) connected in parallel to achieve an equivalent capacitance of 1.2μF.
Summary of the Solution
- For 0.4 µF: Connect 5 capacitors in series.
- For 1.2 µF: Connect 3 sets of 5 capacitors in series in parallel.
1Ceq=1C1+1C2+…+1Cn
1Ceq=n2.0μF
We want Ceq=0.4μF. Therefore:
10.4=n2.0
10.4=2.5(taking the reciprocal)
2.5=n2.0⟹n=2.5×2.0=5
Thus, we need 5 capacitors connected in series to achieve an equivalent capacitance of 0.4μF.
Ceq=C1+C2+…+Cn
If we connect n capacitors of 0.4μF in parallel:
Ceq=0.4μF×n
We want:
0.4μF×n=1.2μF
n=1.20.4=3
Thus, we need 3 sets of 5 capacitors (each set in series) connected in parallel to achieve an equivalent capacitance of 1.2μF.
- For 0.4 µF: Connect 5 capacitors in series.
- For 1.2 µF: Connect 3 sets of 5 capacitors in series in parallel.
Topper's Solved these Questions
- CAPACITOR AND CAPACITANCEBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CAPACITOR AND CAPACITANCEEXERCISE - Subjective
24 Videos
- CAPACITOR AND CAPACITANCEBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CAPACITOR AND CAPACITANCEEXERCISE - Single Correct
49 Videos
- CAPACITOR AND CAPACITANCEBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CAPACITOR AND CAPACITANCEEXERCISE - Exercise 4.1
13 Videos
- ATOMIC PHYSICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ATOMIC PHYSICSEXERCISE - ddp.4.3
15 Videos
- CENGAGE PHYSICS DPPBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENGAGE PHYSICS DPPEXERCISE - subjective type
51 Videos
Similar Questions
Several 10pF capacitors are given, each capable of withstanding 100V. How would you construct :
(a) a unit possessing a capacitance of 2pF and capable of withstanding 500V?
(b) a unit possessing a capacitance of 20pF and capable of withstanding 300V?
View SolutionFind the equivalent capacitance between points A and B. Capacitance of each capacitor is 2μF.
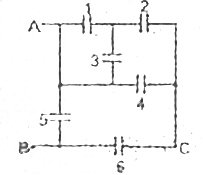
View SolutionThree capacitors of capacitances 1μF,2μFand4μF are connected first in a series combination, and then in parallel combination. The ratio of their equivalent capacitances will be
View SolutionEach capacitor shown in the figure is 2μF. Then the equivalent capacitance between points A and B is

View SolutionSeven capacitors each of capacitance 2μF are to be connected in a configuration to obtain an effective capacitance of (1011)μF. Which of the combination (s) shown in figure will achieve the desired result?
View SolutionSeven capacitors, each a of a cpacitance 2μF, are to be connected in a configuration to obatin an effective capacitance of (1613)μF. Which of the combinations, shown in figure below, will achieve the desired value ?
View SolutionTo form a capacitor equivalent of 16μF, with breakdown voltage of 1000V, how many minimum number of capacitance marked 8μF,250V are required?
View SolutionAn infinite ladder is constructed by connecting several sections of2μF,4μF capacitor combinations as shown in figure . It is terminated by a capacitor of capacitance C . What value should be chosen for C, such that the equivalent capacitance of the number of sections in between ?
View SolutionSix identical capacitors each of capacitance 2μF are connected as shown below. The equivalent capacitance between the points A and B is
View SolutionIn each capacitance C1 is 6.0μF, and each capacitance C2 is 4.0μF.
 .
.
The equivalent capacitance of the netwok between ponts a and b is.
View Solution

